3. Вычисление определителя третьего порядка разложением по первой строке:

(это одно из свойств определителя, но пока мы будем работать с этим свойством, не вникая в его происхождение)

= a₁₁ a₂₂ a₃₃ + a₁₂ a₂₃ a₃₁ + a₁₃ a₂₁ a₃₂ - a₁₃ a₂₂ a₃₁ - a₁₂ a₂₁ a₃₃ - a₁₁ a₂₃ a₃₂

• Упражнение 1. Вычисление определителей III порядка

Создать квадратную матрицу размером 3х3.

Вычислить определитель матрицы B

1)по правилу Саррюса, обращаясь через индексы к элементам массива

2)разложить по первой строке, обращаясь через индексы к элементам массива

3)сделать проверку пунктов 1 и 2, обращаясь к стандартной функции det()

2. Векторное произведение и его геометрическая иллюстрация.

   1. Определение векторного произведения

Три некомпланарных вектора образуютправую тройку, если они удовлетворяют следующему условию: если смотреть из конца вектора тократчайший поворот от вектора к векторуосуществляется против часовой стрелки. Иначе–левая тройка. Система координат – правая, если базисные векторы образуют правую тройку, илевая, если – левая тройка.

Векторным произведением векторов и (обозначаетсяили) называется вектортакой, что выполняются условия:

1. 

2. (длина этого вектора равна площади параллелограмма, построенного на векторах и );

3. векторы образуют правую тройку

Замечание.Очевидно, условия (1) - (3) определяют вектороднозначно. Условие (3), конечно, относится к случаю, когда векторыи неколлинеарны. Если векторыи , то условие (2) показывает, что

Свойства векторного произведения векторов:

1. (антикоммутативность);

2. (дистрибутивность);

3. _{(λ – любое вещественное число)}.

4. 

5. Условие коллинеарности векторов:

коллинеарны

2. Выражение векторного произведения через координаты векторов

Пусть – векторы, заданные своими координатами впрямоугольной системе координат, и–правая тройка. Тогда:

Если разложить определитель по первой строке, то получится:

Или, что то же самое:

Это свойство очень пригодится нам в дальнешем.

Упражнение 2. Найти векторное произведение векторов

Найти векторное произведение векторов 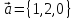ис помощью определителя третьего порядка см формулу (8) и проверить решение стандартной функциейcross(a,b). Вычислить определитель полученной матрицы разложением по первой строке, обращаясь индексами к элементам матрицы.Проверить себя в тетради и стандартными функциями det() и cross(a,b)

3. Геометрическая иллюстрация векторного произведения.

Найти векторное произведение векторов 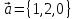и. Изобразить все данные и результат. Первый вектор изобразить синим, второй зеленым, результат красным. Сделать выводы: как связаны определение векторного произведения и то, что мы получили на рисунке.

%Задаем векторы

a=[1,2,0];b=[2,1,0];

% Находим векторное произведение

c=cross(a,b)

% Нашли векторное произведение.

% Это будет вектор с координатами c=(0,0,-3)

% офоррмляем график, задаем коорд оси

grid on, holdon, axissquare

line([-5 0 0;5 0 0], [0 -5 0;0 5 0],[0 0 -5;0 0 5],'Color','black')

% первый вектор, по умолчанию цвет - синий

line([0 1],[0,2],'LineWidth',4)

% конец вектора, по умолчанию цвет синий

plot3(1,2,0,'>','LineWidth',4)

% второй вектор

line([0 2],[0,1],'Color','green','LineWidth',4).

plot3(2,1,0,'>g','LineWidth',4)

% результат векторного произведения c=(0,0,-3)

line([0 0],[0,0],[0 -3],'Color','red','LineWidth',4)

plot3(0,0,-3,'>r','LineWidth',4) % конец вектора

plot3(5,0,0,'<k','LineWidth',2) % направление оси 0X

plot3(0,5,0,'>k','LineWidth',2) %направление оси 0Y

plot3(0,0,5,'^k','LineWidth',2) % направление оси 0Z

text(5,-0.5,0.8,'X') % подпись оси 0X

text(-0.5,5,0.8,'Y') % подпись оси 0X

text(-0.5,-1,5,'Z') % подпись оси 0Z

Как только появится графическое окно “Figure1”, с помощью круговой стрелочки “Rotate3D” (cм. панель инструментов), разворачиваем плоскую картинку в объемную и разворачиваем изображение.

Рис. 1

Выводы: Синий вектор,зеленый вектор 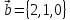икрасный вектор образуют правую тройку. Векторперпендикуляренплоскости векторов и.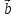

Изобразим параллелограмм, натянутый на векторы 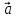и.

Найдем длину вектора 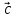-длина вектораравна площади параллелограмма сторонами которого являются векторыи.

Изобразим плоскость параллелограмма:

Рис. 2.

% соединим штриховкой зеленый вектор – сторону параллелограмма

% и параллельную ей сторону параллелограмма

%каждый отрезок имеет начало в точке (x1, y1), конец в точке (x2,y2)

% смотрим на зеленый вектор-отрезок, задаем диапазон изменения

% начальных координат абсцисс x1

x1=0.1:0.1:1.9;

% y1 связан с x1 прямой y=x/2, поэтому

y1=x1/2;

% координаты (x2,y2) поучаются сдвигом (x1,y1) на вектор a

% (x2,y2)=(x1,y1)+a=(x1+1,y1+2)

% операция x1+1 осуществит прибавление единицы

% к каждому элементу массива x1

x2=x1+1; y2=y1+2;

line([x1; x2],[y1; y2],'LineWidth',4,'Color',[0.8 0.1 0.7])

Получаем

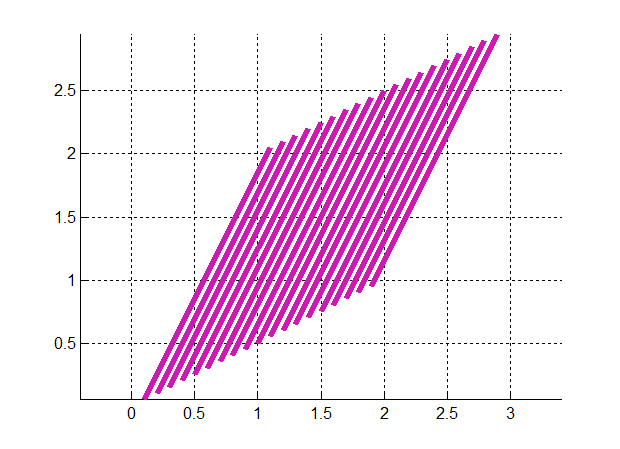
Рис. 3.

Соеденив два куска программы получим:

Рис. 4

Чтобы изобразить плоскость параллелограмма, можно также воспользоваться встроенной функцией fill(). Ознакомьтесь с форматом входных аргументов в документации.

>> fill([0 2 3 1], [0 1 3 2], 'm')

Рис. 5