
- •Порядок выполнения.
- •ОпределителиIIиIiIпорядков.
- •Определитель второго порядка
- •Вычисление определителейIIпорядка
- •Определитель третьего порядка
- •Вычисление определителя третьего порядка разложением по первой строке:
- •Упражнение 1. Вычисление определителей III порядка
- •Векторное произведение и его геометрическая иллюстрация.
- •Определение векторного произведения
- •Выражение векторного произведения через координаты векторов
- •Упражнение 2. Найти векторное произведение векторов
- •Геометрическая иллюстрация векторного произведения.
- •Упражнение 3. Вычислить площадь треугольника с помощью векторного произведения
- •Прямая на плоскости.
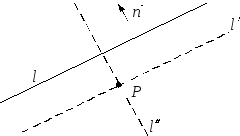
- •Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному вектору.
- •Построение уравнения прямой, проходящей через заданную точку перпендикулярно данному вектору.
- •Часть 1.
- •Часть 2
- •Часть 3.
- •Уравнение прямой линии, проходящей через данную точку в заданном направлении. Каноническое уравнение прямой на плоскости.
- •Упражнение 4. Каноническое уравнение прямой.
- •Уравнение прямой, проходящей через две точки.
- •Упражнение 5. Уравнение прямой, проходящей через две точки.
- •Параметрическое задание прямой.
- •Упражнение 6. Параметрическое задание прямой.
- •Упражнение 8. Общее уравнение прямой.
- •Создание м-файла.
- •Упражнение 9. М-функция для построения двух прямых линий.
- •Система двух уравнений первой степени с двумя неизвестными и их геометрическая интерпретация.
- •Упражнение.10. Геометрическая интерпретация системы двух уравнений первой степени с двумя неизвестными.
- •Уравнения плоскости в пространстве.
- •Различные уравнения плоскости.
- •Построение плоскости графическим средствами matlab.
- •Пример. 1. Общее уравнение плоскости. Функция meshgrid.
- •Пример 2. Построение плоскость по общему уравнению с помощью функций mesh(),surf(), surfl().
- •Упражнение 11. Уравнение плоскости в отрезках.
- •Прямая в пространстве.
- •Параметрическое и каноническое уравнение прямой в пространстве.
- •Пример.3. Построение прямой в пространстве, заданной параметрически.
- •Общее уравнение прямой в пространстве.
- •Упражнение 12. Общее уравнение прямой в пространстве.
- •Система двух и трех уравнений первой степени с тремя неизвестными и их геометрическая интерпретация.
- •Система двух однородных уравнений с тремя неизвестными
- •Упражнение 13. Система двух однородных уравнений с тремя неизвестными
- •Система трех уравнений первой степени с тремя неизвестными
- •Упражнение. 14. Система двух уравнений первой степени с двумя неизвестными.
- •Задание для самостоятельной работы
- •Контрольные вопросы.
- •Контрольное мероприятие № 2. Защита л.1.3.
- •Часть 2 Работа с системой matlab
- •Индивидуальные задания № 2 Линейные геометрические объекты.
- •Список рекомендуемой литературы
Часть 2 Работа с системой matlab
1. Сколько будет узловых точек? Изобразить результат выполнения функции.
Цвет, вид маркера указать словами.
А) plot([1 2],[3 5],'*b-') (Не путать с line)
Б) x=[-3 0 3];
y1=2*x+1; y2=3*x+5; plot(x,y1,'r--',x,y2,'g')
2. Дано
A = 3; B = 4; C = -4; D = -12;
x = -1:1:1; y = 0:0.5:1;
[X,Y]=meshgrid(x,y);
Z = (-A*X-B*Y-D)/C;
plot3(X,Y,Z,'ok','MarkerSize',8), box on, hold on
xlabel('x'), ylabel('y'), zlabel('z')
title('3x + 4y - 4z - 12 = 0')
surf(X,Y,Z)
Составить таблицы для xи у,XиY, и дляZ.
Описать, что делают функции meshgrid,plot3 иsurf.
(Читай help и/или Кривилёва стр 153,154). Можно и нужно принести калькулятор.
Образец билета
|
1. Вывод общего уравнения прямой на плоскости. Векторное уравнение прямой. Нормальный вектор прямой. |
2. Каноническое и параметрическое уравнение прямой на плоскости. Направляющий вектор. |
|
Опишите, что делает каждая строчка данной программы. A = 3; B = 4; C = -4; D = -12; x = -1:1:1; y = 0:0.5:1; [X,Y]=meshgrid(x,y); Z = (-A*X-B*Y-D)/C; plot3(X,Y,Z,'ok','MarkerSize',8), box on, hold on xlabel('x'),ylabel('y'), zlabel('z') title('3x + 4y - 4z - 12 = 0') surf(X,Y,Z)
|
Опишите и изобразите на листочке, что делает данная строчка. plot([-3 4],[0 5],'oy-') Опишите и изобразите на листочке, что делает данная программа x=[-3 0] y1=2*x+1; y2=3*x+5; plot(x,y1,'b--',x,y2,'g')
|
Индивидуальные задания № 2 Линейные геометрические объекты.
Задания разного уровня сложности. Задачи необходимо иллюстрировать в MATLAB
При построении соблюдать одинаковый масштаб по осям координат. Взаимно перпендикулярные прямые должны оставаться перпендикулярными.
1. Решить систему по формулам Крамера, используя M-функцию MATLAB.
Определить является ли система системой «крамеровского» типа, делать проверку, сделать геометрическую иллюстрацию.
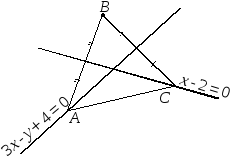
2. Даны координаты вершин треугольника АВС. Найти уравнение стороны ВС, а также уравнения медианы, высоты и биссектрисы, выходящих из вершины А. Все уравнения прямых дать в канонической и нормированной форме. Изобразить все прямые с использованием МАТЛАБ.
3. Даны канонические уравнения двух прямых в пространстве. Установить: скрещиваются, пересекаются или параллельны эти прямые. Если прямые пересекаются или параллельны, написать уравнение содержащей их плоскости. Если прямые скрещиваются, написать уравнение плоскости, содержащей первую прямую и параллельной второй прямой. Изобразить все используемые в задании объекты (прямые, плоскость, нормаль к плоскости).
4.
Написать
каноническое, параметрическое и общее
уравнение прямой, проходящей через
точки
 и
и
5.
Дана прямая
 Составить
уравнение прямой
Составить
уравнение прямой проходящей
через точку
проходящей
через точку и параллельной
прямой
и параллельной
прямой а также прямой
а также прямой проходящей
через точку
проходящей
через точку и перпендикулярной
прямой
и перпендикулярной
прямой
6.
Найти угол между прямыми
 и
и
7.Составить
уравнение прямой, симметричной прямой
 относительно:
относительно:
а)
начала координат; б) оси абсцисс; в)
точки


8.
Спроектировать
току
 на прямую
на прямую
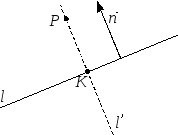
.
9.
Составить уравнение высоты
 медианы
медианы и биссектрисы
и биссектрисы треугольника
треугольника если
если



10.
Даны уравнения двух сторон параллелограмма:

 и координаты
его центра:
и координаты
его центра: Составить
уравнения двух других сторон и уравнения
диагоналей.
Составить
уравнения двух других сторон и уравнения
диагоналей.

11.
Даны координаты одной из вершин
треугольника:
 и уравнения
двух его медиан:
и уравнения
двух его медиан:
 Найти координаты
двух других вершин треугольника.
Найти координаты
двух других вершин треугольника.
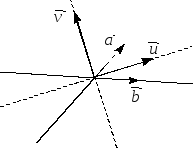
Указание.
Если
 и
и – векторы, то
вектор
– векторы, то
вектор – вектор,
направленный по биссектрисе угла,
образованного векторами
– вектор,
направленный по биссектрисе угла,
образованного векторами и
и а вектор
а вектор – по биссектрисе
смежного угла
– по биссектрисе
смежного угла
Если
 то
то а
а
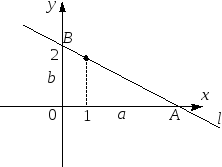
12.
Через точку
 провести
прямую, пересекающую положительные
части осей координат и образующую с
осями координат треугольник наименьшей
площади.
провести
прямую, пересекающую положительные
части осей координат и образующую с
осями координат треугольник наименьшей
площади.
13.
Найти все векторы, перпендикулярные
векторам
 и
и
14.
Вычислить
площадь треугольника с вершинами

 и
и
15.
Доказать
 . Изобразить
. Изобразить ,
, ,
, ,
, .
.
16.
Площадь параллелограмма, построенного
на векторах
 и
и равна
равна Найти площадь
параллелограмма, построенного на
векторах
Найти площадь
параллелограмма, построенного на
векторах и
и
17.
Найти
координаты единичного вектора
 перпендикулярного
векторам
перпендикулярного
векторам и
и
18.
Площадь треугольника
 равна
равна На сторонах
На сторонах

 соответственно
взяты точки
соответственно
взяты точки

 такие, что
такие, что

 Найти площадь
треугольника
Найти площадь
треугольника
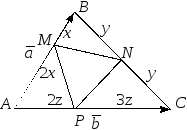
Рис.1.
19.
Пусть
 – некомпланарные
векторы. Найти значение
– некомпланарные
векторы. Найти значение при котором
следующие векторы компланарны:
при котором
следующие векторы компланарны:


20.
Даны точки
 и
и Составить
уравнение плоскости, проходящей через
точку
Составить
уравнение плоскости, проходящей через
точку перпендикулярно
отрезку
перпендикулярно
отрезку
21.
Составить
уравнение плоскости, проходящей через
точки

 и
и
22.
Найти угол
между плоскостями
 и
и
23.
Через точку
 провести
плоскость, параллельную плоскости
провести
плоскость, параллельную плоскости
24.
Составить уравнение плоскости,
симметричной плоскости

 относительно
точки
относительно
точки

25.
Составить
уравнение плоскости, симметричной
плоскости
 относительно
оси ординат.
относительно
оси ординат.
26.
Составить уравнение прямой
 параллельной
прямой
параллельной
прямой
 и проходящей
через точку
и проходящей
через точку
27.
Составить уравнение прямой, симметричной
прямой

 относительно
точки
относительно
точки

28.
Спроектировать точку
 на прямую
на прямую

29.
Найти точку,
симметричную точке
 относительно
плоскости
относительно
плоскости
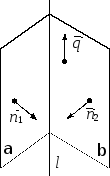
30.
Прямая
 задана как
пересечение плоскостей
задана как
пересечение плоскостей и
и Написать
каноническое уравнение этой прямой.
Написать
каноническое уравнение этой прямой.
31.
Составить уравнение высоты
 треугольника
треугольника если
если



32.
Определить, при каком
 прямые
прямые и
и пересекаются,
и для найденного значения
пересекаются,
и для найденного значения составить
уравнение плоскости, проходящей через
эти прямые.
составить
уравнение плоскости, проходящей через
эти прямые.

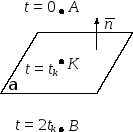
33.
В кубе
 точка
точка – середина
ребра
– середина
ребра Найти угол
между прямой
Найти угол
между прямой и плоскостью
и плоскостью

34.
Вычислить угол между прямой
 и плоскостью
и плоскостью
35.
Составить уравнение плоскости, проходящей
через точку
 параллельно
плоскости
параллельно
плоскости
36.
Составить уравнение плоскости, проходящей
через точки

 и параллельной
прямой
и параллельной
прямой
37.
Составить уравнение плоскости, проходящей
через ось ординат и точку

38.
Составить уравнение геометрического
места точек, равноудалённых от точек
 и
и
39.
Составить уравнение прямой, проходящей
через точку
 параллельно
прямой
параллельно
прямой
40.
Через точку
 провести
прямую, перпендикулярную плоскости
провести
прямую, перпендикулярную плоскости
41.
Через прямую
 провести
плоскость, параллельную прямой
провести
плоскость, параллельную прямой
42.
Через точку
 провести
плоскость, перпендикулярную плоскостям
провести
плоскость, перпендикулярную плоскостям и
и
43.
Составить уравнение плоскости,
симметричной плоскости
 а) относительно
начала координат,
б) относительно оси
а) относительно
начала координат,
б) относительно оси в) относительно
плоскости
в) относительно
плоскости г) относительно
плоскости
г) относительно
плоскости д) относительно
точки
д) относительно
точки
44.
Составить уравнение прямой, симметричной
прямой
 а) относительно
начала координат, б) относительно оси
а) относительно
начала координат, б) относительно оси в) относительно
плоскости
в) относительно
плоскости г) относительно
плоскости
г) относительно
плоскости д) относительно
точки
д) относительно
точки
45.
Найти точку пересечения плоскости
 и прямой,
проходящей через точки
и прямой,
проходящей через точки и
и
46.
При каких
 прямая
прямая а) параллельна
плоскости
а) параллельна
плоскости б) перпендикулярна
этой плоскости?
б) перпендикулярна
этой плоскости?
47.
При каких
 прямые
прямые и
и – скрещивающиеся?
– скрещивающиеся?
