Упражнение 13. Система двух однородных уравнений с тремя неизвестными

Придумать однородную систему вида (11) с единственным решением. Изобразить плоскости, прямую, нормальные векторы плоскостей и направляющий вектор прямой.

2. Система трех уравнений первой степени с тремя неизвестными

Рассмотрим систему уравнений с тремя неизвестными x,y,z.

(12)

Коэффициенты и свободные членысчитаются заданными.

Введем обозначения

,,,(13)

Определитель d, составленный из коэффициентов при неизвестных системы (11), называется определителем этой системы. Определительd_xполучается путем замены элементов первого столбца определителяdсвободными членами системы (11); определительd_yполучается из определителяdпри помощи замены свободными членами системы элементов его второго столбца, определительd_zполучается из определителяdпри помощи замены свободными членами системы элементов его третьего столбца.

Если d≠ 0, то система (11) называется системой крамеровского типа и имеет единственное решение см. рис. 16; оно определяется формулами Крамера

. (14)

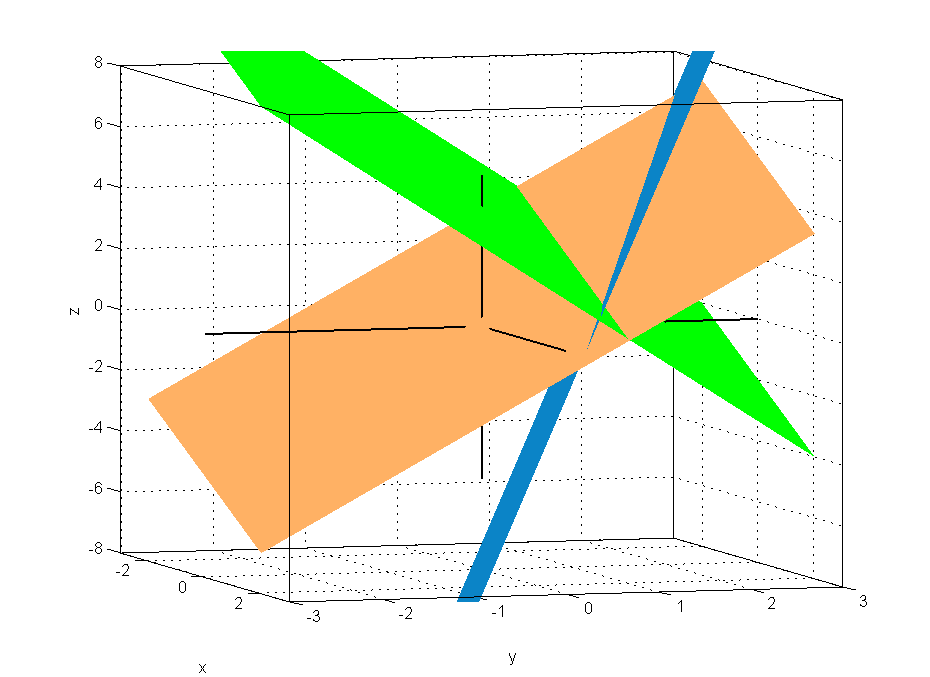
Рис. 16

Если d = 0, и при этом хотя бы один из определителей d_x,d_y,d_zотличен от нуля, то система (11) совсем не имеет решений (как говорят, уравнения этой системы несовместимы) см. Рис.17.

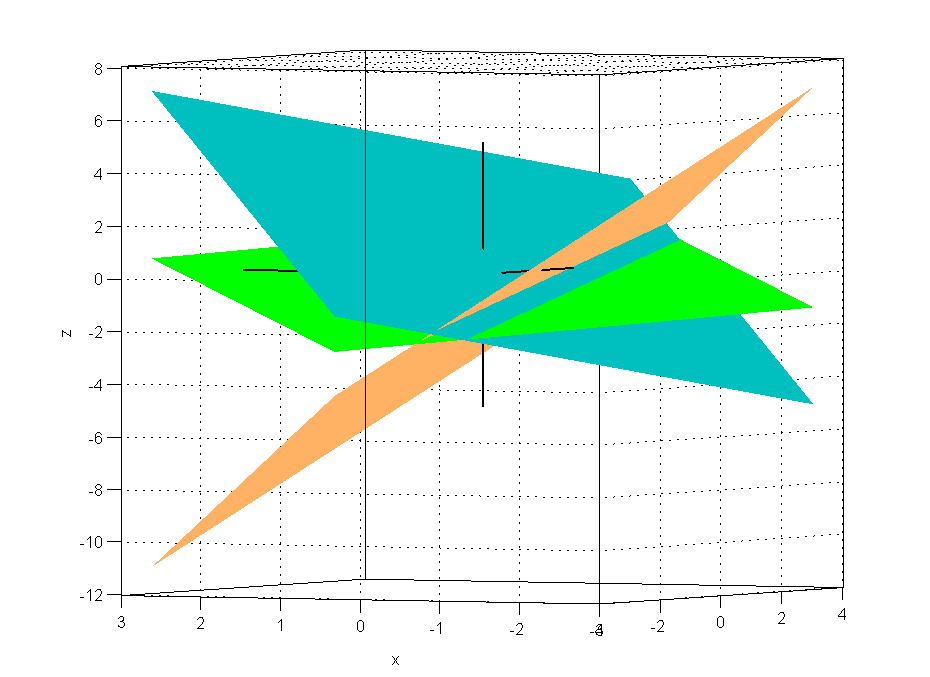
Рис. 17

Если же d = 0, но также d_x=d_y=d_z= 0, то система (11) также может совсем не иметь решений (рис.18);

Рис.18

но если система (11) при этих условия имеет хотя бы одно решение, то она имеет бесконечно много различных решений (рис.19).

Рис.19

Однородной системой трех уравнений первой степени с тремя неизвестными называется система вида

, (15)

то есть система уравнений, свободные члены которой равны нулю.

Однородная система всегда имеет нулевое решение: x= 0,y= 0,z = 0. Еслиd≠ 0, то это решение является единственным;

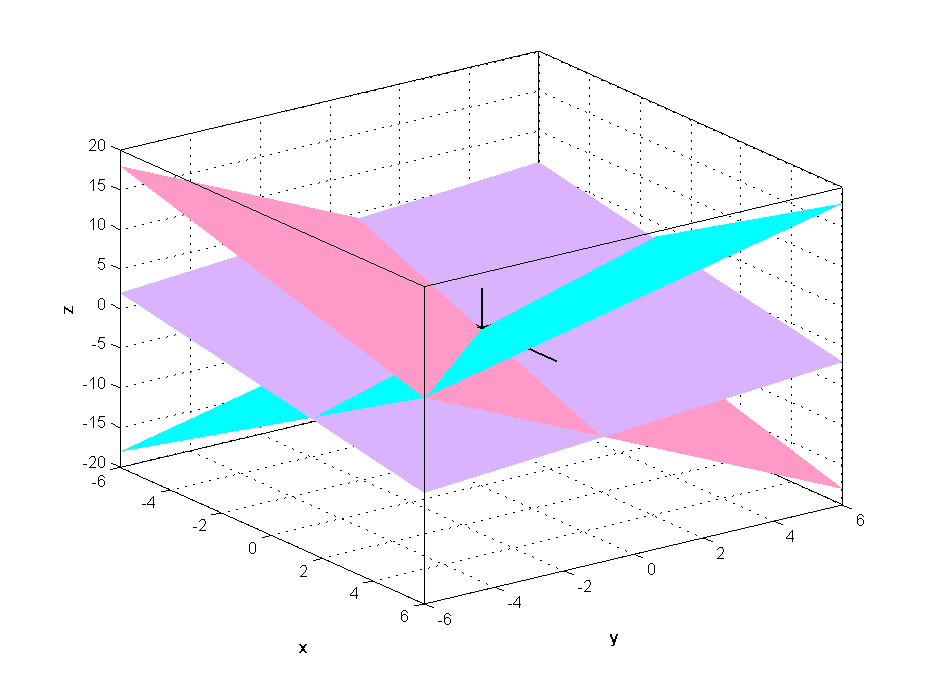
Рис. 20

если же d= 0, то система (15), кроме нулевого, имеет бесконечно много других решений.

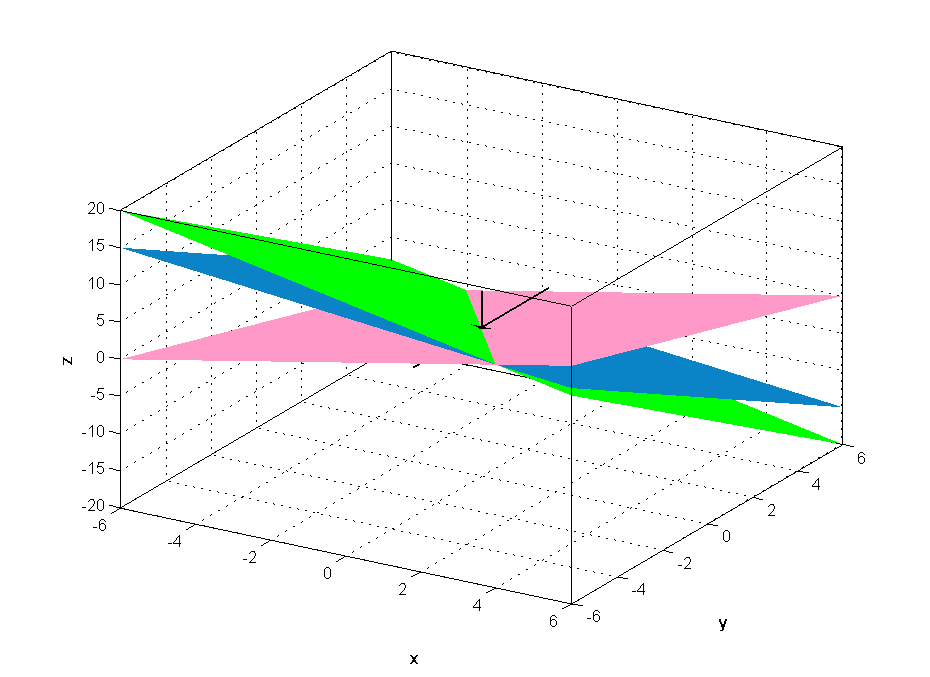
Рис.21.

Упражнение. 14. Система двух уравнений первой степени с двумя неизвестными.

Задача.Создать М-функцию, осуществляющую построение трех плоскостей по уравнениям, взятыми из системы вида (12), с необходимым количеством аргументов и использовать ее для иллюстрации решений для нижеследующих систем:

• изобразить уравнения систем в виде соответствующих плоскостей

• сделать предположения по взаиморасположению трех плоскостей в пространстве об отсутствии/наличии решений, количестве решений системы, уравнения которых записаны в системе

• вычислить для всех систем определители и сделать выводы о наличии/ отсутствии решений, о количестве решений системы, сравнить выводы с ранее сделанными предположениями.

• определить, которая из систем является системой крамеровского типа, решить ее по формулам Крамера; найти решения для других систем.

1) , 2), 3), 4),

5) 6)7), 8),

9. Задание для самостоятельной работы

1. Выполнить в тетради и в MATLABвсе упражнения данного практикума.

2. Ответить на контрольные вопросы (некоторые *темы* изучить самостоятельно*)

3. Уметь отвечать на вопросы по темам презентаций, даже если презентацию вы не готовите.

4. Подготовить краткую презентацию (5–7 минут) с применением графических средств MATLAB, и выступить с ней у доски. Презентация должна включать в себя вопросы к аудитории.

Темы для презентаций:

1) Система двух уравнений первой степени с двумя неизвестными как взаимное расположение двух прямых линий.

2) Неполные уравнения прямых на плоскости и в пространстве.

3) Неполные уравнения плоскостей в пространстве.

4) Физический смысл векторного произведения (найти, соответствующую информацию переработать и рассказать)