2. Общее уравнение прямой в пространстве.

Общее уравнение прямой в пространстве очень отличается от общего уравнения прямой на плоскости.

Прямую линию в пространстве можно задать как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений.

(8)

Сведем уравнение (8) к уравнению (6) или (7).

На рисунке мы видим две пересекающиеся плоскости по красной прямой линии, три синих перпендикуляра; два из которых – нормали к плоскостям, а третий – направляющий вектор прямой линии.

Рис. 15.

Каждое из уравнений определяет плоскость. В том случае, если заданные плоскости не параллельны (координаты нормальных векторов не пропорциональны), то система уравнений определяет прямую линию Lкак геометрическое место точек пространства, координаты которых удовлетворяют каждому из этих уравнений. Таким образом, прямаяLс направляющим векторомпринадлежит обеим плоскостям. Значит, нормальные векторы к плоскостям перпендикулярны направляющими вектору. Стало быть, векторможно найти при помощи векторного произведения:, а его координаты при помощи векторного произведения, записанного в координатной форме:

.

По любой точке , удовлетворяющей обоим уравнениям системы (8) и направляющему векторуможно составить каноническое или параметрическое уравнение прямой в пространстве.

Упражнение 12. Общее уравнение прямой в пространстве.

Найти угол Phi между плоскостями 3 x + 4 y + 6 z – 12 = 0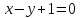и 6 x + 3 y + 4 z – 12 = 0. (Угол между плоскостями - это угол между их нормальными векторами) Построить линию, являющуюся пересечением двух плоскостей, заданных общими уравнениями (построить обе плоскости). Построить нормальные векторы к плоскостям из точкиМ₀принадлежащей обеим плоскостям. Найти направляющий вектор прямой, построить его из точкиМ₀. Составить каноническое уравнение прямой и вывести его в названии к графику.

8. Система двух и трех уравнений первой степени с тремя неизвестными и их геометрическая интерпретация.

   1. Система двух однородных уравнений с тремя неизвестными

Рассмотрим систему двух однородных уравнений с тремя неизвестными x, y, z.

(9)

Однородные системы всегда имеют решения: единственное (тривиальное) или бесконечное число решений.

Введем обозначения

;;. (10)

Если хотя бы один из определителей не равен нулю, то все решения системы будут определяться по формулам

x = q₁t,y = q₂t,z = q₃t, (11)

где t– произвольное число. Каждое отдельное решение получается при каком-либо определенном значенииt.

Если все три определителя системы равны нулю, а коэффициенты уравнений системы пропорциональны. В этом случае одно из уравнений системы есть следствие другого, и система сводится к одному уравнению. Такая система имеет бесконечное множество решений; чтобы получить какое-нибудь из них, следует двум неизвестным придать произвольные численные значения, а третье найти из уравнения.

Геометрическая интерпретация.

Каждое из уравнений системы (9) представляет собой общее уравнение плоскости, проходящей через начало координат. Две плоскости, проходящие через начало координат могут либо пересекаться по общей прямой, либо совпадать. Это соответствует тому, что однородные системы всегда имею решение.

Формулы (11) представляют собой параметрическое задание прямой, проходящей через начало координат, с направляющим вектором .

По заданной точке O(0,0,0) и направляющему векторуможно составить каноническое или параметрическое уравнение прямой в пространстве. Прямая будет единственна, а значит решение системы (8) в этом случае является тривиальным (единственным).

Если все три определителя системы равны нулю, а коэффициенты уравнений системы пропорциональны. В этом случае одно из уравнений системы есть следствие другого, и система сводится к одному уравнению. То есть множество решений системы лежат в плоскости, задаваемой уравнением системы. Мы можем выразить , и, придавая любые значенияxиy, находить значенияz. Каждый такой набор (x,y,z) - является решением системы (11),геометрически представляет собой бесконечное множество прямых линий, принадлежащих одной плоскости.