Упражнение 11. Уравнение плоскости в отрезках.

Составить уравнение плоскости в отрезках, отсекающей на осях координат OxиOyотрезки, соответственно равные 5 и 7, и проходящей через точкуM₀(1,1,2).

Построить плоскость. Построить нормальный вектор (с помощью line)

В координатном пространстве построить черным цветом толщиной 1.5 пункта оси координат, на которых в местах пересечений с плоскостью вывести круговые маркеры синего цветаи обозначить координаты точек пересечения плоскости с осями координат. Вывести обозначение осей и заголовок координатного пространства, в котором написать уравнение плоскости в отрезках.

7. Прямая в пространстве.

   1. Параметрическое и каноническое уравнение прямой в пространстве.

Начнем с параметрического задания уравнения прямой в пространстве. В векторном виде эта задача не отличается от плоской. Пусть теперь в пространстве задана прямая, проходящая через точку в направлении вектора.

Рис. 11

Рассмотрим вектор , где- любая точка прямойL. Введем параметр t – любое вещественное число, см. рис.11.

Условие коллинеарности прямой и направляющего вектора с помощью параметра t можно записать в виде векторного уравнения: .

Геометрический смысл параметра прямой t тот же:

• модуль числа означает, сколько векторов“укладывается” на векторе,

• знак обозначает расположение точки на прямойL относительно :

при точканаходится с той стороны, куда направлен векторпри– в противоположной стороне, см. рис. 12.

Рис. 12

Параметрическое уравнение прямой в векторной форме однозначно определяет прямую Lв пространстве и не зависит от системы координат.

Введем декартовую прямоугольную систему координат OXYZ, координаты точки, координаты направляющего вектораи координаты произвольной точки прямой.

Как было сказано выше, условие коллинеарности направляющего вектора и прямой - условие пропорциональности соответствующих координат векторов и . Вместе с параметромtиз векторного уравнения получаем соотношение:

(5)

Рис. 13

Из уравнения (5) получаем три соотношения:

(6)

Уравнение (6) называется параметрическим уравнением прямой L, проходящей через точкупараллельно направлению вектора

Уравнение (5) дает также каноническое уравнение прямой:

(7)

Вещественные числа k,l,mне должны одновременно равняться нулю.

Пример.3. Построение прямой в пространстве, заданной параметрически.

Изобразить прямую, заданную параметрическим уравнением .

Решение:

Входящими параметрами в систему MATLABявляются

1. параметр прямой t;

2. точка через которую проходит прямая и координаты которой следуют из параметрического уравнения прямой при t = 0:

3. координаты направляющего вектора

Создадим скрипт:

% включим режим добавления графиков

hold on

% для построения прямой достаточно двух точек

% параметр прямой t зададим вектором-строкой,

% состоящим из двух элементов – 2 и 2,

% соответствующих начальной (t=-2) и конечной (t=2) точкам

% изображаемой прямой

t=[-2,2];

% зададим числовые координаты точки M0

% и направляющего вектора q

x0=1; y0=-2; z0=-1; q1=5; q2=2; q3=-1;

% координаты точки M0 и направляющего вектора q

% зададим в общем виде вектор-столбцами!

% задание массивов M0 и q вектор-столбцами необходимо для дальнейшего

M0=[x0;y0;z0]; q=[q1;q2;q3];

% следующая команда создаст матрицу 3х2, в которой

%первый столбец - координаты начальной (t=-2) точки прямой

%второй столбец - координаты конечной (t=2) точки прямой

xyz=M0*ones(size(t))+q*t;

% size(t) - выдает размерность массива t: 1 2

% первое число количество строк массива, второе - количество столбцов

% ones(size(t)) - создает единичную матрицу,

% то есть матрицу, состоящую из единиц,

% той же размерности, что и массив t

% M0*ones(size(t)) перемножает матрицу M0 размерности 3х1

% и единичную матрицу размерности 1х2

% в результате получаем матрицу размерности 3х2

% в первом и втором столбце которой - координаты точки M0

% q*t также перемножает вектор-столбец q 3х1 и вектор-строку t 1х2

% дает матрицу 3х2, первый столбец которой суть вектор "-2*q"

% второй столбец суть вектор "2*q"

% сумма двух матриц M0*ones(size(t))+q*t дает также матрицу 3х2,

% первый столбец которой координаты начальной (t=-2) точки прямой,

% получаемые в результате "приложения" вектора "-2q" к точке M0

% второй столбец - результат "приложения" 2q к точке M0

%второй столбец - координаты конечной (t=2) точки прямой

% следующая команда строит саму прямую по двум узловым точкам

% отметим их маркерами «*»

L=plot3(xyz(1,:), xyz(2,:), xyz(3,:),'*-r','LineWidth',2,...

'MarkerEdgeColor','r',...

'MarkerSize',8);

% команда xyz(1,:) считывает первую строку матрицы xyz

% создавая данные для диапазона абсцисс - две точки [x1, x2]

% команда xyz(2,:) считывает вторую строку матрицы xyz

% создавая данные для диапазона ординат - две точки [y1, y2]

% команда xyz(3,:) считывает третью строку матрицы xyz

% создавая данные для диапазона аппликат - две точки [z1, z2]

% оформление графика

% строим оси координат

line([xyz(1);xyz(4)], [0;0],[0;0],'LineWidth',1.5, 'Color', 'black' )

line([0;0],[xyz(2);xyz(5)],[0;0], 'LineWidth',1.5, 'Color', 'black' )

line([0;0],[0;0],[xyz(3);xyz(6)], 'LineWidth',1.5, 'Color', 'black' )

% включим отображение координатной сетки

grid on

% одинаковый масштаб по осям

axis equal

% обозначение осей и ввод заголовка

xlabel('x'), ylabel('y'), zlabel('z')

title('прямая x=1+5t, y=-2+2t, z=-1-t')

view(64,4)

% изобразим направляющий вектор из начала координат

plot3([0,q1], [0,q2], [0,q3],'-b','LineWidth',2);

plot3(q1,q2,q3,'>b','LineWidth',2,...

'MarkerEdgeColor','b',...

'MarkerSize',8)

% пометим точку M0

plot3(x0,y0,z0,'o','LineWidth',2,...

'MarkerEdgeColor','k',...

'MarkerSize',8)

text (x0-0.5,y0-0.5,z0-1.5,'M_0')

% изобразим направляющий вектор из точки М0

t=[0,1];

xyz=M0*ones(size(t))+q*t;

plot3(xyz(1,:), xyz(2,:), xyz(3,:),'-b','LineWidth',4);

plot3(xyz(4), xyz(5), xyz(6),'>b','LineWidth',2,...

'MarkerEdgeColor','b',...

'MarkerSize',8)

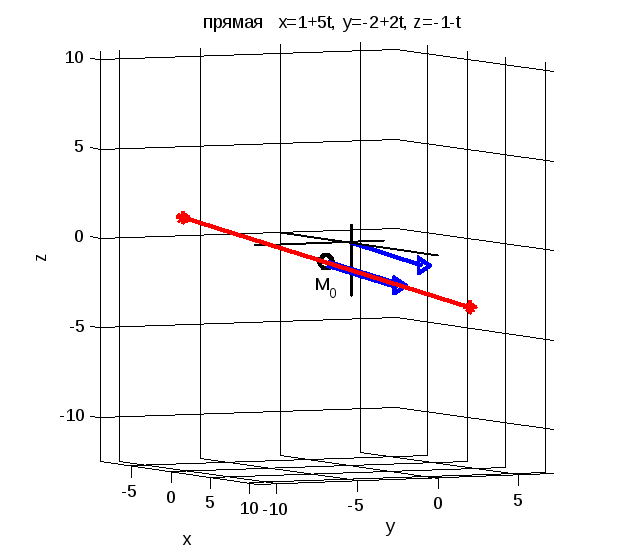
Рис. 14.