Пример 2. Построение плоскость по общему уравнению с помощью функций mesh(),surf(), surfl().
Построить плоскость, заданную общим уравнением 3 x+ 4y+ 6z– 12 = 0. Вывести обозначения осей заголовок координатного пространства. Изобразить также нормальный вектор к этой прямой, выходящим из начала координат.
В примере 2 мы построим плоскость по общему уравнению с помощью функций mesh(), surf(), surfl(), см. рисунки 6, 7, 8,9, а также с помощью функции surface(), рис. 10.
%Общее уравнение плоскости 3x + 4y + 6z - 12 = 0
% Вводим исходные параметры
A = 3; B = 4; C = 6; D = -12;
% Задаем диапазоны изменения переменных x и y
x = -4:1:4; y = -3:1:3;
% создаем матрицы, содержащие координаты узлов пространственной сетки
[X,Y]=meshgrid(x,y);
% выражаем Z
Z = (-A*X-B*Y-D)/C;
figure
% оформление графика
% включим отображение координатной сетки и режим добавления графиков
grid on, hold on
% одинаковый масштаб по осям
axis equal
% обозначение осей и ввод заголовка
xlabel('x'), ylabel('y'), zlabel('z')
title('3x + 4y - 4z - 12 = 0, mesh')
% строим оси координат
line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',1.5, 'Color', 'black' )
view(64,6)
% строим поверхность и нормаль
mesh(X,Y,Z)
% mesh выводит в координатное пространство поверхность в виде сетки
line([0;A],[0;B],[0;C], 'LineWidth',2 ) % строим нормальный вектор из начала координат
figure
% оформление графика
% включим отображение координатной сетки и режим добавления графиков
grid on, hold on
% одинаковый масштаб по осям
axis equal
% обозначение осей и ввод заголовка
xlabel('x'), ylabel('y'), zlabel('z')
title('3x + 4y - 4z - 12 = 0, surf ')
% строим оси координат
line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',1.5, 'Color', 'black' )
view(64,6)
% строим поверхность и нормаль
surf(X,Y,Z)
line([0;A],[0;B],[0;C], 'LineWidth',2 ) % строим нормальный вектор из начала координат
figure
% оформление графика
% включим отображение координатной сетки и режим добавления графиков
grid on, hold on
% одинаковый масштаб по осям
axis equal
% обозначение осей и ввод заголовка
xlabel('x'), ylabel('y'), zlabel('z')
title('3x + 4y - 4z - 12 = 0, surf + shading interp')
% строим оси координат
line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',1.5, 'Color', 'black' )
view(64,6)
% строим поверхность и нормаль
surf(X,Y,Z)
shading interp %убирает сетку на плоскости и делает плавный переход цвета
line([0;A],[0;B],[0;C], 'LineWidth',2 ) % строим нормальный вектор из начала координат
figure
% оформление графика
% включим отображение координатной сетки и режим добавления графиков
grid on, hold on
% одинаковый масштаб по осям
axis equal
% обозначение осей и ввод заголовка
xlabel('x'), ylabel('y'), zlabel('z')
title('3x + 4y - 4z - 12 = 0, surfl')
% строим оси координат
line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',1.5, 'Color', 'black' )
view(64,6)
% строим поверхность и нормаль
surfl(X,Y,Z)
line([0;A],[0;B],[0;C], 'LineWidth',2 ) % строим нормальный вектор из начала координат
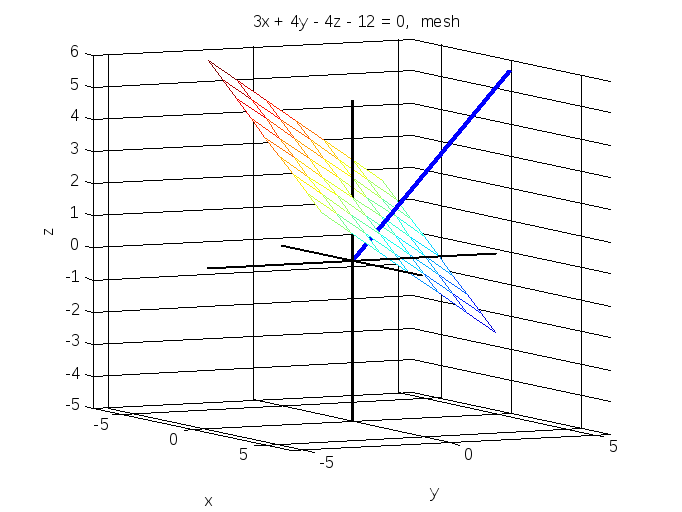
mesh выводит в координатное пространство поверхность в виде сетки
Рис.6.
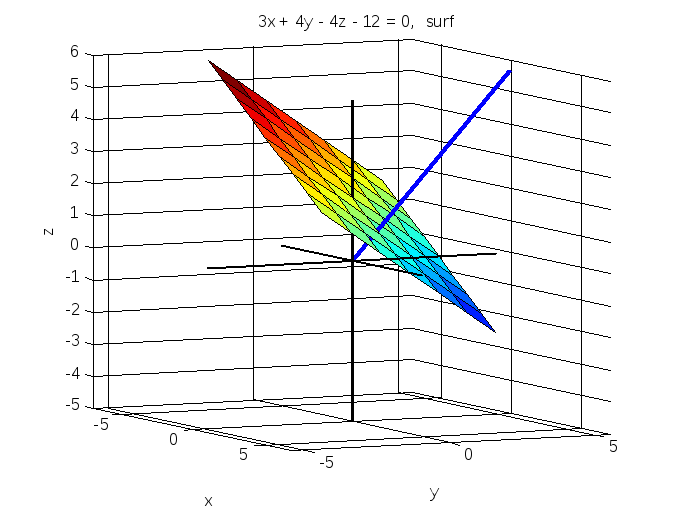
Рис. 7.
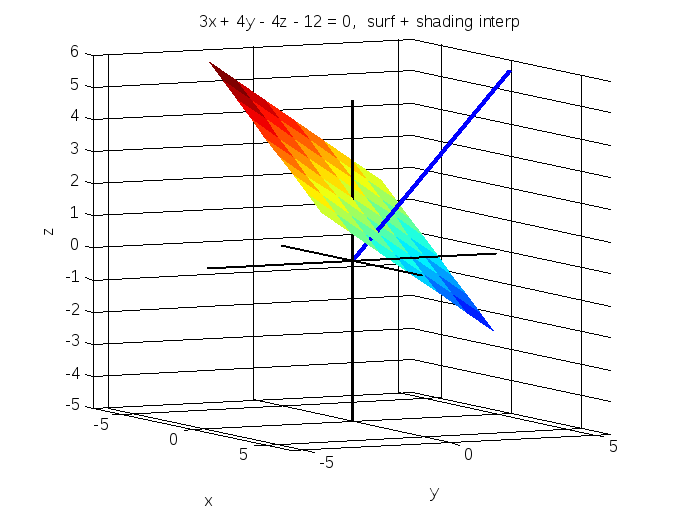
Рис.8.
Рис.9.
Функция surface(X,Y,Z) также позволяет строить поверхности
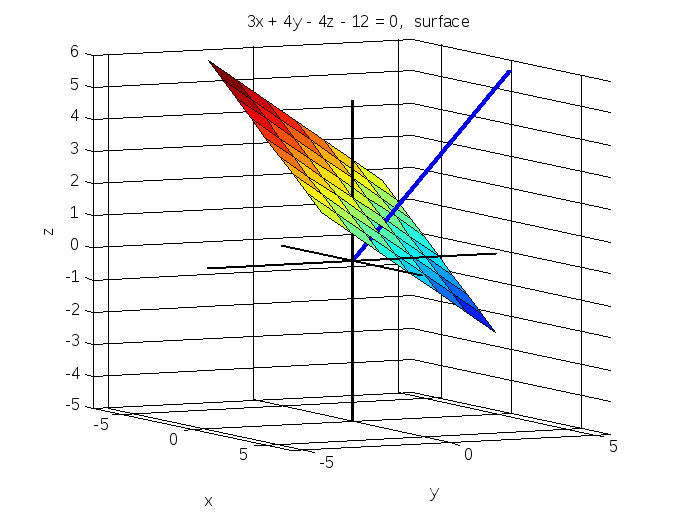
Рис. 10.