4. Метод простой итерации для решения систем.

Рассмотрим итерационный (численный) метод решения систем. Таких методов существует множество, мы рассмотрим один (не самый лчший)

Будем решать системуметодом простой итерации.

Преобразуем систему, разделив каждую строчку на диагональный элемент: матрица системы и столбец свободных членов изменятся. ( Все значения главной диагонали – ведущие элементы, в методе Гаусса мы предполагали, что они не равны нулю.)

Запишем новую систему в виде,- единичная матрица.E=eye(n),n– размерность системы.

Итак

. Для сходимости итерационного процесса должно выполняться

одно из условий для матрицы :

а) в матлабе этоnorm(C,1) – первая норма матрицы – максимальное число, получающееся после суммирования абсолютных значений элементов матрицы по столбцам

б) в матлабе этоnorm(C,inf) – бесконечная норма матрицы - максимальное число, получающееся после суммирования абсолютных значений элементов матрицы по строкам

в) - в матлабе этоnorm(C, 'fro') -Евклидова или Фробениусова норма – сумма квадратов элементов матрицы.

Вместо трех условий достаточно проверить то, что каждое собственное значение матрицы Cпо абсолютному значению меньше 1:

Собственные значения можно найти с помощью команды[D]=eig( C ).

Они будут стоять на главной диагонали матрицы D.

Упражнение 12.

Записать систему уравнений в виде .

Проверить выполнение (а, б, в и ) условий для матрицы.

Создать M-функцию для решения методом простой итерации системы уравнений, взяв в качестве начального приближения решения- столбец свободных членов. Выходные параметры: приближённое решение, количество итераций и длины невязки. Решить систему уравнений с точностью 0,001, оценив предварительно (вручную) необходимое число шагов.

В процессе итераций

создайте

• матрицуприближенных решенийV=[x1 x2 x3… xk],

где xk-решение получаемое наk-ом шаге,

матрица Vформируется:V=b, V=[V x] ,

постройте

• график приближенных решений в зависимости от номера итерации командой plot(V'), добавьтеpauseдля задержки вывода на экран, выводите при этомVи номер шагаk-1.

• график зависимости длины вектора невязки от итерации plot(0:k,d1, '*') матрицаd1 формируетсяd1=[d1norm(b-A*x)], выводите при этомd1.

Обратите внимание на то, что метод простой итерации для некоторых систем сходятся, а достаточные условия этой системы не выполняются.

Проверить решение подстановкой.

Ответьте на вопрос: всегда ли годится вектор свободных значений системы для первого приближения?

Файл в помощь (его придется существенно дополнить)

% рассмотрим систему

A=[7 2 3;5 -3 2;10 -11 5];

b=[15;15;36];

%%%% сам метод

% метод простой итерации

% первый м-файл

% за начальный вектор приближений берем правый столбец свободных членов x=b;.

x=b;

V=b;

k=1; % счетчик числа итераций

xx=zeros(3,1); % формируем вектор решений

% zeros(3,1); формирует вектор-столбец – 3 строки на 1 столбец,

% состоящий их нулей

AA=[A b]; % расширенная матрица системы

% размера n строк на n+1 столбцов

% формируем цикл по числу уравнений (строк)

for i=1:3 AA(i,:)=AA(i,:)/AA(i,i);

% на первом шаге 1-ую строку делим на 1-ый диагональный элемент

% на втором шаге вторую строчку

% делим на второй диагональный элемент

% итд.

end

% формируем цикл для поиска и построения решений

for k=1:180;

xx(1)=-AA(1,2)*x(2)-AA(1,3)*x(3)+AA(1,4);

xx(2)=-AA(2,1)*x(1)-AA(2,3)*x(3)+AA(2,4);

xx(3)=-AA(3,1)*x(1)-AA(3,2)*x(2)+AA(3,4);

x=xx;

k=k+1;

V=[V x];

plot(V')

V

k1= k-1

pause

end

С командой pause будем работать так:

при первом появлении графика закрепляем его на рабочем столе, так, чтобы следить за процессом и на графике, и в командном окне.

При активном командном окне нажимаем любую клавишу для продолжения работы программы до тех пор, пока не поймем, что требуемая точность 0,001 достигнута. Находим, на каком шаге была достигнута точность. То есть, начиная с какого шага, ни одна компонента вектора решений не меняется в третьем знаке после запятой.

Остановить процесс выполнения программы можно с помощью нажатия клавиш «ctrl+c» при активном командном окне

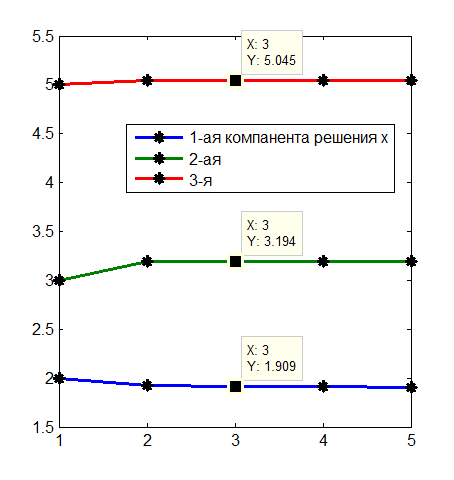
Например, для некоторой системы график будет меняться так

V =

2.0000 1.9200

3.0000 3.1900

5.0000 5.0400

k1 = 1 % первый шаг

Вектор b=(2 3 5) – начальный вектор приближений, - первый столбец и первый набор точек на графике, второй столбец матрицыV– решение, полученное после первой итерации.

V =

2.0000 1.9200 1.9094

3.0000 3.1900 3.1944

5.0000 5.0400 5.0446

ans =

2

V =

2.0000 1.9200 1.9094 1.9092 1.9092

3.0000 3.1900 3.1944 3.1949 3.1950

5.0000 5.0400 5.0446 5.0448 5.0448

k1 = 4

По рисунку и по матрице Vвидно, что требуемую точность решение достигает на втором шаге.

% сформируйте второй цикл while_end if_end для автоматического поиска k1 по заданной точности 0,001.

% второй м-файл – формируем цикл

k=1 % сбрасываем счетчик, к1 теперь известно

d1= norm(b-A*b) % длина вектора невязки

for k=1:k1; ……

xx(1)=-AA(1,2)*x(2)-AA(1,3)*x(3)+AA(1,4);

xx(2)=-AA(2,1)*x(1)-AA(2,3)*x(3)+AA(2,4);

xx(3)=-AA(3,1)*x(1)-AA(3,2)*x(2)+AA(3,4);

x=xx;

k=k+1;

V=[V x];

plot(V')

d1=norm(b-A*b)

d1=[d1 norm(b-A*x)]

plot(0:k,d1, '*')

pause(0.2) % 0.2 – секунды автоматической задержки

Замечание. Мы рассматривали совместную систему с заведомо единственным решением. Но существуют и другие системы, например, несовместные системы с числом m уравнений большим числа n неизвестных. Такие системы при формальном подходе могут не иметь решений. Но такие системы берутся из жизни и должны иметь путь к решению, и пути такие есть, например, метод наименьших квадратов и др методы. Но и такие системы часто приводят к плохо обусловленным матрицам. Есть способ бороться плохо обусловленными системами. Об этом читайте в Л.5 и Л.1, и в другой различной литературе по численным методам.