Лабораторная работа №5Лабораторная работа №5 Ярослав Ермилов (МП-14)

Лабораторная работа №5

Предел последовательности

Работу выполнил: Ермилов Ярослав (МП-14)

Упражнение 1.

Создать символьное число вычислить значения при . вернуть значение системной константы, снова вычислить . Проверить равенство полученных результатов с помощью логической операции. Объяснить результат.

>> pi = sym(pi);

pi = pi

>> k = 1:1:10;

>> u = cos((pi/2)*k)

u = [ 0, -1, 0, 1, 0, -1, 0, 1, 0, -1]

>> clear pi

v =

Columns 1 through 3

0.000000000000000 -1.000000000000000 -0.000000000000000

Columns 4 through 6

1.000000000000000 0.000000000000000 -1.000000000000000

Columns 7 through 9

-0.000000000000000 1.000000000000000 0.000000000000001

Column 10

-1.000000000000000

>> v == u

ans = 0 1 0 1 0 1 0 1 0 1

Упражнение 2.

Задать символьные переменные х и y. Задать z - массив . Проверить наличие символьных переменных. Сделать вывод.

>> syms x y;

>> z = [cos(x) sin(x); -sin(x) cos(x)];

z =

[ cos(x), sin(x)]

[ -sin(x), cos(x)]

>> whos

Name Size Bytes Class Attributes

x 1x1 112 sym

y 1x1 112 sym

z 2x2 112 sym

Упражнение 3.

Задать массив с элементами , и упростить его.

>> x = sym('x')

x = x

>> z=[(x^7+3*x^2-4)/(x-1) sqrt(x^2)/x]

z = [ (x^7+3*x^2-4)/(x-1), (x^2)^(1/2)/x]

>> simplify(z)

ans = [ x^6+x^5+x^4+x^3+x^2+4*x+4, csgn(x)]

Упражнение 4.

Разложить на множители:

a) ; б) ; в) 123456789 г) .

>> factor(x^4+4)

ans = (x^2 - 2*x + 2)*(x^2 + 2*x + 2)

>> factor(x^7+1)

ans = (x + 1)*(x^6 - x^5 + x^4 - x^3 + x^2 - x + 1)

>> factor(123456789)

ans = 3 3 3607 3803

>> factor(2*x^3+x^2*y-5*x*y^2+2*y^3)

ans = (x - y)*(2*x - y)*(x + 2*y)

Упражнение 5.

Решить неравенство, получить точный и приближённый ответ:

clf; axis equal; grid on; hold on;

x = -1:0.1:1.5;

y = x.^3+3*x-3;

plot(x,y, 'lineWidth', 2);

X_min = -0.5; X_max = 1.5;

Y_min = -0.5; Y_max = 1.5;

axis([X_min X_max Y_min Y_max]);

title('x.^3+3*x-3 > 0');

% создаём оси X,Y

quiver(X_min, 0, X_max-X_min, 0, 1, 'black', 'lineWidth', 2);

quiver(0, Y_min, 0, Y_max-Y_min, 1, 'black', 'lineWidth', 2);

Найдём точку пересечения с осью х

>> x = fzero(@(x)(x^3+3*x-3), 1)

x = 0.8177

Значит, решением неравенства является луч

Другой способ:

>> syms x

>> maple('solve','{x^3+3*x>3}',x)

ans = {1/2*(12+4*13^(1/2))^(1/3)-2/(12+4*13^(1/2))^(1/3) < x}

>> vpa(ans,5)

ans = {.81770 < x}

Упражнение 6.

Написать М-файл с параметрами осуществляющий следующие действия:

1. Задаёт массив n номеров от до

2. Строит график последовательности на указанном промежутке.

3. Строит прямые .

Для последовательностей : 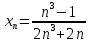; б) выполнить:

1. Найти .

2. Вычислить , . Результат оформить в виде таблицы

	а)	б)
	7	50
	22	500

3. С помощью созданного М-файла построить графическую иллюстрацию.

Указание. При задании формулы x(n) не забывайте, что n – это массив.

1.

>> syms n;

>> limit((n^3-1)/(2*n^3+2*n), inf);

ans = 1/2

>> limit((n^3+2*n)/(2*n^4+1), inf);

ans = 0

2.

>> maple('solve','{abs((n^3-1)/(2*n^3+2*n)-1/2)<0.01,n>0}',n);

ans = {7.463211680 < n}

>> maple('solve','{abs((n^3-1)/(2*n^3+2*n)-1/2)<0.001,n>0}',n)

ans = {22.82339470 < n}

>> maple('solve','{abs((n^3+2*n)/(2*n^4+1))<0.01,n>0}',n)

ans = {n < .4999937508e-2, 0. < n}, {50.03993219 < n}

>> maple('solve','{abs((n^3+2*n)/(2*n^4+1))<0.001,n>0}',n)

ans = {n < .4999999375e-3, 0. < n}, {500.00399993 < n}

3. Текст файла lab_5_u_5.m

function lab_5_u_5(xn, n0, a, epsilon)

n = n0-5 : 0.1 : n0+10;

clf; grid on; hold on

x = eval(xn);

plot(n,x,'b-');

N_min = n0-5; N_max = n0+10;

X_min = 0.35; X_max = 0.55;

axis([N_min N_max X_min X_max]);

line([N_min N_max],[a-epsilon a-epsilon],'Color','r');

line([N_min N_max],[a+epsilon a+epsilon],'Color','r');

xlim([N_min N_max]);

end

>> lab_5_u_5('(n.^3-1)./(2.*n.^3+2.*n)', 7, 1/2, 0.01)

>> lab_5_u_5('(n.^3-1)./(2.*n.^3+2.*n)', 22, 1/2, 0.001)

>> lab_5_u_5('(n.^3+2.*n)./(2.*n.^4+1)', 50, 0, 0.01)

>> lab_5_u_5('(n.^3+2.*n)./(2.*n.^4+1)', 500, 0, 0.001)

Упражнение С1

Решить неравенство , получить точный и приближённый ответ. Объяснить результат.

>> syms x

>> maple('solve','{(x^3 -3*x+1)>0}',x)

ans

{-1/4*(-4+4*i*3^(1/2))^(1/3)-1/(-4+4*i*3^(1/2))^(1/3)+1/2*i*3^(1/2)*(1/2*(-4+4*i*3^(1/2))^(1/3)-2/(-4+4*i*3^(1/2))^(1/3)) < x, x < -1/4*(-4+4*i*3^(1/2))^(1/3)-1/(-4+4*i*3^(1/2))^(1/3)-1/2*i*3^(1/2)*(1/2*(-4+4*i*3^(1/2))^(1/3)-2/(-4+4*i*3^(1/2))^(1/3))}, {1/2*(-4+4*i*3^(1/2))^(1/3)+2/(-4+4*i*3^(1/2))^(1/3) < x}

>> x = fzero(@(x)(x.^3+3*x-3), 1)

x = 0.8177

>> x=[-10:1:10]

>> xlabel('x')

>> ylabel('y')

>> plot(x.^3 -3*x+1)

Упражнение С2

Для последовательностей :

а) ; б) ;

в) .

выполнить:

1. Найти .

>> syms n

>> limit( (2*n^5 + 2*n^4 + 3)/(n^5 - 5*n - 1000), inf )

ans = 2

>> limit( sqrt(2*n^5+3)/sqrt(n^5-5), inf )

ans = 2^(1/2)

>> limit( (n^3+n^2)^(1/3) - (n^3-n^3)^(1/3), inf )

ans = Inf

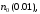
2. Вычислить . Результат оформить в виде таблицы

>> syms n

>> maple('solve','{abs((2*n^5 + 2*n^4 + 3)/(n^5 - 5*n - 1000)-2)<0.01,n>0}')

ans = {200.00025143639352590051410231757 < n}

>> maple('solve','{abs((2*n^5 + 2*n^4 + 3)/(n^5 - 5*n - 1000)-2)<0.001,n>0}')

ans = {2000.0000013758749970742878150528 < n}

>> maple('solve','{abs( sqrt(2*n^5+3)/sqrt(n^5-5) - sqrt(2) )<0.01,n>0}')

ans = {3.4128423170561715893297846786104 < n}

>> maple('solve','{abs( sqrt(2*n^5+3)/sqrt(n^5-5) - sqrt(2) )<0.001,n>0}')

ans = {5.4018614376064026873350098540908 < n}

	а)	б)
	7	50
	22	500

3. С помощью созданного М-файла построить графическую иллюстрацию.

Указание. При задании формулы x(n) не забывайте, что n – это массив.

>> xn='(2.*n.^5 + 2.*n.^4 + 3)./(n.^5 - 5.*n - 1000)'; a=2; epsilon=0.01; n0=200;

>> graph

>> xn='(2.*n.^5 + 2.*n.^4 + 3)./(n.^5 - 5.*n - 1000)'; a=2; epsilon=0.001; n0=2000;

>> graph

>> xn='sqrt(2.*n.^5+3)./sqrt(n.^5-5)'; a=sqrt(2); epsilon=0.01; n0=3;

>> graph

>> xn='sqrt(2.*n.^5+3)./sqrt(n.^5-5)'; a=sqrt(2); epsilon=0.001; n0=5;

>> graph

-12- 21.07.2019