Пример 3. Построение ортонормированного базиса

Построить ортонормированный базис подпространства пространства натянутого на систему векторови

Решение.Нам требуется построить ортонормированный базис евклидова пространствакоторое является линейной оболочкой векторовПрименим к этим векторам процесс ортогонализации.

Вначале возьмём Векторбудем искать в видеИз условия перпендикулярностиполучаем:Следовательно,Далее, следующий базисный вектор будем искать в видеИз условийиполучаем:и

Отсюда Таким образом, ортогональный базис пространстватаков:Ортонормированный базис получится, если мы разделим каждый вектор на его длину:

Пример.4 Дополнение системы векторов до ортогонального базиса.

Убедиться в том, что векторы ортогональны, и дополнить систему этих векторов до ортогонального базиса.

Решение.Проверим ортогональность. Имеем:Следовательно,Таким образом, мы можем положитьДругие векторыортогонального базиса удовлетворяют условиямиПустьУсловиедаёт систему

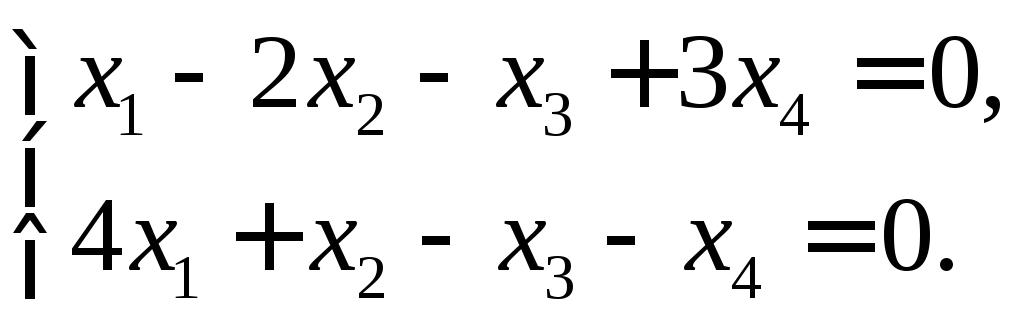
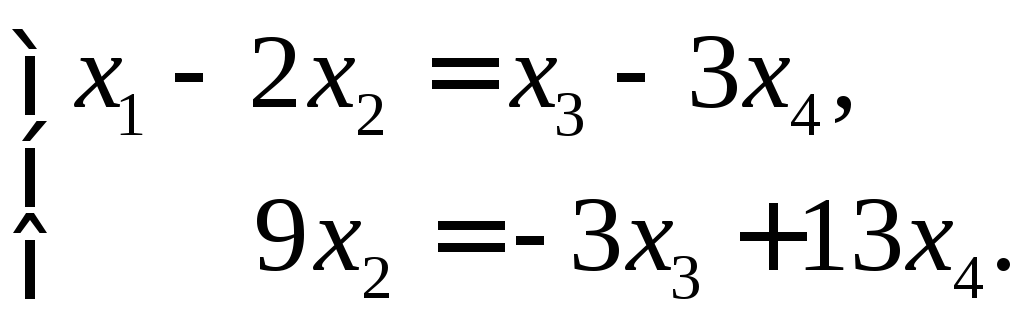Найдём фундаментальную систему решенийэтой системы. Вычтем из второго уравнения первое, умноженное на 4:Перенесёмв правую часть:Переменныездесьсвободные, а переменные–связанные. Придадим свободным переменным значения: вначалезатеми найдёмСоставим таблицу:

1/3		1	0
		0	1

Таким образом, можно считать, что Эти векторы перпендикулярны векторамно не перпендикулярны друг другу. Применим к ним процесс ортогонализации. ПоложимТак как должно бытьтоОтсюда

Таким образом, дополнением векторов до ортогонального базиса будет служить, например, система векторов

>> d=eig(A) %Функция вычисляет собственные значения матрицы A.

>>[U,D]=eig(A) %Матрица U состоит правых собственных векторов, удовлетворяющих соотношению A * U= U * D. Эти векторы нормированы так, что норма каждого из них равна единице.

Упражнение.5

Линейное преобразование, задано в некотором базисе матрицей A. Зная его собственные значения и собственные векторы, найти матрицу из ортонормированных собственных векторовU, проверить ее свойства (является ли матрица ортогональной, если нет, то почему, если да то почему). Проверить результат с помощью функции [U,D]=eig(A) .

, ,,.

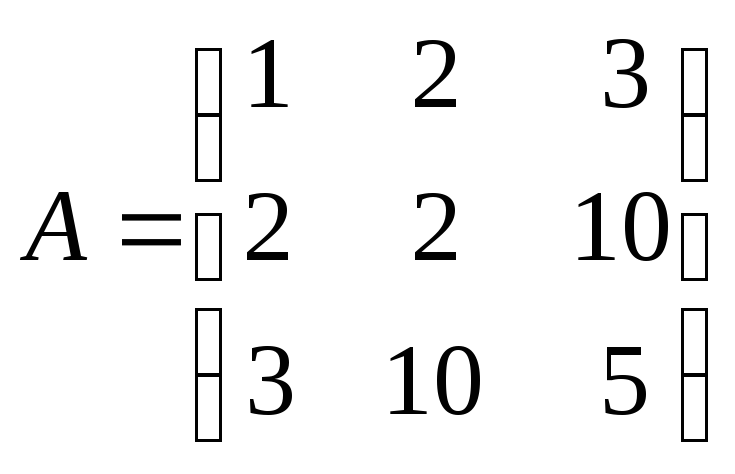Проиллюстрировать задачу.

5. Задание для самостоятельной работы

1. Выполнить в тетради и в MATLAB все упражнения данного практикума.

2. Решить задачи средствами MATLAB.Продумать решения каждой задачи средствами MATLAB. Продумать геометрическую иллюстрацию.

Задачи.

Продумать решения каждой задачи средствами MATLAB. Продумать иллюстрации в MATLAB.

1.Привести матрицулинейного оператора к диагональному виду и найти соответствующий базис. Результаты поверить с помощью функцииeig()

2.Для матрицынайти диагональную матрицуDи унитарную (ортогональную) матрицуUи проверить результат с помощью функцииeig()

3. Найти собственные числа и собственные векторы линейного оператора, заданного матрицей.

Сначала найти на листочке, затем с помощью встроенных команд МАТЛАБ проверить себя.

4.В пространствеL³заданы векторыв некотором базисе. Доказать, что векторысоставляют базис, найти матрицу перехода в базисе, найти координаты векторав базисе..

5.Заданы векторыв некотором базисе. Проверить, что векторысоставляют базис. Применяя процесс ортогонализации Шмидта построить новый ортогональный базис..

Задачу сначала решить на листочке. Опорные вычисления проверяйте на МАТЛАБ. Затем сделать графическую трехмерную иллюстрацию в МАТЛАБ. Изобразите заданные векторы, векторы нового базиса, орты нового базиса, вспомогательные векторы (демонстрирующие процесс ортогонализации). В графическом окне выведите списком, за какие цветные линии - векторы отвечают за те или иные векторы из задачи.