
- •Порядок выполнения.
- •Линейный оператор (линейное преобразование, линейное отображение)
- •Пример. 1. Установить линейность оператора
- •Упражнение. 1
- •Собственные значения и собственные векторы линейного оператора. Характеристическая матрица и характеристический многочлен.
- •Пример 2 ( часть 1) Собственные векторы линейного преобразования
- •Упражнение 2.
- •Упражнение 3.
- •Линейные операторы в пространстве со скалярным произведением. Приведение матрицы линейного преобразования к диагональному виду.
- •Пример 2 (часть 2)Матрица линейного оператора в базисе из собственных векторов.
- •Упражнение 4.
- •Процесс ортогонализации Грама – Шмидта
- •Пример 3. Построение ортонормированного базиса
- •Пример.4 Дополнение системы векторов до ортогонального базиса.
- •Упражнение.5
- •Задание для самостоятельной работы
- •Задачи.
- •Список рекомендуемой литературы
Упражнение 4.
Найти матрицу линейного оператора в базисе из собственных векторов.
![]() ,
,
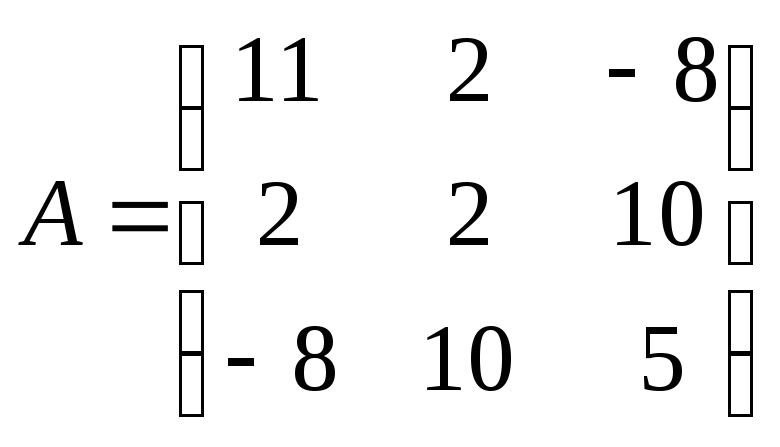 ,
сделать рисунки.
,
сделать рисунки.
Процесс ортогонализации Грама – Шмидта
Матрица ![]() самосопряженного операторавсегдаприводится к диагональному виду. При
этом, используя понятие унитарного
оператора, ее можно представить в виде
самосопряженного операторавсегдаприводится к диагональному виду. При
этом, используя понятие унитарного
оператора, ее можно представить в виде
![]() ,
,
где U– матрица унитарного оператора,
осуществляющего переход от исходного
базиса к базису из собственных векторов
оператора![]() ,
аD– диагональная матрица.
Причем матрицаUсостоит
из нормированных попарно ортогональных
собственных векторов.
,
аD– диагональная матрица.
Причем матрицаUсостоит
из нормированных попарно ортогональных
собственных векторов.
Процесс ортогонализации Шмидта позволяет найти матрицу U.
Базис
![]() евклидова (или унитарного) пространства
называетсяортонормированным
базисом, если он является
ортонормированной системой векторов
этого пространства. Аналогичным образом
определяетсяортогональный базис.
евклидова (или унитарного) пространства
называетсяортонормированным
базисом, если он является
ортонормированной системой векторов
этого пространства. Аналогичным образом
определяетсяортогональный базис.
Ортонормированный
базис евклидова пространства хорош
тем, что вычисление скалярного произведения
и другие вычисления (длины векторов,
расстояния и углы) осуществляются в нём
гораздо проще, чем в произвольном базисе.
Так, например, формула скалярного
произведения в ортогональном базисе
выглядит так:
![]() (формула (1)), в то время как в произвольном
базисе
(формула (1)), в то время как в произвольном
базисе![]() длина вектора в ортонормированном
базисе равна
длина вектора в ортонормированном
базисе равна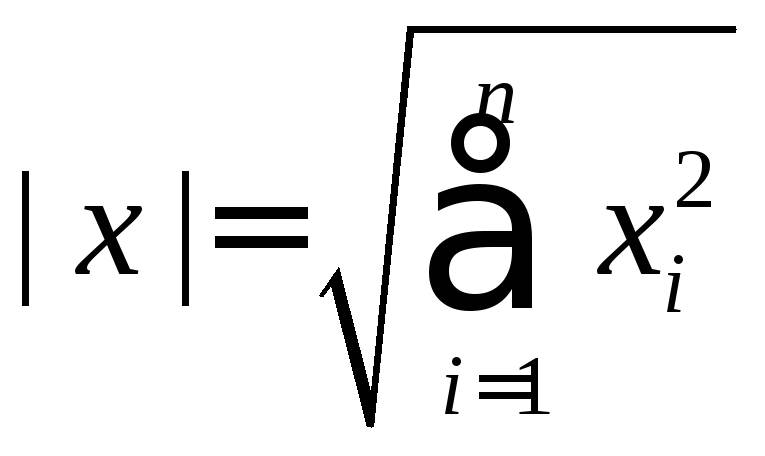 ,
а в произвольном
,
а в произвольном Аналогичная ситуация имеет место в
унитарном пространстве.
Аналогичная ситуация имеет место в
унитарном пространстве.
Оказывается, в любом конечномерном евклидовом или унитарном пространстве существует ортонормированный базис, и для его построения можно использовать процесс ортогонализации, который будет описан ниже. В бесконечномерных пространствах также есть ортонормированные базисы, но доказательство этого утверждения гораздо сложнее, и мы приводить его здесь не будем.
Заметим, что достаточно напучиться строить ортогональный базис, так как ортонормированный из него получается совсем просто. Опишем теперь процесс построения ортогонального базиса евклидова пространства, для унитарного действия точно такие же.
Алгоритм
построения ортогонального базиса. Пусть![]() – произвольный базис евклидова
пространства. Будем строить по нему
ортогональный базис
– произвольный базис евклидова
пространства. Будем строить по нему
ортогональный базис![]()
В качестве первого вектора нового базиса возьмём вектор
 т.е. положим
т.е. положим
Вектор
 будем искать в виде
будем искать в виде ,
и подберём
,
и подберём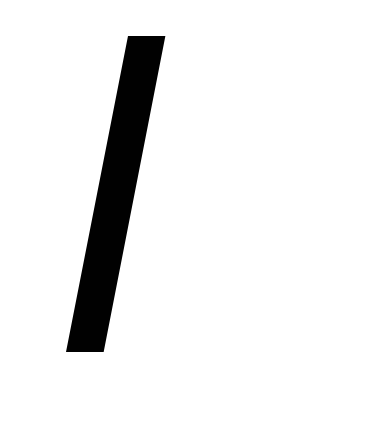 так, чтобы выполнялось условие
так, чтобы выполнялось условие Имеем:
Имеем: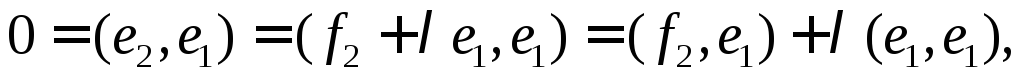 откуда
откуда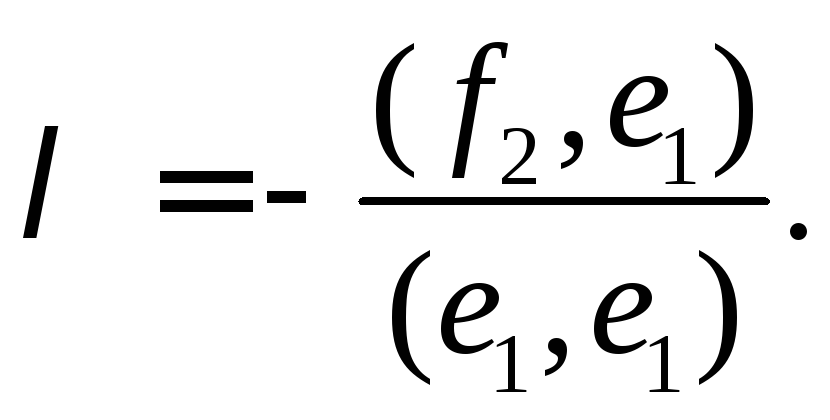
Вектор
 будем искать в виде
будем искать в виде ,
и подберём
,
и подберём так, чтобы выполнялись условия
так, чтобы выполнялись условия
 Имеем:
Имеем: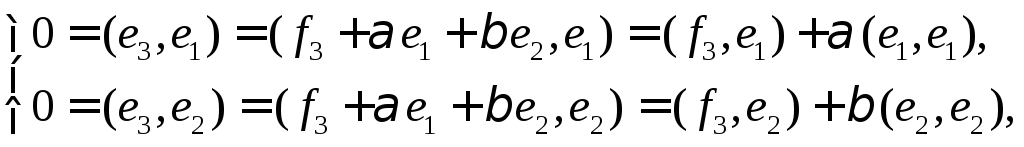 откуда
откуда

Далее будем искать вектор
 в виде
в виде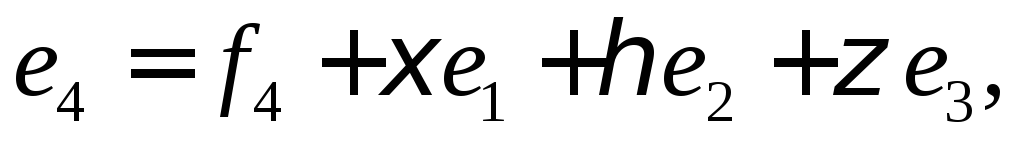 и будем подбирать коэффициенты
и будем подбирать коэффициенты так, чтобы этот вектор был перпендикулярен
векторам
так, чтобы этот вектор был перпендикулярен
векторам
Процесс
завершится построением ортогонального
базиса
![]()
Процесс
ортогонализации имеет прозрачную
геометрическую интерпретацию. А именно,
если в евклидовом пространстве дан
“косой” базис, то мы его “выпрямляем”.
На первый базисный вектор никаких
условий не налагается, поэтому мы берём
![]() Затем среди векторов вида
Затем среди векторов вида![]() (концы этих векторов лежат на прямой,
параллельной вектору
(концы этих векторов лежат на прямой,
параллельной вектору![]() )
мы берём тот единственный, который
перпендикулярен вектору
)
мы берём тот единственный, который
перпендикулярен вектору![]() (см. рис. 1).
(см. рис. 1).

Рис.1.
Затем среди векторов
вида
![]() концы которых лежат на плоскости,
параллельной векторам
концы которых лежат на плоскости,
параллельной векторам![]() и
и![]() выбираем тот единственный, который
перпендикулярен этой плоскости (см.
рис. 2).
выбираем тот единственный, который
перпендикулярен этой плоскости (см.
рис. 2).

Рис.2.
И т.д. В результате
“косой” базис
![]() “выпрямится” до ортогонального
“выпрямится” до ортогонального![]()
Замечание.Этот алгоритм может быть применён и клинейно зависимымвекторам![]() которые базиса не образуют. В этом случае
у нас некоторые из построенных векторов
которые базиса не образуют. В этом случае
у нас некоторые из построенных векторов![]() будут получаться равными 0. Отбрасывая
нулевые векторы, мы получим ортогональный
базис подпространства, натянутого на
векторы
будут получаться равными 0. Отбрасывая
нулевые векторы, мы получим ортогональный
базис подпространства, натянутого на
векторы![]() Кстати говоря, этот алгоритм можно
использовать также для проверки линейной
зависимости или независимости системы
векторов евклидова (или унитарного)
пространства.
Кстати говоря, этот алгоритм можно
использовать также для проверки линейной
зависимости или независимости системы
векторов евклидова (или унитарного)
пространства.
