Пример. 1. Установить линейность оператора
,
то есть проверить
выполнение условий
,
.
Найти образы базисных векторов.
Изобразить каждый вектор и его отображение
на графике. Составить матрицу линейного
оператора.
Создадим м-функцию для оператора, действующего в пространстве Vразмера 4.
function[Y]=operator4(X);
% линейный оператор A(X)=Y;
%A(x1,x2,x3,x4)=(x1+3*x2+2*x3+x4;2*x1+5*x3+2*x4;-1*x2+3*x3+x4;x1+2*x2+x3+3*x4)
Y=[X(1)+3*X(2)+2*X(3)+X(4);2*X(1)+5*X(3)+2*X(4);-1*X(2)+3*X(3)+X(4);X(1)+2*X(2)+X(3)+3*X(4)];
Создадим м-файл.
clear all % очистим все переменные рабочего пространства
help operator4 % получим информацию об операторе
%линейный оператор A(X)=Y;
%A(x1,x2,x3, x4)=(x1+3*x2+2*x3+x4;2*x1+5*x3+2*x4;-1*x2+3*x3+x4;x1+2*x2+x3+3*x4)
% для построения матрицы оператора введите последовательно компоненты базисных вектора
% проверим линейность оператора
% A(x+y)=A(x)+A(y), где x и y - элементы линейного пространства
% A(kx)=kA(x), где k - любое число
syms x1 x2 x3 x4 y1 y2 y3 y4 k
x=[x1;x2; x3;x4], y=[y1;y2;y3;y4];
X=x+y;
[Y12]=operator4(X);
X=x
[Y1]=operator4(X);
X=y;
[Y2]=operator4(X);
isequal (Y12,Y1+Y2) % A(x+y)=A(x)+A(y),
X=k*x;
[Y3]=operator4(X);
Y4=expand(k.*Y1);
isequal (Y3,Y4) % A(kx)=kA(x),
%для построения матрицы оператора
A=zeros(4); % создаем квадратную матрицу из нулей 4-го порядка
% введем последовательно будем воздействовать оператором
%на базисные векторы e1=[1;0;0;0]; e2=[0;1;0;0];e3=[0;0;1;0];e4=[0;0;0;1];
e1=[1;0;0;0]; e2=[0;1;0;0];e3=[0;0;1;0];e4=[0;0;0;1];
X=e1;
[Y]=operator4(X); %воздействуем оператором на X=e1;
% заполняем первый столбец матрицы оператора A
% A(:,1) - так мы выбираем первый столбец матрицы, для операции присвоения столбец Y необходимо превратить в строку
A(:,1)=Y'
X=e2;
[Y]=operator4(X);%воздействуем оператором на X=e2;
A(:,2)=Y' % заполняем второй столбец матрицы оператора A
X=e3;
[Y]=operator4(X); %воздействуем оператором на X=e3;
A(:,3)=Y' % заполняем третий столбец матрицы оператора A
X=e4;
[Y]=operator4(X); %воздействуем оператором на X=e4;
A(:,4)=Y' % заполняем четвертый столбец матрицы оператора A
A % получаем матрицу оператора в базисе {e1, e2, e3, e4}
% проиллюстрируем графически линейность оператора
% A(x+y)=A(x)+A(y)
x=e1; y=e2;
X=x+y;
[Y12]=operator4(X);
X=x
[Y1]=operator4(X);
X=y;
[Y2]=operator4(X);
subplot(1,4,1)
plot([x Y1]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('x ------------ A(x)')
subplot(1,4,2)
plot([y Y2]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('y ------------ A(y)')
subplot(1,4,3)
plot([X Y12]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('x+y ------ A(x+y)')
subplot(1,4,4)
plot([Y12 Y1+Y2]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('A(x)+A(y) = A(x+y)')
Рис. 1
По четвертой картинке видно, что линейность оператора относительно сложения соблюдается.
% A(kx)=kA(x), k - любое число
k=3;
X=k*x;
[Y3]=operator4(X);
subplot(1,3,1)
plot([X Y3]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('k x ------------ A(k x)')
subplot(1,3,2)
plot([x k*Y1]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('x ---------- kA(x)')
subplot(1,3,3)
plot([Y3 k*Y1]','*-','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',6)
title('A(k x) = k A(x)')
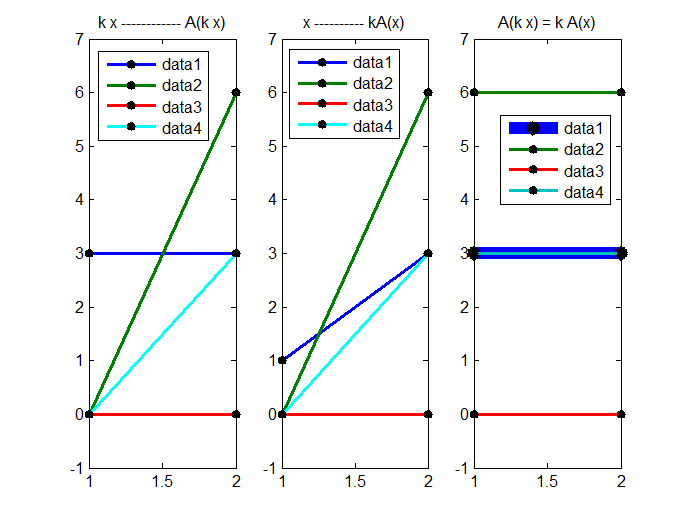
Рис. 2.
По третьей картинке видно, что линейность оператора относительно умножения на число соблюдается. (Третий рисунок справа пришлось править вручную)
Продемонстрируем, как будет выглядеть нелинейный оператор
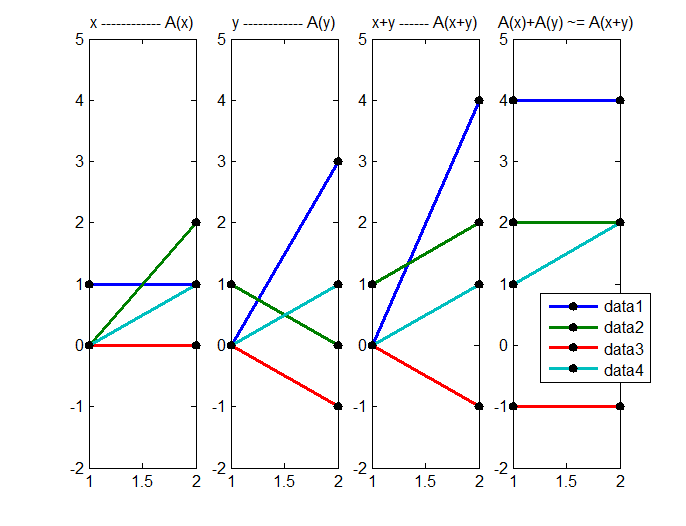
Рис. 3
Мы видим по четвертому графику справа, что линейность относительно сложения по четвертой компоненте не соблюдается.
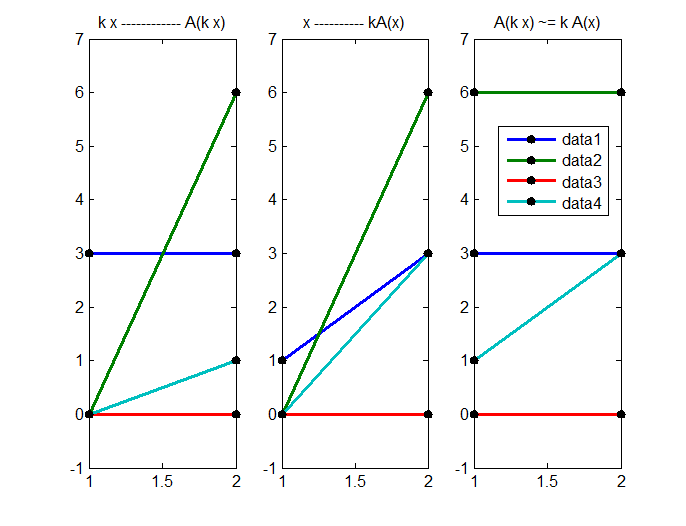
Рис. 4
По третьей картинке справа мы видим, что линейность относительно умножения на число также не соблюдается по 4-ой компоненте.