Упражнение 12 (б) *. Приведение уравнения кривой второго порядка к каноническому виду.
Нарисовать кривую, заданную уравнением
С помощью реализованной ранее функции get_canonicalпривести уравнение данной кривой к каноническому виду, отметить фокусы, отобразить директрисы. Сравнить результат.
[u, v] = get_canonical(1, 1, 2);
syms x y;
c=sqrt(1/u-1/v);
a=sqrt(1/u);
D=a^2/c;
ezplot(x^2+x*y+2*y^2-1);
hold on;
grid on;
plot(-c,0,'*r');
plot(c,0,'*r');
line([D D],[-10 10]);
line([-D -D],[-10 10]);
Упражнение 13. Изобразить часть эллипсоида лежащего в первом октанте
Используя данную программу изобразите
часть эллипсоида лежащего в первом
октанте (
,
верхнюю часть эллипсоида
,
изобразите также эллипсоид в декартовых
координатах, используя «meshgrid»
и «mesh» или «plot3».
Сравните полученные результаты.
>> a = 1; b = 4; c = 1;
>> theta = [0 : pi/100 : pi/2]'; phi = [0 : pi/100 : pi/2];
>> x = a*cos(theta)*cos(phi);
>> y = b*cos(theta)*sin(phi);
>> z = c*sin(theta)*ones(size(phi));
>> figure('Color', 'w')
>> mesh(x, y, z);
>> xlabel('x'), ylabel('y'), zlabel('z')
>> theta = [0 : pi/50 : pi/2]'; phi = [0 : pi/200 : 2*pi];
>> x = a*cos(theta)*cos(phi);
>> y = b*cos(theta)*sin(phi);
>> z = c*sin(theta)*ones(size(phi));
>> figure('Color', 'w')
>> mesh(x, y, z);
>> xlabel('x'), ylabel('y'), zlabel('z')
>> theta = [-pi/2 : pi/50 : pi/2]'; phi = [0 : pi/100 : 2*pi];
>> x = a*cos(theta)*cos(phi);
>> y = b*cos(theta)*sin(phi);
>> z = c*sin(theta)*ones(size(phi));
>> figure('Color', 'w')
>> mesh(x, y, z);
>> xlabel('x'), ylabel('y'), zlabel('z')
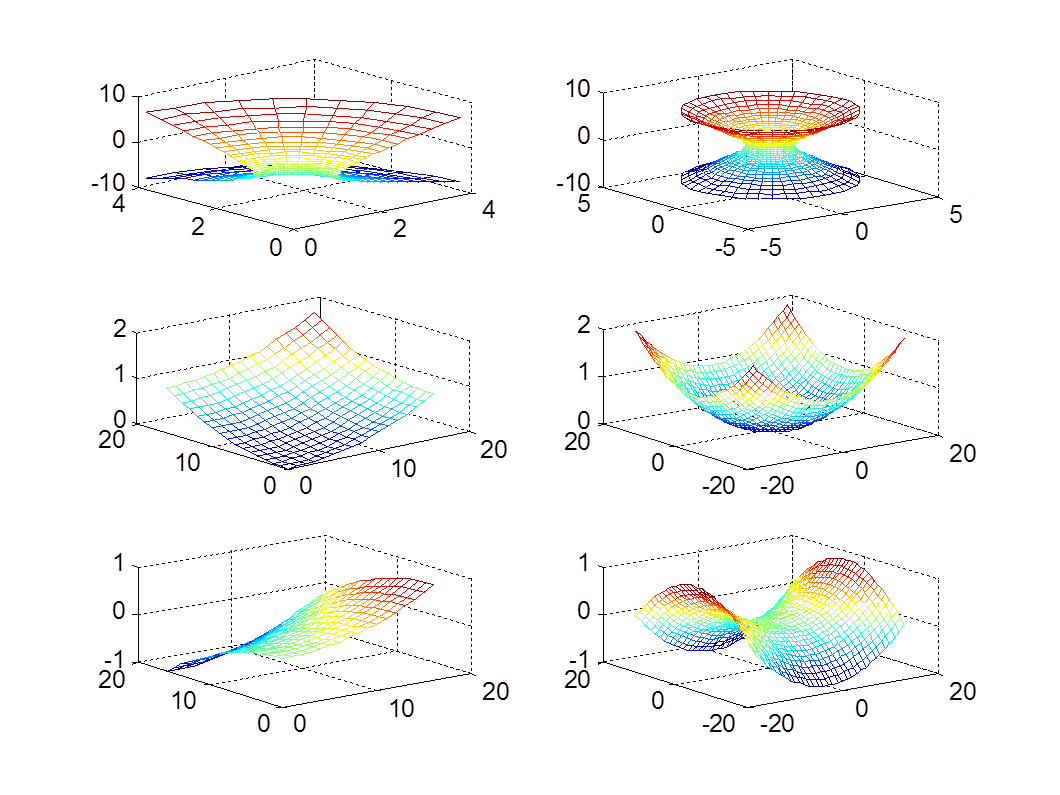
Упражнение 14 – 15. Провести исследование поверхностей второго порядка методом сечений.
Однополосного гиперболоида, двуполостного гиперболоида, гиперболического параболоида, эллиптического параболоида.
Например, по однополостному параболоиду должно быть примерно такое исследование:
разбиваем графическое окно на несколько подобластей
в первом рисуем все, что касается сечений параллельных плоскости УОХ,
во втором ... ZOX,
в третьей ZOY
Прокомментировать, как получаемые сечения связаны с непосредственным названием фигуры.
>> subplot(3, 2, 1);
>> a = 1; b = 1; c = 2;
>> u = [-2 : 1/10 : 2]'; phi = [0 : pi/20 : pi/2];
>> x = a*cosh(u)*cos(phi);
>> y = b*cosh(u)*sin(phi);
>> z = c*sinh(u)*ones(size(phi));
>> mesh(x, y, z);
>> subplot(3, 2, 2);
>> a = 1; b = 1; c = 2;
>> u = [-2 : 1/10 : 2]'; phi = [0 : pi/20 : 2*pi];
>> x = a*cosh(u)*cos(phi);
>> y = b*cosh(u)*sin(phi);
>> z = c*sinh(u)*ones(size(phi));
>> mesh(x, y, z);
>> subplot(3, 2, 3);
>> a = 16; b = 16;
>> [x, y] = meshgrid([0 : 1 : a], [0 : 1 : b]);
>> z = ((x.^2)/(a^2)+(y.^2)/(b^2));
>> mesh(x, y, z);
>> subplot(3, 2, 4);
>> a = 16; b = 16;
>> [x, y] = meshgrid([-a : 1 : a], [-b : 1 : b]);
>> z = ((x.^2)/(a^2)+(y.^2)/(b^2));
>> mesh(x, y, z);
>> subplot(3, 2, 5);
>> a = 16; b = 16;
>> [x, y] = meshgrid([0 : 1 : a], [0 : 1 : b]);
>> z = ((x.^2)/(a^2)-(y.^2)/(b^2));
>> mesh(x, y, z);
>> subplot(3, 2, 6);
>> a = 16; b = 16;
>> [x, y] = meshgrid([-a : 1 : a], [-b : 1 : b]);
>> z = ((x.^2)/(a^2)-(y.^2)/(b^2));
>> mesh(x, y, z);
Упражнение 16. Сделать анимацию, вращения прямой вокруг параллельной ей прямой.
Прямая L– прямая параллельная осиOX
OX – ось,вокруг которой вращается прямаяL. (Что получится?)
clf; xyz; grid on, holdon, boxon, axisequal,view(120,10)
% Строим ось вращения на основе параметрического задания прямой
% t-параметр, М-точка, принадлежащая оси,
% V=[1;0;0] – направляющий вектор оси
t=[-1 3]; M=[0;2.5;2.5]; V=[1;0;0];
os=M*ones(size(t))+V*t;
plot3(os (1,:), os (2,:), os (3,:),'Color','red','LineWidth',2);
% Строим образующую L на основе параметрического задания прямой
% t-параметр тот же, М-точка та же, принадлежащая прямой,
% V =[0;1;1]– направляющий вектор прямой
M=[0;1;1]; V=[1;0;0];
obr=M*ones(size(t))+V*t;
L=plot3(obr (1,:), obr (2,:), obr (3,:));
fori=1:2:360
L=plot3(obr (1,:), obr (2,:), obr (3,:),'g');
rotate(L,[1 0 0],10+i);
pause(0.01);
end
