Упражнение 3.
Доказать, что уравнение
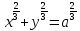представляет
собой алгебраическую кривую шестого
порядка
.
Упражнение 4. Построение полярной розы.
Напишите подобную программу, для
.
a = 1; n = 4;
phi=0:pi/100:2*pi;
r=a*sin(n*phi);
r=max(0,r);
set(polar(phi, r,'r'),'LineWidth',2);
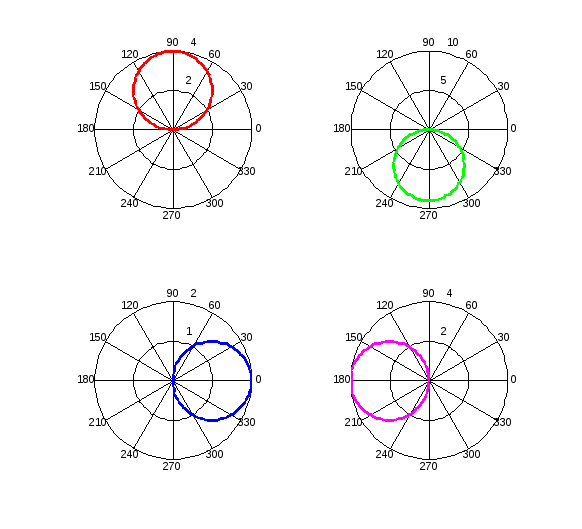
Упражнение 5. Уравнения однолепестковых роз в полярной системе координат.
Построить графики в полярных координатах
с помощью функции polar
.
Сравните полученные результаты с
результатами упражнения 2.
phi=0:pi/100:2*pi;
subplot(2,2,1);
r=max(0,4*sin(phi));
set(polar(phi, r,'r'),'LineWidth',2, 'Color', 'red');
subplot(2,2,2);
r=max(0,-9*sin(phi));
set(polar(phi, r,'r'),'LineWidth',2, 'Color', 'green');
subplot(2,2,3);
r=max(0,2*cos(phi));
set(polar(phi, r,'r'),'LineWidth',2, 'Color', 'blue');
subplot(2,2,4);
r=max(0,-4*cos(phi));
set(polar(phi, r,'r'),'LineWidth',2, 'Color', 'magenta');
Упражнение 6. Линии в декартовых и полярных координатах.
Построить линии
,
,
в декартовой системе координат с помощью
различных команд. Перейти к полярной
системе координат, построить линии в
полярных координатах с помощью функции
«polar». Сравнить,
прокомментировать полученные результаты.
x_min = -2; x_max = 2; y_min = -2; y_max = 2;
grid on; hold on; axis equal; axis([x_min x_max y_min y_max])
% Рисуем оси координат и подписываем их
line([x_min x_max],[0 0],'Color','black', 'LineStyle', '-');
line([0 0],[y_min y_max],'Color','black', 'LineStyle', '-');
text(x_max+0.1, 0, 'X', 'FontSize', 10);
text(0+0.1, y_max-0.2, 'Y', 'FontSize', 10);
set(ezplot('x.^2+y.^2=1'),'Color', 'red');
set(ezplot('x+0.*y=1'),'Color', 'green');
set(ezplot('0.*x+y=1'),'Color', 'blue');
polar(0, 1.5); hold on;
set(ezplot('x.^2+y.^2=1'),'Color', 'red');
set(ezplot('x+0.*y=1'),'Color', 'green');
set(ezplot('0.*x+y=1'),'Color', 'blue');
Упражнение 7. Параллельный перенос осей координат
Создать код, с помощью которого
производится сдвиг (параллельный
перенос) на
относительно оси абсцисс и на
относительно оси ординат графика функции
.
Координаты сдвига сделать входящими
параметрами.
xm = 10; ym = 5
x = [-10:0.1:10]; y = -3*x+2;
function [] = move(x, y, xm, ym)
%Cдвиг графика функции
x1 = x1+xm;
y1 = y1+ym;
hold on, grid on, axis equal
plot(x, y, 'r'), plot(x1, y1, 'g')
end
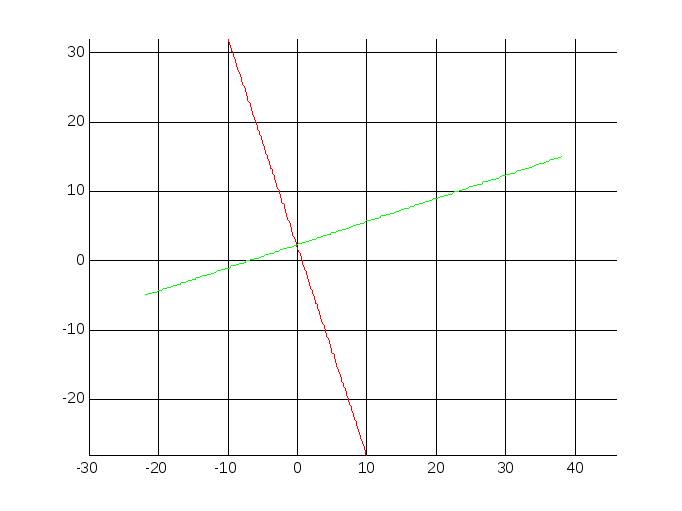
Упражнение 8. Поворот и параллельный перенос осей координат
Создать код, с помощью которого
производится поворот на угол исдвиг (параллельный перенос) на
относительно оси абсцисс и на
относительно оси ординат графика функции
.
Координаты сдвига и угол поворота
сделать входящими параметрами.
phi =pi/2; xm = 10; ym = 5
x = [-10:0.1:10]; y = -3*x+2;
function [] = rotate_and_move(x, y, phi, xm, ym)
%Поворот и сдвиг графика функции
x1 = x.*cos(phi)-y.*sin(phi);
y1 = x.*sin(phi)+y.*cos(phi);
x1 = x1+xm;
y1 = y1+ym;
hold on, grid on, axis equal
plot(x, y, 'r'), plot(x1, y1, 'g')
end
Упражнение 9. Уравнение окружностей со смещенным центром.
Составить уравнение окружности с заданным центром и радиусом.
.
Изобразить при помощиezplot. Добавить оси симметрии.
Создать 4 графические подобласти.
В первой построить верхнюю часть окружности с помощью функции plot, соответствующим образом выразивy.
Во второй построить нижнюю часть окружности с помощью функции plot,соответствующим образом выразивy.
В третьей построить правую часть окружности с помощью функции plot, соответствующим образом выразивx.
В четвертой построить левую часть окружности с помощью функции plot,соответствующим образом выразивx.
A) M(0,0), R=4; C) M(-7,7), R=9; E) M(3,0), R=3
B) M(5,5), R=4; D) M(3,-3), R=1; F) M(-2,0), R=2
>> subplot(2, 3, 1)
>> lab_1_4_u_9_1([0, 0], 4, [])
>> subplot(2, 3, 2)
>> lab_1_4_u_9_1 ([-7, 7], 9, [-16, 16])
>> subplot(2, 3, 3)
>> lab_1_4_u_9_1 ([3, 0], 3, [])
>> subplot(2, 3, 4)
>> lab_1_4_u_9_1 ([5, 5], 4, [-9, 9])
>> subplot(2, 3, 5)
>> lab_1_4_u_9_1 ([3, -3], 1, [])
>> subplot(2, 3, 6)
>> lab_1_4_u_9_1 ([-2, 0], 2, [])
>> figure
>> lab_1_4_u_9_2 ([0, 0], 4)
>> figure
>> lab_1_4_u_9_2 ([5, 5], 4)
>> figure
>> lab_1_4_u_9_2 ([-7, 7], 9)
>> figure
>> lab_1_4_u_9_2 ([3, -3], 1)
>> figure
>> lab_1_4_u_9_2 ([3, 0], 3)
>> figure
>> lab_1_4_u_9_2 ([-2, 0], 2)
Код функции lab_1_4_u_9_1:
function [] = lab_1_4_u_9_1 (M, R, args)
syms x y;
if (length(args) >= 2)
ezplot((x-M(1)).^2+(y-M(2)).^2-R.^2, args)
else
ezplot((x-M(1)).^2+(y-M(2)).^2-R.^2)
end
line([M(1); M(1)], [-20; 20])
line([-20; 20], [M(2); M(2)])
grid on, axis equal;
end
Код функции lab_1_4_u_9_2:
function [] = lab_1_4_u_9_2 (M, R)
x = [M(1)-R : 0.01 : M(1)+R];
y = [M(2)-R : 0.01 : M(2)+R];
x1 = sqrt(R.^2-(y-M(2)).^2)+M(1);
x2 = -sqrt(R.^2-(y-M(2)).^2)+M(1);
y1 = sqrt(R.^2-(x-M(1)).^2)+M(2);
y2 = -sqrt(R.^2-(x-M(1)).^2)+M(2);
ax = [M(1)-R, M(1)+R, M(2)-R, M(2)+R];
subplot(2, 2, 1);
plot(x, y1);
grid on, axis equal, axis(ax);
subplot(2, 2, 2);
plot(x, y2);
grid on, axis equal, axis(ax);
subplot(2, 2, 3);
plot(x1, y);
grid on, axis equal, axis(ax);
subplot(2, 2, 4);
plot(x2, y);
grid on, axis equal, axis(ax);
end
