Лабораторная работа №6 Ярослав Ермилов (МП-14)

Лабораторная работа №6

Линейные операторы. Собственные числа и собственные значения линейных операторов

Работу выполнил: Ермилов Ярослав (МП-14)

Упражнение 1.

Установить какие из заданных линейных операторов являются линейными, то есть проверить выполнение условий , . Сделать иллюстрации. Для линейных операторов составить матрицу линейного отображения.

1)

2)

3)

% Проверим линейность оператора

% A(x+y) = A(x)+A(y), где x и y - элементы линейного пространства

% A(k*x) = k*A(x), где k - любое число

syms x1 x2 x3 x4 y1 y2 y3 y4 k

x = [x1;x2;x3;x4]; y = [y1;y2;y3;y4];

[X]=operator3(x);

[Y]=operator3(y);

[X_plus_Y]=operator3(x+y);

isEqual_sum = isequal(X_plus_Y,X+Y) % A(x+y)=A(x)+A(y)

[kX]=operator3(k*x);

k_X=expand(k.*X);

isEqual_kA = isequal(kX,k_X) % A(kx)=kA(x)

if (isEqual_sum == 1 && isEqual_kX == 1)

display('Оператор явлется линейным');

else

display('Оператор не явлется линейным');

end;

Упражнение 2.

Найти собственные векторы и собственные значения линейного оператора A, заданного в некотором базисе матрицей: , создать алгоритм в MATLAB, соответствующий алгоритму решения задачи из примера 2. С помощью команд eig(A) и isequal() осуществить проверку найденных собственных значений. Проиллюстрируйте задачу в MATLAB, как на рис. 5.

function lab_2_2_u_2(A)

syms x x1 x2;

X = [x, 0; 0, x];

A1 = A-X;

x1 = det(A1);

X = solve(x1, x)

yr1 = A(1, 1)*x1+A(1, 2)*x2;

yr1 = subs(yr1, x1, 1);

Y1 = [1, 0];

Y1(2) = solve(yr1, x2);

Y1

yr2 = A(2, 1)*x1+A(2, 2)*x2;

yr2 = subs(yr2, x1,1);

Y2 = [1, 0];

Y2(2) = solve(yr2, x2);

Y2

hold on, grid on;

quiver(0, 0, 1, 0, 1, 'k');

quiver(0, 0, 0, 1, 1, 'k');

quiver(0, 0, A(1, 1), A(2, 1), 1, 'r');

quiver(0, 0, A(1, 2), A(2, 2), 1, 'b');

text(-0.1, 0.5, '\bfe2');

text(0.5, -0.25, '\bfe1');

end

>> A = [1, 1; 0, 2];

>> lab_2_2_u_2(A)

X =

[1]

[ ]

[2]

Y1 =

1 -1

Y2 =

1 0

Упражнение 3

Найти собственные векторы линейного оператора A, заданного в некотором базисе матрицей: , с помощью команды eig(A) можно найти собственные значения. Создайте матрицы вида состоящие из собственного вектора и его образа.

Постройте графики, иллюстрирующие векторы и их отображения, как на рис. 6.

function lab_2_2_u_3(A)

syms x x1 x2 x3;

D = eig(A);

x = [x1, x2, x3];

for i = [1 : 3]

yr = A(i, 1)*x1+A(i, 2)*x2+A(i, 3)*x3;

if (i == 2)

yr = subs(yr, x(1), 1);

yr = subs(yr, x(3), 1);

end

if (i == 1)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(3), 1);

end

if (i == 3)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(1), 1);

end

Y = [1, 0];

u = x(i);

Y(2) = solve(yr, u);

Vi = horzcat(D(i), Y)

subplot(1, 3, i);

hold on, grid on;

plot(Vi', '*-', 'LineWidth', 2, 'MarkerEdgeColor','k', ...

'MarkerFaceColor', 'g', 'MarkerSize', 6)

end

end

>> A = [11, 2, -8; 2, 2, 10; -8, 10, 5];

>> lab_2_2_u_3(A)

Vi =

-9.0000 1.0000 0.5455

Vi =

9.0000 1.0000 -6.0000

Vi =

18.0000 1.0000 -0.4000

Упражнение 4

Найти матрицу линейного оператора в базисе из собственных векторов.

, , сделать рисунки.

function lab_2_2_u_4(A)

syms x x1 x2 x3;

S = size(A);

n = S(1);

D = zeros(n);

D1 = eig(A);

x = [x1, x2, x3];

b = [];

figure;

for i = [1 : n]

if (n == 3)

yr = A(i, 1)*x1+A(i, 2)*x2+A(i, 3)*x3;

if (i == 2)

yr = subs(yr, x(1), 1);

yr = subs(yr, x(3), 1);

Y = [1, 0, 1];

D(i, i) = D1(i);

u = x(i);

Y(i) = solve(yr, u);

b = vertcat(b, Y);

end

if (i == 1)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(3), 1);

Y = [0, 1, 1];

D(i, i) = D1(i);

u = x(i);

Y(i) = solve(yr, u);

b = vertcat(b, Y);

end

if (i == 3)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(1), 1);

Y = [1, 1, 0];

D(i, i) = D1(i);

u = x(i);

Y(i) = solve(yr, u);

b = vertcat(b, Y);

end

hold on, grid on;

if (i == 1)

v = 'r';

elseif (i == 2)

v = 'c';

else

v = 'g';

end

quiver3(0, 0, 0, D(i, i)*b(i, 1), ...

D(i, i)*b(i, 2), D(i, i)*b(i, 3), 1, v);

quiver3(0, 0, 0, b(i, 1), b(i, 2), ...

b(i, 3), 1, 'k', 'linewidth', 2);

end

if (n == 2)

yr = A(i, 1)*x1+A(i, 2)*x2;

if (i == 2)

yr = subs(yr, x(1), 1);

Y = [1, 0];

D(i, i) = D1(i);

u = x(i);

Y(i) = solve(yr, u);

b = vertcat(b, Y);

end

if (i == 1)

yr = subs(yr, x(2), 1);

Y = [0, 1];

D(i, i) = D1(i);

u = x(i);

Y(i) = solve(yr, u);

b = vertcat(b, Y);

end

hold on, grid on;

if (i == 1)

v = 'r';

else

v = 'g';

end

quiver(0, 0, D(i, i)*b(i, 1), ...

D(i, i)*b(i, 2), 1, v, 'linewidth', 3);

quiver(0, 0, b(i, 1), b(i, 2), ...

1, 'k', 'linewidth', 2);

end

end

D

End

>> A = [1, 1; 0, 2]; B = [11, 2, -8; 2, 2, 10; -8, 10, 5];

>> lab_2_2_u_4(A), lab_2_2_u_4 (B)

D =

1 0

0 2

D =

-9.0000 0 0

0 9.0000 0

0 0 18.0000

Упражнение 5

Линейное преобразование, задано в некотором базисе матрицей A. Зная его собственные значения и собственные векторы, найти матрицу из ортонормированных собственных векторов U, проверить ее свойства (является ли матрица ортогональной, если нет, то почему, если да, то почему). Проверить результат с помощью функции .

, , , .

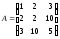Проиллюстрировать задачу.

function A1 = lab_2_2_u_5(A)

syms x x1 x2 x3;

S = size(A);

n = S(1);

x = [x1, x2, x3];

b = [];

for i = [1 : n]

if (n == 2)

yr = A(i, 1)*x1+A(i, 2)*x2;

if (i == 1)

yr = subs(yr, x(2), 1);

Y = [0, 1];

u = x(i);

Y(i) = solve(yr, u);

Y(i) = Y(i)';

b = vertcat(b, Y);

end

if (i == 2)

yr = subs(yr, x(1), 1);

Y = [1, 0];

u = x(i);

Y(i) = solve(yr, u);

Y(i) = Y(i)';

b = vertcat(b, Y);

f1 = b(1, :);

f2 = b(2, :);

e1 = f1;

a = -(dot(f2, e1)/dot(e1, e1));

e2 = f2+a*e1;

A1 = vertcat(e1, e2);

end

end

if (n == 3)

yr = A(i, 1)*x1+A(i, 2)*x2+A(i, 3)*x3;

if (i == 1)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(3), 1);

Y = [0; 1; 1];

u = x(i);

Y(i) = solve(yr, u);

Y(i) = Y(i)';

b = horzcat(b, Y);

end

if (i == 2)

yr = subs(yr, x(1), 1);

yr = subs(yr, x(3), 1);

Y = [1; 0; 1];

u = x(i);

Y(i) = solve(yr, u);

Y(i) = Y(i)';

b = horzcat(b, Y);

end

if (i == 3)

yr = subs(yr, x(2), 1);

yr = subs(yr, x(1), 1);

Y = [1; 1; 0];

u = x(i);

Y(i) = solve(yr, u);

Y(i) = Y(i)';

b = horzcat(b, Y);

f1 = b(1, :);

f2 = b(2, :);

f3 = b(3, :);

e1 = f1;

a = -(dot(f2, e1)/dot(e1, e1));

e2 = f2+a*e1;

A1 = vertcat(e1, e2);

a = -(dot(f3, e1)/dot(e1, e1));

b = -(dot(f3, e2)/dot(e2, e2));

e3 = f3+b*e2+a*e1;

A1 = vertcat(A1, e3);

end

end

end

end

>> A = [1, 2; 5, 4]; B = [1, 2; 2, 3];

>> C = [1, 2, 3; 2, 2, 10; 3, 10, 5];

>> D = [1, 1, 3; 1, 5, 1; 3, 1, 1];

>> lab_2_2_u_5(A)

ans =

-2.0000 1.0000

-0.3000 -0.6000

>> lab_2_2_u_5(B)

ans =

-2.0000 1.0000

-0.0667 -0.1333

>> lab_2_2_u_5(C)

ans =

-5.0000 1.0000 1.0000

-0.8519 -5.6296 1.3704

-0.4717 -0.4043 -1.9542

>> lab_2_2_u_5(D)

ans =

-4.0000 1.0000 1.0000

0.2444 -0.2111 1.1889

0.2050 0.7321 0.0878

-10- 21.07.2019