Лабораторная работа №1_1

Работу выполнил: Ермилов Ярослав (МП-14)

Упражнение 2. Форматы вывода результата вычислений.

1) сложите два числа 1/2 и 2/3 и определите формат полученного ответа;

>> 1/2 + 2/3

ans = 1.1667

2) перейдите в формат format rational (Можно кратко в format rat) и сложите числа 1/2 и 2/3, а также числа 0.3 и 0.6, затем все тоже проделайте в форматах shortE, longE;

>> format rat

>> 1/2 + 2/3

ans = 7/6

>> 0.3+0.6

ans = 9/10

>> format shortE

>> 1/2 + 2/3

ans = 1.1667e+000

>> 0.3+0.6

ans = 9.0000e-001

>> format longE

>> 1/2 + 2/3

ans = 1.166666666666667e+000

>> 0.3+0.6

ans = 8.999999999999999e-001

1.7. Символьные переменные. Работа с алгебраическими выражениями.

>> f=(x+1)*(x-1)

>> f=collect(f)

f = x^2 – 1

Ответьте в отчете на вопрос, что сделала команда «collect» с выражением f ?

Функция «collect» упростила выражение

Упражнение 4.. Различные способы задания векторов.

1) Задать вектор-строку с помощью

a) ввода чисел c пробелами;

>> a = [1 2 3 4 5]

a = 1 2 3 4 5

b) ввода чисел с запятыми;

>> a = [1, 2, 3, 4, 5]

a = 1 2 3 4 5

c) стандартной функцией horzcat(, , , )

>> a = horzcat(1,2,3,4,5)

a = 1 2 3 4 5

d) двоеточия «:» с шагом можно задать те же числа от 1 до 6 с шагом 1

>> a = [1:6]

a = 1 2 3 4 5 6

2) Задать вектор-столбец с помощью

a) точки запятой «;» ;

>> b = [1;1.9;2.8;3.7]

b =

1.0000

1.9000

2.8000

3.7000

b) транспонировав вектор-строку, с помощью символа «'» - одинарная кавычка (буква э в латинском регистре)

>> b = [1,1.9,2.8,3.7]'

b =

1.0000

1.9000

2.8000

3.7000

с) стандартной функцией vertcat(, , ,)

>> b = vertcat(1,1.9,2.8,3.7)

b =

1.0000

1.9000

2.8000

3.7000

d) двоеточия «:» с шагом и транспонирования «'».

>> b = [1:0.9:3.7]'

b =

1.0000

1.9000

2.8000

3.7000

Упражнение 5.

1. Вычислите сумму массивов и 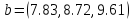, запишите результат в массив  с1,  и выведите все векторы в командное окно.

>> a = [1.2, 5.3, 6.4]

a = 1.2000 5.3000 6.4000

>> b = [7.83, 8.72, 9.61]

b = 7.8300 8.7200 9.6100

>> c1 = a + b

c1 = 9.0300 14.0200 16.0100

2. Найдите разность b и a, результат запишите в c2  и выведите его в командное окно.

>> c2 = b-a

c2 = 6.6300 3.4200 3.2100

Упражнение 6.

Для матриц , , , , , , , (ввести символьно соответствующие элементы: syms a11 a12 и тд.), осуществить операции:

A' % эрмитово сопряжение

A.' % транспонирование

B' % эрмитово сопряжение

B.' % транспонирование

% умножение на число:

A1 = 2*A, A2=A*3, A3=4.*A, A4=A*.5

% сложение матриц:

C1 = A+B, C2=A+D2, C3=B+D1, C4=A+E2, C5=B+C1

%умножение матриц:

% что меняет умножение квадратной матрицы на единичную E?

F1 = A*B, F2=B*A, F3=B' *A', F=F1*F1*F1

% поэлементное умножение матриц:

C = A.*D2

% возведение матрицы А в степень, (то же что и B=A*A, выполнимо только для квадратных матриц)

A^2 % невыполнимо

F1^2 % выполнимо

A.^2 % возведение каждого элемента матрицы А в степень

>> syms a11; syms a12; syms a13; syms a21; syms a22; syms a23

>> A = [a11, a12, a13; a21, a22, a23]

A =

[ a11, a12, a13]

[ a21, a22, a23]

>> syms b11; syms b12; syms b21; syms b22; syms b31; syms b32

>> B = [b11, b12; b21, b22; b31, b32]

B =

[ b11, b12]

[ b21, b22]

[ b31, b32]

>> c=2, D1=ones(2,3), D2=ones(3,2),E1=eye(2,3), E2=eye(3,2), E3=eye(3)

c = 2

D1 =

1 1 1

1 1 1

D2 =

1 1

1 1

1 1

E1 =

1 0 0

0 1 0

E2 =

1 0

0 1

0 0

E3 =

1 0 0

0 1 0

0 0 1

>> A'

ans =

[ conj(a11), conj(a21)]

[ conj(a12), conj(a22)]

[ conj(a13), conj(a23)]

>> A.'

ans =

[ a11, a21]

[ a12, a22]

[ a13, a23]

>> B'

ans =

[ conj(b11), conj(b21), conj(b31)]

[ conj(b12), conj(b22), conj(b32)]

>> B.'

ans =

[ b11, b21, b31]

[ b12, b22, b32]

>> A1 = 2*A, A2=A*3, A3=4.*A, A4=A*.5

A1 =

[ 2*a11, 2*a12, 2*a13]

[ 2*a21, 2*a22, 2*a23]

A2 =

[ 3*a11, 3*a12, 3*a13]

[ 3*a21, 3*a22, 3*a23]

A3 =

[ 4*a11, 4*a12, 4*a13]

[ 4*a21, 4*a22, 4*a23]

A4 =

[ a11/2, a12/2, a13/2]

[ a21/2, a22/2, a23/2]

>> C1 = A+B

Error in MuPAD command: Array sizes must match.

Данная ошибка сообщает нам о том, что выполнить сложение двух матриц разного размера невозможно. Поэтому, для того чтобы сложить матрицы А и В можно транспонировать одну из них, например А:

>> A = A.'

A =

[ a11, a21]

[ a12, a22]

[ a13, a23]

>> C1 = A+B

C1 =

[ a11 + b11, a21 + b12]

[ a12 + b21, a22 + b22]

[ a13 + b31, a23 + b32]

>> C2=A+D2

C2 =

[ a11 + 1, a21 + 1]

[ a12 + 1, a22 + 1]

[ a13 + 1, a23 + 1]

Чтобы сложить матрицы B и D1 можно транспонировать одну из них, например D1:

>> C3=B+D1.'

C3 =

[ b11 + 1, b12 + 1]

[ b21 + 1, b22 + 1]

[ b31 + 1, b32 + 1]

>> C4=A+E2

C4 =

[ a11 + 1, a21]

[ a12, a22 + 1]

[ a13, a23]

>> C5=B+C1

C5 =

[ a11 + 2*b11, a21 + 2*b12]

[ a12 + 2*b21, a22 + 2*b22]

[ a13 + 2*b31, a23 + 2*b32]

>> F1 = A*B

F1 =

[ a11*b11 + a12*b21 + a13*b31, a11*b12 + a12*b22 + a13*b32]

[ a21*b11 + a22*b21 + a23*b31, a21*b12 + a22*b22 + a23*b32]

>> F2=B*A

F2 =

[ a11*b11 + a21*b12, a12*b11 + a22*b12, a13*b11 + a23*b12]

[ a11*b21 + a21*b22, a12*b21 + a22*b22, a13*b21 + a23*b22]

[ a11*b31 + a21*b32, a12*b31 + a22*b32, a13*b31 + a23*b32]

>> F3=B' *A'

F3 =

[ conj(a11)*conj(b11) + conj(a12)*conj(b21) + conj(a13)*conj(b31), conj(a21)*conj(b11) + conj(a22)*conj(b21) + conj(a23)*conj(b31)]

[ conj(a11)*conj(b12) + conj(a12)*conj(b22) + conj(a13)*conj(b32), conj(a21)*conj(b12) + conj(a22)*conj(b22) + conj(a23)*conj(b32)]

>> F=F1*F1*F1

F =

[ ((a11*b11 + a12*b21 + a13*b31)*(a11*b12 + a12*b22 + a13*b32) + (a11*b12 + a12*b22 + a13*b32)*(a21*b12 + a22*b22 + a23*b32))*(a21*b11 + a22*b21 + a23*b31) + ((a11*b11 + a12*b21 + a13*b31)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31))*(a11*b11 + a12*b21 + a13*b31), ((a11*b11 + a12*b21 + a13*b31)*(a11*b12 + a12*b22 + a13*b32) + (a11*b12 + a12*b22 + a13*b32)*(a21*b12 + a22*b22 + a23*b32))*(a21*b12 + a22*b22 + a23*b32) + ((a11*b11 + a12*b21 + a13*b31)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31))*(a11*b12 + a12*b22 + a13*b32)]

[ ((a11*b11 + a12*b21 + a13*b31)*(a21*b11 + a22*b21 + a23*b31) + (a21*b11 + a22*b21 + a23*b31)*(a21*b12 + a22*b22 + a23*b32))*(a11*b11 + a12*b21 + a13*b31) + ((a21*b12 + a22*b22 + a23*b32)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31))*(a21*b11 + a22*b21 + a23*b31), ((a11*b11 + a12*b21 + a13*b31)*(a21*b11 + a22*b21 + a23*b31) + (a21*b11 + a22*b21 + a23*b31)*(a21*b12 + a22*b22 + a23*b32))*(a11*b12 + a12*b22 + a13*b32) + ((a21*b12 + a22*b22 + a23*b32)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31))*(a21*b12 + a22*b22 + a23*b32)]

>> C = A.*D2

C =

[ a11, a21]

[ a12, a22]

[ a13, a23]

>> A^2

Error in MuPAD command: not a square matrix

Матрицу размером 3 на 2 невозможно возвести в квадрат

>> F1^2

ans =

[ (a11*b11 + a12*b21 + a13*b31)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31), (a11*b11 + a12*b21 + a13*b31)*(a11*b12 + a12*b22 + a13*b32) + (a11*b12 + a12*b22 + a13*b32)*(a21*b12 + a22*b22 + a23*b32)]

[ (a11*b11 + a12*b21 + a13*b31)*(a21*b11 + a22*b21 + a23*b31) + (a21*b11 + a22*b21 + a23*b31)*(a21*b12 + a22*b22 + a23*b32), (a21*b12 + a22*b22 + a23*b32)^2 + (a11*b12 + a12*b22 + a13*b32)*(a21*b11 + a22*b21 + a23*b31)]

>> A.^2

ans =

[ a11^2, a12^2, a13^2]

[ a21^2, a22^2, a23^2]

Свойства операций над матрицами.

1. Сложение и вычитание допускается только для матриц одинакового размера.

2. Существует нулевая матрица O такая, что её прибавление к другой матрице A не изменяет последнюю. Все элементы нулевой матрицы равны нулю.

3. Возводить в степень (умножение матрицы на себя) можно только квадратные матрицы.

4. Ассоциативность сложения: A+(B+C)=(A+B)+C.

5. Коммутативность сложения: A+B=B+A.

6. Ассоциативность умножения: A(BC)=(AB)C.

7. Вообще говоря, умножение матриц некоммутативно: AB≠BA.

8. Дистрибутивность умножения относительно сложения:

A(B+C)=AB+AC

(B+C)A=BA+CA.

9. Свойства операции транспонирования матриц:

( A ') '=A

(AB) '=B 'A '

(A+B)'=A '+B '

10. Для квадратных матриц существует единичная матрица (аналог единицы для операции умножения чисел) такая, что умножение любой матрицы на неё не влияет на результат, а именно: EA=AE=A.

Упражнение 7.

1) Проверить на примерах 10 свойств операций над матрицами

2) Ввести матрицы

, B1 = , , , , ,

>> A1 = [1 2 3]

A1 =

1 2 3

>> B1 = [4; 5; 6]

B1 =

4

5

6

>> A = [1 2 3; 4 5 6]

A =

1 2 3

4 5 6

>> B = [ 1 -2 1; -2 3 4]

B =

1 -2 1

-2 3 4

>> c=2

c = 2

>> D=ones(2,3)

D =

1 1 1

1 1 1

>> E=eye(3,3)

E =

1 0 0

0 1 0

0 0 1

3) Выполнить операции (или убедиться, что их выполнить нельзя):

A1+B1, A1*B1, A+B, A.+B, A±c, A+E, A-B, c*A, c.*A, A+c*D, A-c*D, A*B, A.*B, c^3, A’, (A’)’

>> A1 + B1

Matrix dimensions must agree.

>> A1*B1

ans = 32

>> A + B

ans =

2 0 4

2 8 10

>> A .+ B

Error: Unexpected MATLAB operator.

>> A+c

ans =

3 4 5

6 7 8

>> A + E

Matrix dimensions must agree.

>> A-B

ans =

0 4 2

6 2 2

>> A-c

ans =

-1 0 1

2 3 4

>> c*A

ans =

2 4 6

8 10 12

>> c.*A

ans =

2 4 6

8 10 12

>> A +c*D

ans =

3 4 5

6 7 8

>> A-c*D

ans =

-1 0 1

2 3 4

>> A*B

Inner matrix dimensions must agree.

>> A.*B

ans =

1 -4 3

-8 15 24

>> c^3

ans = 8

>> A.*3

ans =

3 6 9

12 15 18

12 15 18

>> A'

ans =

1 4

2 5

3 6

>> (A')'

ans =

1 2 3

4 5 6

Упражнение 8.

Составьте массив w2, содержащий элементы w кроме четвертого. В этом случае удобно использовать  двоеточие и сцепление строк

>> w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8];

>> w2=[w(1:3),w(5:7)]

w2 = 0.1000 2.9000 3.3000 2.6000 7.1000 9.8000