1-й курс / МатЛаб - Алгебра / МП_14_Ермилов_Ярослав_лаб_1_2 (+)
.docxЛабораторная работа №1_2
Работу выполнил: Ермилов Ярослав (МП-14)
Упражнение 1. Функция line (тетрадь+MATLAB)
Построить три отрезка (0,0)______(2,1) , (0,0)______(-1, 2), (-2,-4)______(0,0) .
>> line([0;2],[0;1])
>> line([0;-1],[0;2])
>> line([-2;0],[-4;0])
>> grid on, axis equal
Упражнение 2. Для самостоятельной работы (тетрадь+ MATLAB)
Постройте три отрезка (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) с помощью одной команды line.
>> figure
>> line([0;2],[0;1])
>> line([0;2],[2;0])
>> line([0;3],[2;0])
>> grid on, axis equal
Упражнение 3. Для самостоятельной работы (тетрадь+MATLAB)
Создать графическое окно для четырёх координатных плоскостей. В третьей области построить все три отрезка, в остальных по одному. Прямые: (0,0)____(2,1) , (0,2)_____(2,0) , (0,2)_____(3,0) .
>> subplot(2,2,1)
>> grid on, axis equal
>> line([0;2],[0;1])
>> subplot(2,2,2)
>> grid on, axis equal
>> line([0;2],[2;0])
>> subplot(2,2,3)
>> grid on, axis equal
>> line([0;2],[0;1])
>> line([0;2],[2;0])
>> line([0;3],[2;0])
>> subplot(2,2,4)
>> grid on, axis equal
>> line([0;3],[2;0])
Пример 3. Векторы на плоскости (тетрадь+matlab)
Построим векторы, взяв за их основу отрезки с соответствующими началом и концом:(0,0)______(2,1) , (0,0)______(-1,2), (0,0)______(-2,-4) отметив «концы-стрелочки» в соответствующих точках.
>> figure, grid on, axis equal, hold on
>> line([0,0;2,-1],[0,0;1,2])
>> line([0; -2], [0 -4], 'lineWidth', 4, 'Color', [1 0 0])
>> plot(2,1,'>b','lineWidth',4)
>> plot(-1,2,'^g','lineWidth',4)
>> plot(-2,-4,'vr','lineWidth',4)
Упражнение 4. Для самостоятельной работы. (тетрадь+matlab)
Построить следующие векторы (0,0)____(2,1), (0,2)_____(2,0),(0,2)_____(3,0). Можно пользоваться quiver и line+plot по выбору. Все векторы покрасить в чёрный цвет, установить толщину 3.
>> figure, grid on, axis equal, hold on
>> quiver(0, 0, 2, 1, 1, 'black', 'lineWidth', 3)
>> quiver(0, 2, 2, -2, 1, 'black', 'lineWidth', 3)
>> quiver(0, 2, 3, -2, 1, 'black', 'lineWidth', 3)
Упражнение 5. Векторы в пространстве (тетрадь+MATLAB)
Изобразить векторы-орты координатных осей в пространстве: орты - единичные направляющие векторы
(0, 0, 0) _____________(1, 0, 0)
(0, 0, 0) _____________(0,1, 0)
(0, 0, 0) _____________(0, 0, 1)
>> figure, grid on, axis equal, hold on
>> quiver3(0, 0, 0, 1,0,0, 1, 'red', 'lineWidth', 3)
>> quiver3(0, 0, 0, 0,1,0, 1, 'green', 'lineWidth', 3)
>> quiver3(0, 0, 0, 0,0,1, 1, 'blue', 'lineWidth', 3)
Упражнение 6. Для самостоятельной работы.
a) Изобразить координатные оси двухмерного пространства X, Y толщиной 2, а орты изобразить черным цветом, толщины 4; b) Изобразить координатные оси трёхмерного пространства X, Y, Z толщиной 2, а орты изобразить черным цветом, толщины 4.
Файл XY.m
figure, grid on, axis square, hold on
% создаём оси X,Y
quiver(-5, 0, 10, 0, 1, 'black', 'lineWidth', 2)
quiver(0, -5, 0, 10, 1, 'black', 'lineWidth', 2)
quiver(0, 0, 1, 0, 1, 'black', 'lineWidth', 4)
quiver(0, 0, 0, 1, 1, 'black', 'lineWidth', 4)
Файл XYZ.m
figure, grid on, axis equal, hold on
% создаём оси X,Y,Z
quiver3(0, 0, 0, 5, 0, 0, 1, 'red', 'lineWidth', 2)
quiver3(0, 0, 0, 0, 5, 0, 1, 'green', 'lineWidth', 2)
quiver3(0, 0, 0, 0, 0, 5, 1, 'blue', 'lineWidth', 2)
% создаём орты
quiver3(0, 0, 0, 1, 0, 0, 1, 'red', 'lineWidth', 4)
quiver3(0, 0, 0, 0, 1, 0, 1, 'green', 'lineWidth', 4)
quiver3(0, 0, 0, 0, 0, 1, 1, 'blue', 'lineWidth', 4)
Упражнение 7. Для самостоятельной работы.
Сколько прямых рисует функция line? Изобразить в тетради и в матлаб данные прямые (отрезки), указать координаты точек конца каждой прямой. С помощью команды axis([xmin xmax ymin ymax]) установить оптимальные границы координатных осей, включить отображение координатной сетки, установить одинаковый масштаб по осям.
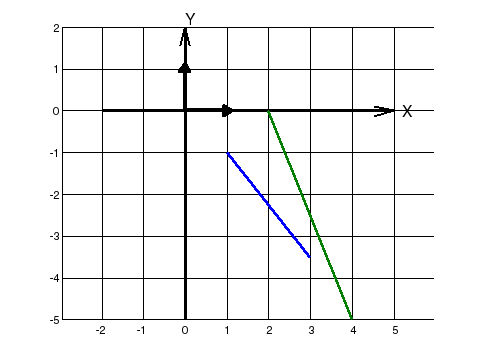
а) line([-1;2],[ 3.5;-5]); б) line([1,2;3,4],[-1,0;-3.5
>> xy
>> line([-1;2],[ 3.5;-5])
Координаты начала = (-1; 3.5), координаты конца = (2; -5)
>> xy
>> line([1,2;3,4],[-1,0;-3.5,-5])
Первый отрезок: Координаты начала = (1; -1), координаты конца = (3; -3.5)
Второй отрезок: Координаты начала = (2; 0), координаты конца = (4; -5)
>> xy
>> line([1,2;3,4],[-1,0;-3.5,-5])
>>
axis([-1
5 -5 1])
Упражнение 8. Правило треугольника.
Изобразить правило треугольника на следующем примере.
Даны три точки с координатами A(-2 0), B(1 2), C(1 -1). Найти векторы АВ, ВС, AC. Убедиться, что АВ+ВС=AC. Изобразить векторы АВ и ВС синим и АС красным, выделить и обозначить вершины (команда text).
Файл lab_1_2_u_8.m
xy
A = [-2, 0]; B = [1, 2]; C = [1, -1];
text(A(1),A(2),'A');
text(B(1),B(2),'B');
text(C(1),C(2),'C');
%line([A(1);B(1)],[A(2);B(2)], [0,0], 'color', 'blue', 'lineWidth', 2);
%line([B(1);C(1)],[B(2);C(2)], [0,0], 'color', 'blue', 'lineWidth', 2);
%line([A(1);C(1)],[A(2);C(2)], [0,0], 'color', 'red', 'lineWidth', 2);
quiver(A(1), A(2), B(1)-A(1), B(2)-A(2), 1, 'blue', 'lineWidth', 2)
quiver(B(1), B(2), C(1)-B(1), C(2)-B(2), 1, 'blue', 'lineWidth', 2)
quiver(A(1), A(2), C(1)-A(1), C(2)-A(2), 1, 'red', 'lineWidth', 2)
Упражнение 9. Правило параллелограмма.
Дан параллелограмм ABCD, известны координаты трёх его точек A(-2 0), B(1 2), C(1 -1). Найти координаты четвертой вершины D (x,y) параллелограмма.
Разбить графическое окно на две области. В первом изобразить параллелограмм с помощью line ABCD, выделить и обозначить вершины (команда text).Найти векторы AB, DC, AD, BC . Доказать, что пары векторов AB и DC, AD и BC коллинеарны, сонаправлены и равны.Во втором графическом окне показать правило параллелограмма: AB+ AD =AC.
Изобразить векторы АВ и AD синим и АС красным,остальные стороны параллелограмма ВС и CD -черным.
Файл lab_1_2_u_9.m
A = [-2, 0]; B = [1, 2]; C = [1, -1];
BA = [A(1)-B(1), A(2)-B(2)];
D = C + BA;
clf; %очистить графическое окно
f_color = 'black'; l_w = 2; f_w = 'bold'; t_d = 0.3;
subplot(1,2,1); xy; axis([-3 2 -4 3]);
text(A(1)-t_d, A(2)+t_d, 0, 'A','Color',f_color, 'FontWeight',f_w);
plot(A(1), A(2), '.', 'Color',f_color);
text(B(1), B(2)+t_d, 0, 'B','Color',f_color, 'FontWeight',f_w);
plot(B(1), B(2), '.', 'Color',f_color);
text(C(1), C(2)-t_d, 0, 'C','Color',f_color, 'FontWeight',f_w);
plot(C(1), C(2), '.', 'Color',f_color);
text(D(1)-t_d, D(2)-t_d, 0, 'D','Color',f_color, 'FontWeight',f_w);
plot(D(1), D(2), '.', 'Color',f_color);
% рисуем линию АB
Point_1 = A; Point_2 = B;
line([Point_1(1),Point_2(1)], [Point_1(2),Point_2(2)], 'Color',f_color, 'lineWidth',l_w)
% рисуем линию BC
Point_1 = B; Point_2 = C;
line([Point_1(1),Point_2(1)], [Point_1(2),Point_2(2)], 'Color',f_color, 'lineWidth',l_w)
% рисуем линию CD
Point_1 = C; Point_2 = D;
line([Point_1(1),Point_2(1)], [Point_1(2),Point_2(2)], 'Color',f_color, 'lineWidth',l_w)
% рисуем линию AD
Point_1 = A; Point_2 = D;
line([Point_1(1),Point_2(1)], [Point_1(2),Point_2(2)], 'Color',f_color, 'lineWidth',l_w)
AB = [B(1)-A(1), B(2)-A(2)]; disp(['AB = {', num2str(AB), '}']);
DC = [C(1)-D(1), C(2)-D(2)]; disp(['DC = {', num2str(DC), '}']);
AD = [D(1)-A(1), D(2)-A(2)]; disp(['AD = {', num2str(AD), '}']);
BC = [C(1)-B(1), C(2)-B(2)]; disp(['BC = {', num2str(BC), '}']);
subplot(1,2,2); xy; axis([-3 2 -4 3]);
text(A(1)-t_d, A(2)+t_d, 0, 'A','Color',f_color, 'FontWeight',f_w);
plot(A(1), A(2), '.', 'Color',f_color);
text(B(1), B(2)+t_d, 0, 'B','Color',f_color, 'FontWeight',f_w);
plot(B(1), B(2), '.', 'Color',f_color);
text(C(1), C(2)-t_d, 0, 'C','Color',f_color, 'FontWeight',f_w);
plot(C(1), C(2), '.', 'Color',f_color);
text(D(1)-t_d, D(2)-t_d, 0, 'D','Color',f_color, 'FontWeight',f_w);
plot(D(1), D(2), '.', 'Color',f_color);
line([B(1),C(1)], [B(2),C(2)], 'LineStyle','--', 'Color',f_color, 'lineWidth',l_w)
line([C(1),D(1)], [C(2),D(2)], 'LineStyle','--', 'Color',f_color, 'lineWidth',l_w)
AC = [C(1)-A(1), C(2)-A(2)];
quiver(A(1), A(2), AB(1), AB(2), 1, 'black', 'Color','b', 'lineWidth',l_w);
quiver(A(1), A(2), AD(1), AD(2), 1, 'black', 'Color','b', 'lineWidth',l_w);
quiver(A(1), A(2), AC(1), AC(2), 1, 'black', 'Color','r', 'lineWidth',l_w);
AB = {3 2}
DC = {3 2}
AD = {0 -3}
BC = {0 -3}
Упражнение 10. Сумма и разность векторов.
Вычислить суму двух векторов a1=(2;3;4), b1=(3;5;2).
Вычислить разность двух векторов a2=(2;3;4), b2=(3;5;2).
Сделать геометрическую интерпретацию в двух областях одного графического окна. Пометить векторы полужирным шрифтом (команда text, {\bf})
Файл lab_1_2_u_10.m
clf; %очистить графическое окно
f_color = 'black'; l_w = 2; f_w = 'bold'; t_d = 0.2;
a1 = [2, 3, 4]; b1 = [3, 5, 2];
a2 = [2, 3, 4]; b2 = [3, 5, 2];
c1 = a1+b1;
c2 = a2-b2;
subplot(1,2,1); xyz % рисуем систему координат;
text(a1(1)-t_d, a1(2)+t_d, a1(3)+t_d, 'a1', 'Color','r', 'FontWeight', 'bold');
text(a1(1) + b1(1), a1(2) + b1(2)+t_d, a1(3) + b1(3), 'b1', 'Color','g', 'FontWeight', 'bold');
text(c1(1), c1(2)-t_d, c1(3)-t_d, 'c1', 'Color','b', 'FontWeight', 'bold');
quiver3(0, 0, 0, a1(1), a1(2), a1(3), 1, 'Color','r', 'lineWidth',l_w);
quiver3(a1(1), a1(2), a1(3), b1(1), b1(2), b1(3), 1, 'Color','g', 'lineWidth',l_w);
quiver3(0, 0, 0, c1(1), c1(2), c1(3), 1, 'Color','b', 'lineWidth',l_w);
subplot(1,2,2); xyz;
text(a2(1)-t_d, a2(2)+t_d, a2(3)+t_d, 'a2', 'Color','r', 'FontWeight', 'bold');
text(a2(1)-b2(1)-t_d, a2(2)-b2(2)+t_d, a2(3)-b2(3)+t_d, 'b2', 'Color','g', 'FontWeight', 'bold');
text(c2(1), c2(2)-t_d, c2(3)-t_d, 'c2', 'Color','b', 'FontWeight', 'bold');
quiver3(0, 0, 0, a2(1), a2(2), a2(3), 1, 'Color','r', 'lineWidth',l_w);
quiver3(a2(1), a2(2), a1(3), -b2(1), -b2(2), -b1(3), 1, 'Color','g', 'lineWidth',l_w);
quiver3(0, 0, 0, c2(1), c2(2), c2(3), 1, 'Color','b', 'lineWidth',l_w);
Упражнение 11. Свойства суммы векторов
Проверить
свойства суммы векторов, используя
векторы
,
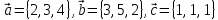сначала непосредственно, затем используя
функцию isequal(…,…).
Сделать геометрическую интерпретацию.
>>a = [2, 3, 4]; b = [3, 5, 2]; c = [1, 1, 1];
>>a + b, b + a
ans = 5 8 6
>> (a + b) + c, a + (b + c)
ans = 6 9 7
>>isequal(a + b, b + a)
ans = 1
>>isequal((a + b) + c, a + (b + c))
ans = 1
a = [2 3 4]; b = [3 5 2]; c = [1 1 1];
Файл lab_1_2_u_10.m
clf; subplot(1,3,1); xyz;
quiver3(0, 0, 0, a(1), a(2), a(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(a(1), a(2), a(3), b(1), b(2), b(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(0, 0, 0, a(1)+b(1), a(2)+b(2), a(3)+b(3), 1, 'Color','r', 'lineWidth',l_w);
subplot(1,3,2); xyz;
quiver3(0, 0, 0, a(1), a(2), a(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(a(1), a(2), a(3), c(1), c(2), c(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(0, 0, 0, a(1)+c(1), a(2)+c(2), a(3)+c(3), 1, 'Color','r', 'lineWidth',l_w);
subplot(1,3,3); xyz;
quiver3(0, 0, 0, b(1), b(2), b(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(b(1), b(2), b(3), c(1), c(2), c(3), 1, 'Color','b', 'lineWidth',l_w);
quiver3(0, 0, 0, b(1)+c(1), b(2)+c(2), b(3)+c(3), 1, 'Color','r', 'lineWidth',l_w);
Упражнение 12. Проверить свойства умножения вектора на число.
Даны
векторы
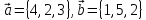и числа
.Использовать
isequal.
>> a = [4, 2, 3]; b = [1, 5, 2]; alpha = 4; beta = 3;
>>isequal(alpha * (a + b ), alpha * a + alpha * b)
ans = 1
>>isequal((alpha + beta) * a , alpha * a + beta * a)
ans = 1
>>isequal(alpha * (beta * a), (alpha * beta) * a)
ans = 1
Упражнение 13. Длина вектора, орт вектора. Пространство.
Длину
вектора
,
вычислить по определению и с помощью
встроенной функции, вычислить орт
.
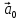Проверить является ли вычисленный
вектор единичным. Изобразить оба вектора.
Упражнение выполнить, создав соответствующий
скрипт.
>> a = [3, 4, 5];
>> a_lenght_1 = sqrt(sum(a.^2))
a_lenght_1 = 7.0711
>> a_lenght_2 = norm(a)
a_lenght_2 = 7.0711
>> a_0 = a / a_lenght_1
A_0 = 0.4243 0.5657 0.7071
>>norm(a_0)
ans = 1
Файл lab_1_2_u_13.m
clf;xyz;
quiver3(0, 0, 0, a(1), a(2), a(3), 1, 'Color','b', 'lineWidth',2);
quiver3(0, 0, 0, a0(1), a0(2), a0(3), 1, 'Color','r', 'lineWidth',2);
text(a(1), a(2), a(3), 'a', 'Color','b', 'FontWeight', 'bold');
text(a0(1), a0(2), a0(3), 'a0', 'Color','r', 'FontWeight', 'bold');
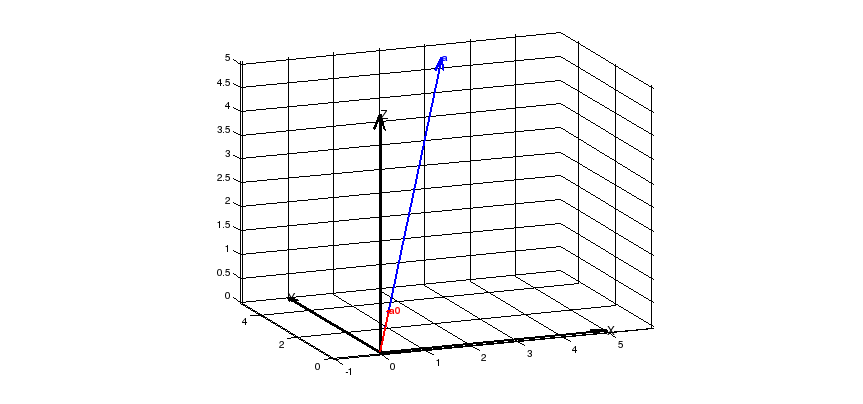
Упражнение 14. Длина вектора, орт вектора. Плоскость.
Длину
вектора
,
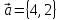вычислить по определению и с помощью
встроенной функции, вычислить орт
.
Проверить является ли вычисленный
вектор единичным. Изобразить оба вектора.
Упражнение выполнить, создав соответствующий
скрипт.
>> a = [4, 2];
>> a_length = sqrt(sum(a.^2)); a_length = norm(a); a_0 = a/a_length;
>> a_length, a_0, norm(a_0)
a_length = 4.4721
a_0 = 0.89443 0.44721
ans = 1
>> quiver(0, 0, a(1), a(2), 1, 'k')
>> quiver(0, 0, a_0(1), a_0(2), 1, 'r', 'lineWidth', 1.5)
Упражнение 15 отсутствует в тексте задания лабораторной работы
Упражнение 16. Направляющие косинусы. Орт вектора. Пространство.
Вычислить
в градусах углы наклона вектора
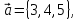к осям координат. Проверить, что сумма
квадратов направляющих косинусов
вектора будет равна единице. Не забудьте
перевести градусы обратно в радианы.
>> a = [3, 4, 5];
>> cos_a = a./norm(a)
cos_a = 0.42426 0.56569 0.70711
>> angles = acos(a./norm(a))*180/pi
angle_a = 64.896 55.55 45
>>sum(cos_a.^2)
ans = 1
Упражнение 17. Направляющие косинусы. Орт вектора. Плоскость.
Вычислить
в градусах углы наклона вектора
к осям координат. Проверить, что сумма
квадратов направляющих косинусов
вектора будет равна единице. Не забудьте
перевести градусы обратно в радианы.
>> a = [2, 4];
>> cos_a = a ./ norm(a)
cos_a = 0.44721 0.89443
>> angle_a = acos(a ./ norm(a)) * 180 / pi
angle_a = 63.435 26.565
>> sum(cos_a .^ 2)
ans = 1
Упражнение 18. Изобразить векторы базиса. Пространство.
Векторы
образуют базис (показать, что векторы
некомпланарны).
Изобразить эти векторы (в виде прямых) с помощью функций line и plot3.
Изобразить
орты
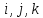черным цветом, толщиной ‘LineWidth’, 4
Вычислить
и изобразить орты векторов
толщиной ‘LineWidth’,4
Упражнение выполнить, создав соответствующий скрипт.
Сразу ввести команды для оформления графика, написать комментарии к ним:
grid on % Рисует координатную сетку
hold on % Позволяет рисовать несколько графиков в одной области
xlabel('X'), ylabel('Y'), zlabel('Z') % Подписывает оси
axis square % Задаёт пропорцинальность графического окна 1:1
axis equal % Задаёт свободную графического окна
disp(['Векторы некомпланарны, так как их смешанное произведение равно ', num2str(det(vertcat(a, b, c))), '.']);
line([0, 0, 0; a(1), b(1), c(1)], [0, 0, 0; a(2), b(2), c(2)], [0, 0, 0; a(3), b(3), c(3)])
line([0, 0, 0; 1, 0, 0], [0, 0, 0; 0, 1, 0], [0, 0, 0; 0, 0, 1], 'lineWidth', 4)
a0 = a/norm(a), b0 = b/norm(b), c0 = c/norm(c)
line([0, 0, 0; a0(1), b0(1), c0(1)], [0, 0, 0; a0(2), b0(2), c0(2)], [0, 0, 0; a0(3), b0(3), c0(3)], 'lineWidth', 4)
Упражнение 19. Изобразить векторы базиса. Плоскость.
Векторы p = {2,-3} и q = {1,2} образуют базис (показать, что векторы неколлинеарны). Найти разложение вектора s = {9,4} по базису p и q: s =mp + nq. Изобразить векторы p, q , mp, nq, s, а также координатные оси Ox и Oy и орты i, j.
Упражнение выполнить, создав соответствующий скрипт
Файл lab_1_2_u_19.m
p = [2, -3]; q = [1, 2]; s = [9, 4];
disp(['px / py = ', num2str(p(1)/p(2)), ', qx / qy = ', num2str(q(1)/q(2))])
disp('Отношения координат не равны, следовательно векторы неколлинеарны')
opr = det(horzcat(p', q'));
opr1 = det(horzcat(s', q'));
opr2 = det(horzcat(p', s'));
m = opr1 / opr;
n = opr2 / opr;
if (n >= 0)
disp(['s = ', num2str(m), 'p+', num2str(n), 'q'])
else
disp(['s = ', num2str(m), 'p', num2str(n), 'q'])
end
mp = m * p;
nq = n * q;
clf; XYZ;
quiver(0, 0, mp(1), mp(2), 1, 'Color', 'm', 'lineWidth', 2)
quiver(0, 0, nq(1), nq(2), 1, 'Color', 'c', 'lineWidth', 2)
quiver(0, 0, p(1), p(2), 1, 'Color', 'r', 'lineWidth', 3)
quiver(0, 0, q(1), q(2), 1, 'Color', 'g', 'lineWidth', 3)
quiver(0, 0, s(1), s(2), 1, 'Color', 'b', 'lineWidth', 2)
text(3, 7, '\bfq', 'Color', 'g');
text(3, -3, '\bfp', 'Color', 'r');
text(6, 3, '\bfs', 'Color', 'b')
Упражнение 20. Разложение вектора по двум неколлинеарным векторам.
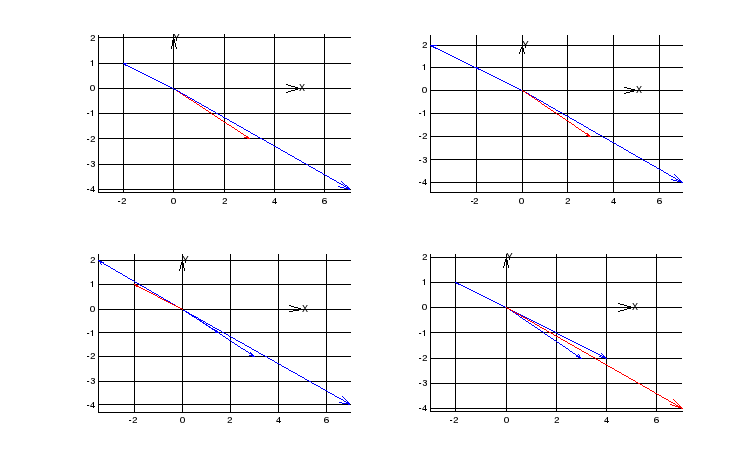
На плоскости даны три вектора a = {3,-2}, b = {-2,1}, c = {7,-4}. Определить разложение каждого из этих трёх векторов, принимая в качестве базиса два других. Графическое окно разбить на четыре области. Во всех окнах изобразить координатные оси Ox и Oy, орты i, j. В первой изобразить три вектора. В оставшихся трёх – геометрическую интерпретацию разложения каждого из этих трёх векторов по двум остальным. Векторы базиса представлять синим цветом, разлагаемый вектор красным.
Файл decomp.m
function [mn] = decomp(p, q, s)
%DECOMP Разложение по векторам
%Раскладывает вектор s по векторам p и q.
opr = det(horzcat(p', q'));
opr1 = det(horzcat(s', q'));
opr2 = det(horzcat(p', s'));
mn = [opr1/opr, opr2/opr];
end
Файл lab_1_2_u_20.m
a = [3, -2]; b = [-2, 1]; c = [7, -4];
deca = decomp(b, c, a);
decb = decomp(a, c, b);
decc = decomp(a, b, c);
clf; subplot(2, 2, 1); XY;
quiver(0, 0, a(1), a(2), 1, 'color', 'r', 'lineWidth', 2)
quiver(0, 0, b(1), b(2), 1, 'color', 'b', 'lineWidth', 2)
quiver(0, 0, c(1), c(2), 1, 'color', 'b', 'lineWidth', 2)
subplot(2, 2, 2); XY;
quiver(0, 0, b(1), b(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, deca(1)*b(1), deca(1)*b(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, c(1), c(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, deca(2)*c(1), deca(2)*c(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, a(1), a(2), 1, 'color', 'red', 'lineWidth', 2)
subplot(2, 2, 3); XY;
quiver(0, 0, a(1), a(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, decb(1)*a(1), decb(1)*a(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, c(1), c(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, decb(2)*c(1), decb(2)*c(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, b(1), b(2), 1, 'color', 'red')
subplot(2, 2, 4); XY;
quiver(0, 0, a(1), a(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, decc(1)*a(1), decc(1)*a(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, b(1), b(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, decc(2)*b(1), decc(2)*b(2), 1, 'color', 'blue', 'lineWidth', 2)
quiver(0, 0, c(1), c(2), 1, 'color', 'red', 'lineWidth', 2)
Упражнение 21. Разложение вектора по трем некомпланарным векторам.
Письменно
и используя графические средства MATLAB
проверить векторы на компланарность
и, если они некомпланарны, разложить
вектор по трем некомпланарным векторам
:
,
считая
ортами прямоугольной декартовой системы
координат, изобразить некомпланарные
векторы
черным
цветом, толщиной ‘LineWidth’, 4, а также
векторы и вектор
.
(
–
коэффициенты разложения – неизвестные
в соответствующей системе уравнений)
Упражнение выполнить, создав соответствующие скрипты.
Файл decomp3.m
function [klm] = decomp3(p, q, r, s)
%DECOMP Разложение по векторам
%Раскладывает вектор s по векторам p, q и r
opr = det(horzcat(p', q', r'));
opr1 = det(horzcat(s', q', r'));
opr2 = det(horzcat(p', s', r'));
opr3 = det(horzcat(p', q', s'));
klm = [opr1/opr, opr2/opr, opr3/opr];
end
Файл lab_1_2_u_21.m
a = [1, 0, 0]; b = [0, 1, 0]; c = [0, 0, 1];
clf;
if (det(vertcat(p, q, r)) == 0) %смешанное произведение
disp('Вектор s нельзя разложить по векторам p, q и r');
else
disp('Вектор s можно разложить по векторам p, q и r');
decs = decomp3(p, q, r, s);
XYZ;
quiver3(0, 0, 0, p(1), p(2), p(3), 1, 'r', 'lineWidth', 2);
text(p(1), p(2), p(3), 'p', 'Color', 'r', 'FontWeight', 'bold');
quiver3(0, 0, 0, q(1), q(2), q(3), 1, 'g', 'lineWidth', 2);
text(q(1), q(2), q(3), 'q', 'Color', 'g', 'FontWeight', 'bold');
quiver3(0, 0, 0, r(1), r(2), r(3), 1, 'b', 'lineWidth', 2);
text(r(1), r(2), r(3), 'r', 'Color', 'b', 'FontWeight', 'bold');
quiver3(0, 0, 0, decs(1)*p(1), decs(1)*p(2), decs(1)*p(3), 1, 'c','lineWidth', 2);
quiver3(0, 0, 0, decs(2)*q(1), decs(2)*q(2), decs(2)*q(3), 1, 'c','lineWidth', 2);
quiver3(0, 0, 0, decs(3)*r(1), decs(3)*r(2), decs(3)*r(3), 1, 'c','lineWidth', 2);
quiver3(0, 0, 0, s(1), s(2), s(3), 1, 'r','lineWidth', 3); text(s(1), s(2), s(3), 's', 'Color', 'r', 'FontWeight', 'bold');
end
>> p = a-b+c; q = b-a-c; r = b-c; s = a+b+c;
>> lab_1_2_u_21
Вектор s нельзя разложить по векторам p, q и r.
>> p = 2*a+b+c; q = a+b; r = b-c;
>> lab_1_2_u_21
Вектор s нельзя разложить по векторам p, q и r.
>> p = a-b+c; q = a+b; r = b-c;
>> lab_1_2_u_21
Вектор s можно разложить по векторам p, q и r.
Упражнение 22. Линейная зависимость четырёх векторов.
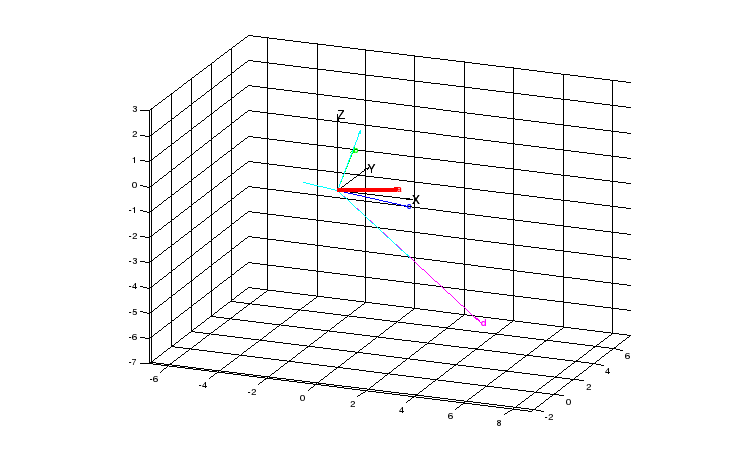
Даны четыре вектора a = {2,1,0}, b = {1,-1,2}, c = {2,2,-1} и d = {3,7,-7}. Определить разложение каждого из этих четырёх векторов, принимая в качестве базиса три остальных. Сделать геометрическую интерпретацию задачи на отдельных четырёх рисунках. Команда figure перед командами, отвечающими за графику, позволяет открывать новое графическое окно. На первом рисунке изобразить координатные оси, орты осей и четыре вектора. На оставшихся трёх – геометрическую интерпретацию разложений. Векторы базиса представлять синим цветом, разлагаемый вектор – красным.
Файл lab_1_2_u_22.m
a = [2, 1, 0]; b = [1, -1, 2]; c = [2, 2, -1]; d = [3, 7, -7];
% По очереди разкомментировать строки:
% p = b; q = c; r = d; s = a;
% p = a; q = c; r = d; s = b;
% p = a; q = b; r = d; s = c;
% p = a; q = b; r = c; s = d;
clf; XYZ;
quiver3(0, 0, 0, a(1), a(2), a(3), 1, 'r', 'lineWidth', 2);
text(a(1), a(2), a(3), 'a', 'Color', 'r', 'FontWeight', 'bold');
quiver3(0, 0, 0, b(1), b(2), b(3), 1, 'g', 'lineWidth', 2)
text(b(1), b(2), b(3), 'b', 'Color', 'g', 'FontWeight', 'bold');
quiver3(0, 0, 0, c(1), c(2), c(3), 1, 'b', 'lineWidth', 2)
text(c(1), c(2), c(3), 'c', 'Color', 'b', 'FontWeight', 'bold');
quiver3(0, 0, 0, d(1), d(2), d(3), 1, 'm', 'lineWidth', 2)
text(d(1), d(2), d(3), 'd', 'Color', 'm', 'FontWeight', 'bold');
if (det(vertcat(p, q, r)) == 0)
disp('Вектор s нельзя разложить по векторам p, q и r.');
else
disp('Вектор s можно разложить по векторам p, q и r');
decs = decomp3(p, q, r, s);
XYZ;
quiver3(0, 0, 0, decs(1)*p(1), decs(1)*p(2), decs(1)*p(3), 1, 'c', 'lineWidth', 2);
quiver3(0, 0, 0, decs(2)*q(1), decs(2)*q(2), decs(2)*q(3), 1, 'c', 'lineWidth', 2);
quiver3(0, 0, 0, decs(3)*r(1), decs(3)*r(2), decs(3)*r(3), 1, 'c', 'lineWidth', 2);
quiver3(0, 0, 0, s(1), s(2), s(3), 1, 'r', 'lineWidth', 3);
end
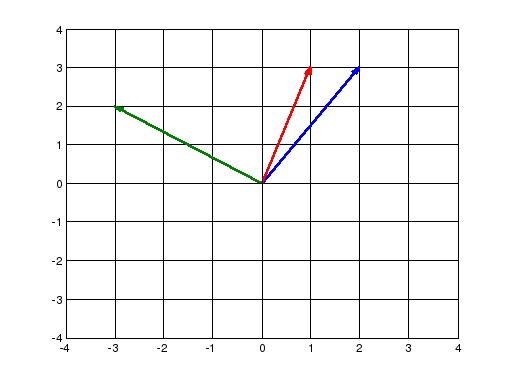
Упражнение 23. Условие ортогональности векторов.
Найти
все векторы, перпендикулярные вектору
.
Изобразить эти векторы.
Файл lab_1_2_u_23.m
a = [2, 3];
b1 = [-a(2), a(1)];
b2 = [a(2), -a(1)];
clf; XY; d = 0.2;
quiver(0, 0, a(1), a(2), 1, 'Color', 'r', 'lineWidth', 3);
quiver(0, 0, b1(1), b1(2), 1, 'Color', 'g', 'lineWidth', 2);
quiver(0, 0, b2(1), b2(2), 1, 'Color', 'b', 'lineWidth', 2);
text( a(1)+d, a(2), 'a', 'Color', 'r', 'FontWeight', 'bold');
text(b1(1)+d, b1(2), 'b1', 'Color', 'g', 'FontWeight', 'bold');
text(b2(1)+d, b2(2), 'b2', 'Color', 'b', 'FontWeight', 'bold');
Упражнение 24.1. Свойства скалярного произведения векторов.
Даны векторы a = {1, -2 ,0}, b = {0, 1, 1} и с = {1, 2, 2}. Используя функцию isequal, проверить свойства 1, 2, 2’, 3, 3’, 4 скалярного произведения векторов.
Скалярное произведение векторов обладает многими свойствами, которыми обладает произведение действительных чисел. Однако, автоматическое (бездумное) перенесение на векторы свойств действительных чисел, которыми векторы не обладают, является ошибочным. В частности, для векторов несправедлив закон ассоциативности (сочетательный закон), т.е. в общем случае
>> a = [1, -2, 0]; b = [0, 1, 1]; c = [1, 2, 2];
>> isequal(dot(a, b), dot(b, a))
ans = 1
>> isequal(dot(a + b,c), dot(a, c) + dot(b, c))
ans = 1
>> isequal(dot(a, b + c), dot(a , b) + dot(a, c))
ans = 1
>> isequal(dot(3 * a, b), 3 * dot(a, b))
ans = 1
>> isequal(dot(a, 3 * b), 3 * dot(a, b))
ans = 1
>> dot(a, a)
ans = 5
>> a = [0, 0];
>> dot(a, a)
ans = 0
Упражнение 24.2. Свойства скалярного произведения векторов.
Даны векторы a = {1, -2 ,0}, b = {0, 1, 1} и с = {1, 2, 2}. Используя функцию isequal, убедиться в невыполнении равенств (2), (3), (4).
(2)
(3)
(4)
>> isequal(dot(dot(a, b), c), dot(a, dot(b, c)))
ans = 0
>> isequal(dot(dot(a, b), b), dot(a, dot(b, b)))
ans = 0
Упражнение 25. Для самостоятельной работы.
Составить
задачи с конкретными векторами,
иллюстрирующие рис.1 и рис.2, а также
показать для первой задачи, что
,
но
;
для второй
,
но
Приведём
ещё примеры. 1) если
векторы, изображённые на рисунке 2, то
1)
,
но
;
2) для векторов на рисунке 3:
,
но
Рис.1. Рис.2.
|
a = [2, 3]; b = [-3, 2]; c = [3, -2]; if dot(a, b)==0 if dot(a, b)*c==0 fprintf('(ab)c=0\n'); if a*dot(b, c)~=0 fprintf('a(bc)~=0'); end end end figure(1); hold on abc = [2, 3; -3, 2; 3, -2]; syms i; for i = 1:3 quiver(0, 0, abc(i, 1), abc(i, 2), 1, 'LineWidth', 2); end grid on line([0 0], [-4 4], 'Color', 'black'); line([-4 4], [0 0], 'Color', 'black'); a = [2, 3]; b = [-3, 2]; c = [1, 3]; if a.*b == a.*c & a.*b == 0 & a.*c == 0 fprintf('ab=ac=0'); if b~=c fprintf('b~=c'); end; end;
figure(1); hold on abc = [2, 3; -3, 2; 1, 3]; syms i; for i = 1:3 quiver(0, 0, abc(i, 1), abc(i, 2), 1, 'LineWidth', 2); end grid on line([0 0], [-4 4], 'Color', 'black'); line([-4 4], [0 0], 'Color', 'black'); |
Упражнение 26.
Вычислить скалярное произведение двух векторов a = {x1, y1, z1}, b = {x2, y2, z2}
>> a = [1, 0]; b = [0, 1]; c = [1, 2]; >> sum(dot(a, b) .* c)
ans = 0
>> isequal(sum(dot(a, b) .* c), sum(a .* dot(b, c)))
ans = 0
>> a = [0, -1]; b =[-1, 0]; c = [1, 0]; >> isequal(b, c)
ans = 0
>> isequal(dot(a, b),dot(a, c))
ans = 1
Упражнение 27.
Выразить
скалярное произведение векторов
,
,
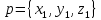т.е.
,
A)
в декартовом базисе
,
,
B)
косоугольном базисе
,
,
. Пользуясь геометри-ческим свойством
скалярного произведения, убедиться,
что векторы a,b,c образуют косоугольный
базис.
C)
в прямоугольном, но не в ортонормированном
базисе
,
,
|
syms x1 x2 y1 y2 z1 z2
p=[x1,y1,z1];q=[x2,y2,z2];
a=[1 0 0]; b=[0 1 0]; c=[0 0 1];
p=[p(1)*a(1) p(2)*b(2) p(3)*c(3)]; q=[q(1)*a(1) q(2)*b(2) q(3)*c(3)];
pq1=sum(p.*q)
a=[1 -2 0]; b=[0 1 1]; c=[0 0 1];
p=[p(1)*a(1) p(2)*b(2) p(3)*c(3)]; q=[q(1)*a(1) q(2)*b(2) q(3)*c(3)];
pq2=sum(p.*q);
a=[3 0 0]; b=[0 4 0]; c=[0 0 5];
p=[p(1)*a(1) p(2)*b(2) p(3)*c(3)]; q=[q(1)*a(1) q(2)*b(2) q(3)*c(3)];
pq3=sum(p.*q);
a = 1 0 0 b = 0 1 0 c = 0 0 1
p =[ x1, y1, z1]; q =[ x2, y2, z2];
pq1 =x1*x2 + y1*y2 + z1*z2;
a = 1 -2 0 b = 0 1 1 c = 0 0 1
p =[ x1, y1, z1]; q =[ x2, y2, z2];
pq2 =x1*x2 + y1*y2 + z1*z2;
a = 3 0 0 b = 0 4 0 c = 0 0 5
p =[ 3*x1, 4*y1, 5*z1]; q =[ 3*x2, 4*y2, 5*z2];
pq3 =9*x1*x2 + 16*y1*y2 + 25*z1*z2; |