Лабораторная работа №3 Ярослав Ермилов (МП-14)

Лабораторная работа №3 Тема

Работу выполнил: Ермилов Ярослав (МП-14)

Упражнение 1. Вычисление определителей III порядка

Создать квадратную матрицу размером 3х3.

Вычислить определитель матрицы B

1)по правилу Саррюса, обращаясь через индексы к элементам массива

2)разложить по первой строке, обращаясь через индексы к элементам массива

3)сделать проверку пунктов 1 и 2, обращаясь к стандартной функции det()

syms a1 a2 a3 b1 b2 b3 c1 c2 c3

B=[a1 b1 c1;

a2 b2 c2;

a3 b3 c3]

detA1=B(1,1)*B(2,2)*B(3,3) + B(1,2)*B(2,3)*B(3,1) + B(1,3)*B(2,1)*B(3,2) - B(1,3)*B(2,2)*B(3,1) - B(1,2)*B(2,1)*B(3,3) - B(1,1)*B(2,3)*B(3,2)

detA2=B(1,1)*(B(2,2)*B(3,3)-B(2,3)*B(3,2))-B(1,2)*(B(2,1)*B(3,3)-B(3,1)*B(2,3))+B(1,3)*(B(2,1)*B(3,2)-B(3,1)*B(2,2))

det(B)

Результат:

B=

[ a1,b1,c1]

[ a2, b2, c2]

[ a3, b3, c3]

detA1 =

a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1

detA2 =

c1*(a2*b3 - a3*b2) - b1*(a2*c3 - a3*c2) + a1*(b2*c3 - b3*c2)

ans =

a1*b2*c3 - a1*b3*c2 - a2*b1*c3 + a2*b3*c1 + a3*b1*c2 - a3*b2*c1

Упражнение 2. Найти векторное произведение векторов

Найти векторное произведение векторов 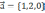ис помощью определителя третьего порядка см формулу (8) и проверить решение стандартной функциейcross(a,b). Вычислить определитель полученной матрицы разложением по первой строке, обращаясь индексами к элементам матрицы. Проверить себя в тетради и стандартными функциямиdet() иcross(a,b)

a = [1, 2, 0]; b = [2, 1, 0];

AxB=[a(2)*b(3)-a(3)*b(2), a(3)*b(1)-a(1)*b(3), a(1)*b(2)-a(2)*b(1)]

cross(a, b)

Результат:

AxB =

0 0 -3

ans=

0 0 -3

Упражнение 3. Вычислить площадь треугольника с помощью векторного произведения

Вычислить площадь треугольника с вершинами иИзобразить плоскость треугольника. Как соотносятся (алгебраически и геометрически)площадь треугольникаи векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.

Решение:

A=[1 3 -1];

B=[2 -1 4];

C=[5 0 3];

AB = B-A;

AC = C-A;

ABxAC = cross(AB,AC);

S = norm(ABxAC)/2

axis3;

quiver3(A(1), A(2), A(3), AB(1), AB(2), AB(3), 1)

quiver3(A(1), A(2), A(3), AC(1), AC(2), AC(3), 1)

quiver3(A(1), A(2), A(3), ABxAC(1), ABxAC(2), ABxAC(3), 1,'g')

quiver3(A(1), A(2), A(3), ABxAC(1)/2, ABxAC(2)/2, ABxAC(3)/2, 1,'r', 'lineWidth', 2)

fill3([A(1), B(1), C(1)], [A(2), B(2), C(2)], [A(3), B(3), C(3)], 'm')

Результат:

S =10.3199

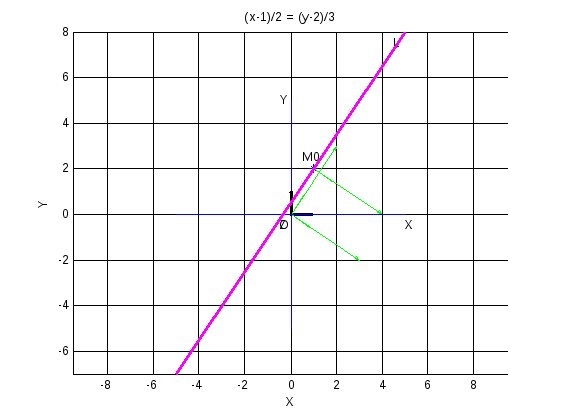
Упражнение 4. Каноническое уравнение прямой.

Пусть прямая Lпроходит через точкупараллельно направляющему вектору.

1. Записать каноническое уравнение прямой (см формулу (3)) и сделать его заголовком графика.

2. Входными параметрами сделать координаты kиlнаправляющего вектораи координатыx₀иy₀ точки.

3. Выразить из канонического уравнения y, как функцию отx.

4. Используя функцию plot(), построить прямуюL, сплошную, фиолетового (m) цвета, толщины 2. Значения абсцисс точек прямой –массив, состоящий из двух точек.

5. Пометить прямую L. Отметить на прямой точку.

6. Провести с помощью функции line( ) оси координат черного цвета. Обозначить начало координат.

7. Построить направляющий вектор и орт вектора, берущими начало

а) в начале координат; б) в точке

8. Найти и построить нормальный вектор и орт вектора, исходящими

а) из начала координат; б) из точки _.

Решение:

k = 2; l = 3; x0 = 1; y0 = 2;

title('(x-1)/2 = (y-2)/3')

x = [-5 : 10 : 5];

y = l*(x-x0)/k+y0;

M0 = [x0, y0];

q = [k, l];

q0 = q/norm(q);

n = [l, -k];

n0 = n/norm(n);

plot(x, y, 'm', 'lineWidth', 2)

plot(M0(1), M0(2), 'b*')

text(4.5, 7.5, 'L'), text(0.5, 2.5, 'M0'),

axis3

quiver(0, 0, q(1), q(2), 1,'color','green');

quiver(x0, y0, q(1), q(2), 1,'color','green');

quiver(0, 0, q0(1), q0(2), 1,'color','green');

quiver(x0, y0, q0(1), q0(2), 1,'color','green');

quiver(0, 0, n(1), n(2), 1,'color','green');

quiver(x0, y0, n(1), n(2), 1,'color','green');

quiver(0, 0, n0(1), n0(2), 1,'color','green');

quiver(x0, y0, n0(1), n0(2), 1,'color','green');