На сортировку / 5 / 77730 / RGR3var77

Министерство образования и науки Республики Казахстан

Некоммерческое акционерное общество

«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»

Кафедра «Тепловые Энергетические Установки»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3

Дисциплина: «Общая теплотехника»

На тему: Теплопроводность и теплопередача

Специальность: Автоматизация и управление – 5В070200

Выполнил: Адаев А. Группа: АУТ-15-5

Вариант: № 77

Проверил: ст.преп. Ем Т.М.

Принята: «__»______2017г.

Алматы, 2017

Содержание

1. Задание……………………………………………………………...3

2. Решение……………………………………………………………..4

3. Список использованной литературы……………………………...7

Работа 3.

(m=7 n=7)

Теплопроводность и теплопередача

Задание 3.1. Определение коэффициента теплопроводности тел градиентным методом.

Рисунок 3.1

Рисунок 3.1

Опытный образец выполнен в виде цилиндрического диска радиуса r =10 мм и толщины δ=1 мм. Он плотно размещен между равномерно нагретым до температуры t₁ =120 + m + 0,2n = 128.4 °С и холодным с температурой t₂ = 20 + 0,1n = 20.2 °С полюсами прибора. Благодаря теплозащитным нагревателям, радиальные потери тепла отсутствуют (см. рисунок 3.1).

Определите значение коэффициента теплопроводности образца (исследуемого материала) λ при стационарном тепловом потоке Q = 23,2 Вт через образец.

Решение:

Решение варианта m = 7 n = 7. Из формулы теплоты теплопроводности (1.1.28)

Q = 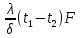, Вт

F = πr²

находим значение коэффициента теплопроводности образца

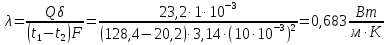
Ответ для варианта m = 7 n = 7, λ = 0,683 Вт/(м К).

Задание 3.2. Теплопередача (1.20 [3]).

Обмуровка печи выполнена из слоя шамотного кирпича с коэффициентом теплопроводности

λ(t) = 0,84(1 + 0,695 10 ³10^-3 t) = λ₀(1 + в t) , Вт/(м К),

Рисунок 3.1

Рисунок 3.2

толщина обмуровки δ = 250мм. Температура газов в печи t_ж1 =1200 —m — n =1186 °С _и температура воздуха в помещении t_ж2 = 30 °С . Коэффициенты теплоотдачи от газов к стенке α₁ =30 + m + 0,5n = 39 Вт/(м² К) и от стенки к окружающему воздуху

α₂ =10 Вт/(м² К) (см. рисунок 3.2).

Определите значения коэффициента теплопередачи k, Вт/(м²К), плотности теплового потока q, Вт/м², и температуры на внешних поверхностях стены t_c1 и t_c2 приближенным методом с точностью более 5%.

Решение варианта m = 7, n = 7. Для определяемых четырех неизвестных составим следующую систему уравнений

q=α₁(t_ж1 – t_с1)

q=(t_c1 – t_c2)

q=α₂(t_c2 – t_ж2)

q=k(t_ж1 – t_ж2)

Для заданной линейной зависимости коэффициента теплопроводности обмуровка печи его среднее интегральное значение равняется

.

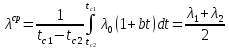Однако λ₁и λ₂, соответствующие определяемым температурам t_c1 и t_c2, являются неизвестными. Следовательно, λ^ср будет пятой неизвестной величиной в системе из четырех уравнений.

Формула коэффициента теплопередачи для плоской стенки, получаемая из первых трех уравнений, не является независимой

Таким образом, рассматриваемая система уравнений является незамкнутой. Поэтому решение задачи рассмотрим методом последовательных приближений.

В качестве первого приближения за среднюю температуру стенки примем среднюю температуру теплоносителей: t_c^cp’ ≈ (1186+30)/2=608 °С и найдем соответствующие значения коэффициентов теплопроводности и теплопередачи стенки, а также плотности теплоты и температуры стенки

λ^ср’=0,84(1+0,695∙10^-3∙608)=1,193 Вт/(м К),

[Вт/(м²К)]

q^’ = k’(t_ж1 – t_ж2) = 2,988(1186 – 30) = 3466 Вт/м²

t_c1‘ = t_ж1 – q'/α₁ = 1186 – 3466/39 = 359 °C

t_c2‘ = t + q'/α₂ = 30 + 3466/10 = 376,608 °C.

Во втором приближении значения средней температуры стенки, коэффициентов теплопроводности и теплопередачи стенки, а также плотности теплоты будут следующими

t_c^cp’’ ≈ (1101,1262+376,608)/2=738,8671 °С

λ^ср’’=0,84(1+0,695∙10^-3∙738,8671)=1,271 Вт/(м К),

[Вт/(м²К)]

q^’’ = k’’(t_ж1 – t_ж2) = 3,102(1190 – 30) = 3598,32 Вт/м²

При этом значении плотности теплоты температуры поверхностей стенки, средняя температура стенки и соответствующее ей значение коэффициента теплопроводности для третьего приближения будут равны

t_c1" = t_ж1 - q''/α₁, =1190 – 3598,98/30 = 1097,74 °С,

t_c2" = t_ж2 + q''/α₂= 30 + 3598,98/10 = 389,832 °С,

t_c^cp"'= (t_с1" + t_c2'')/2 =(1097,74 + 389,832)/2 = 743,79 °C,

λ^{ср’’’}=0,84(1+0,695∙10^-3∙743,79) = 1,274 Вт/(м К),

В третьем приближении среднее значение коэффициента теплопроводности изменилось очень мало, то есть точность его вычисления намного выше, чем заданная

< 5%

В качестве ответов можно принять результаты второго приближения:

t_c1 = t_c1" = 1097,74 °C, t_c2 = t_c2" = 389,832 °С, k = k" = 3,102 Вт/(м² К), q = q" = 3598.32 Вт/м².

Задание 3.3. Определение коэффициента теплопроводности жидкости метод нагретой нити.

Рисунок 3.3

Рисунок 3.3

В приборе для определения коэффициента теплопроводности жидкостей по методу «нагретой нити» (см. рисунок 3.3) в кольцевой зазор 1 между платиновой нитью 3 и кварцевой трубкой 2 залито испытуемое масло 1. Диаметр и длина платиновой нити d₁ = 0,12 и 1 = 90 мм; внутренний и наружный диаметры кварцевой трубки d₂ = 1 и d₃ = 3 мм; коэффициент теплопроводности кварца λ₂ = 1,4 Вт/(м К).

Вычислите коэффициент теплопроводности λ₁ и среднюю температуру t₁^ср масла, если при расходе тепла через кольцевой слой масла Q = 1,8 + 0,1m + 0,1 n = 2,8 Вт, температура платиновой нити t_с1 = 106,9 + m + 0,2n = 115,3 °С и температура внешней поверхности кварцевой трубки t_с3 = 30,6 °С.

Решение варианта m = 7 n = 7. Опытный участок представляет собой двухслойную цилиндрическую стенку, для которой формула теплового потока Q теплопроводностью имеет вид

Отсюда, искомое значение λ₁ с учетом исходных данных определяется следующим образом

Среднюю температуру t₁^Cр трансформаторного масла (как температуру отнесения полученного значения его коэффициента теплопроводности λ₁ = 0,0293 Вт/(м∙К)) найдем приблизительно как среднее значение температур окружающих его стенок

, t_c2= t_с3+=30,6 + = 34,4875°С

t₁^ср= (t_с1 + t_c2)/2 = (115,3 + 34,4875)/2 = 74,89 °С.

Ответ для варианта m = 7 n = 7 λ₁ = 0,0293 Вт/(м К), t₁^ср = 74,89 °С.

Задание 3.4. Критический диаметр.

Рисунок 3.4

Рисунок 3.4

Необходимо теплоизолировать трубопровод с наружным диаметром d₂ = 200 + m + n = 210 мм и температурой наружной поверхности t_с2 = 130 + m + 0,1 n = 138,2 °С, которую можно принять такой же и после наложения изоляции. Пусть температура на внешней поверхности изоляции и линейная плотность тепловые потери не превышают t_c3<30°C и q_i < 200 Вт/м. Коэффициент теплоотдачи от внешней поверхности изоляции к окружающему воздуху α₂ = 10 + m + 0,2 n = 18,4 Вт/(м²К) (см. рисунок 3.4).

Целесообразно ли выбрать в качестве тепловой изоляции материал с коэффициентом теплопроводности λ₂ = 0,05 + 0,1m + 0,1 n = 1,05 Вт/(м К)? Если целесообразно, то какой толщины δ₂ должен быть слой этого теплоизоляционного материала?

Решение варианта m = 7 n = 7. Критический диаметр цилиндрической стенки в предположении α₂ (d₃) = пост определяется следующим образом

Bi = 2; α₂∙d_кр /λ_кр≈2; d_кр^:=2λ₂/α₂ ≈ 2∙1,05/18,4= 0,114м = 114 мм. В данном случае d_кр = 114 мм < d₂ = 210 мм и согласно графическому изображению процесса на рисунке 1.4 применение данного (с λ₂ = 1,05 Вт/(м К)) теплоизоляционного материала (в рассмотренных условиях q_l < q_l^max) приводит к снижению тепловых потерь, следовательно, целесообразно.

При целесообразности использования теплоизоляционного материала, заданного значением коэффициентом теплопроводности, следует определить толщину его слоя δ₂, необходимую для выполнения условий задачи о допустимых значениях плотности тепловых потерь и температуры наружной поверхности изоляции. Для этого используется формула линейной плотности тепловых потоков стационарной теплопроводности

q₁=Q/l = 2πλ₂(t_c2-t_c3)ln(d₂/d₃).

При этом заметим, что для предварительной оценки удобно пользоваться ее более простым приближенным видом, обеспечивающим при d₃/ d₂<2 точность расчета более 4% путем замены логарифма первым слагаемым его разложения в ряд (ln(d₂/d₃) = d₂/(2δ₂))

q₁ |_d3≤2d2≈ 2πλ₂(t_c2 —t_c3)d₂ /(2δ₂).

Согласно приближенной формуле

δ₂ ≈ πλ₂d₂(t_c2 - t_c3)/q₁ = π1,05∙0,21(138,2-30)/200 = 0,375м= 375мм.

Проверка условия приближенного вычисления

d₃^≈ = d₂ + 2δ₂ ≈ 210 + 2∙0,375 = 960 мм; d₃^≈ /d₂ = 231,4/200 = 4,57 > 2 показывает, что она выполняется и можно было бы приближенно принять δ₂ = 375 мм. Однако ошибки приближенных вычислений, как известно, накапливаются и поэтому результаты их могут приняты как оценочные, а реально использоваться, если только удовлетворяют они допустимым их

значениям. В данном случае приближенное (по d₃^≈) расчетное значение плотности тепловых потерь, но определяемое по строгой формуле

q₁^≈расч/q₁^зад = 2πλ₂(t_c2 - t_c3)ln(d₂/d₃^≈)/q₁=2π1,05∙108,2ln(210/960)/200 =1.42

превышает заданное ее значение на 4.2 %, что ниже принятой (по умолчанию) точности рассмотренного приближенного метода, а именно 4 %.

Поэтому принимаем δ₂ = 375 мм как оценочный результат и определяем толщину слоя теплоизоляционного материала по строгой формуле, следующим образом ln(d₃/d₂)=2πλ₂(t_c2-t_c3)/q₁=2π∙1,05∙108.2/200=3.57, d₃/d₂ = 1,17, d₃= 1,17d₂ = 1,17∙210 = 245,7 мм; δ₂=(d₃-d₂)/2 = (245-210)/2 = 18 мм. (1.18)

Ответ для варианта m = 7 n = 7 применение данного варианта теплового изоляционного материала целесообразно, и достаточная его толщина равняется 18 мм.

Задание 1.5. Определение истинной температуры среды.

Температура воздуха в резервуаре измеряется ртутным термометром, который помещен в гильзу (стальную трубку), заполненную маслом (с. рисунок 1.5). Термометр показывает температуру конца гильзы t₁= 84 + 0,2m + 0,1n = 85,8 °С.

Как велика ошибка измерения за счет отвода тепла по гильзе путем теплопроводности, если температура у основания гильзы t_o=40°C, длина гильзы l = 120 + m + 0,1n = 128,2 мм, толщина гильзы δ = 1,5 ™, коэффициент теплопроводности материала гильзы λ = 55,8 – m = 47,8 Вт/(м К) и коэффициент теплоотдачи от воздуха к гильзе α = 23,3 + 0,1m = 23,5 Вт/(м²К).

Рисунок 4.5

Рисунок 4.5

Решение варианта m = 8 n = 2. Для решения воспользуемся приближенной формулой для стержня конечной длины

Где m = – параметр дифференциального уравнения теплопроводности стержня, м^-1;

u = πd- периметр гильзы;

f = πdδ – сечение гильзы, м².

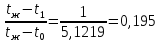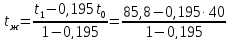Отсюда u/f ≈ 1/δ, m = , ml = 18,104 • 0,128 = 2,317, ch (2,317 ,0) = 5,1219, следовательно, , =96,89 °C.

Ответ для варианта m = 7 n = 7: Истинная температура воздуха t_ж = 96,89°С, ошибка измерений t_ж – t₁ = 100 - 84 = 11,09 °С.

Список литературы

1. Техническая термодинамика. Расчет термодинамических процессов и теплосиловых циклов. Программа курса, методические указания к выполнению расчетно-графических работ для студентов всех форм обучения специальности 050717 - Теплоэнергетика. - Алматы: АИЭС. 2008.- 34с.

2. Кириллин В. А., Сычев В. В., Шейндлин А. Е. Техническая термодинамика.-М.: Энергоатомиздат, 1983.-416с.

3. Ривкин С. Л., Александров А. А. Термодинамические свойства воды и водяного пара.-М.: Энергоатомиздат, 1984.-80с.

4. Сборник задач по технической термодинамике: Уч. пособие / Т.Н. Андрианова и др.-М.: Ичд, МЭИ, 2000.-356с