На сортировку / 5 / 77730 / TOE_Muhtarov_RGR_3

Noncommercial Joint Stock Company

ALMATY UNIVERSITY OF POWER ENGINEERING & TELECOMMUNICATIONS

Department of Theoretical Bases of Electrical Engineering

CALCULATION GRAPHICAL WORK № 3

on the “Analysis of Electrical Circuits and Electric Field” discipline

Calculation of electrostatic and magnetostatic fields

on the 5B071800 – “Electrical power engineering” baccalaureate specialty

Done by: Muhtarov A.N. student of the EPEe-15-11 group (Student’s Surname & Initials) (Academic group code)

Checked by: associate professor Baimaganov A.S

(Teacher’s academic degree, academic rank, Surname & Initials)

___________ _________________ “_____” “_____________” 201__ y.

(Score) (Teacher’s signature) (Date)

Content

1. Introduction…………………………………………………………………..…3

   1. Assignment……….………………………………………………………...3

2. Calculation procedure…………………………………………………………...4

3. Conclusion…………………………………………………………………..…11

4. List of references……………………,,……………………………………......12

3.1 Assignment

The assignment includes two problems on the themes:

- Calculation of electrostatic field;

- Calculation of magnetic field of direct current.

The task numbers that have to be solved and the options of initial data for the calculation are presented in tables 3.1... 3.3.

Problem 3.4.

Spherical earth electrode with radius R is located deeply in the ground with a specific conductivity γ1 at a distance d from the interface plane between two media with specific conductivities γ1 and γ2, see figure 3.4. The direct current I is supplied to the earth electrode The influence of the ground surface can be neglected.

It is necessary:

- to calculate the spreading voltage Us;

- to calculate the electric field strength at the points A and D with coordinates RA and RD.

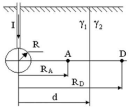
Figure 3.4

Problem 3.6.

The two-wire line consists of long cylindrical wires of circular cross section. The radii of wires are identical and are R. The wires arranged in parallel to each other at a distance d. Current is I, which flows through the line, the environment is air, see the figure 3.6.

It is necessary:

- for option c): to determine the external inductance Lext per unit of line length.

Figure 3.6

2.Calculation procedure

odd	ВМЧ
Problems	3.4. 3.6c
ε1	-
ε2	-
τ1, nC/m	-
τ2, nC/m	-
Xk, m	-
d,m	0,75
R,mm	4
h1,m	0.30
y1,mS/m	80
I1,A	27
Rd,m	1
y2,mS/m	40
μw	250
Xn,m	0.35
b,m	0.65
h2,m	0,95
U,V	920
Rgr,m	0.10
Ra,m	0.42
Rc,m	0.47
I,A	75
Yn,m	0.65
w	700
a,m	0.25

Problem 3.4.

When calculating the electric field in an inhomogeneous conductive medium, the image method is applied.

We calculate the electric field of a spherical earth electrode with a radius R₃=0,05m. The earthing device is deep in the ground with the specific conductivity ₁=610^-2 Smm^-1 at a distance d = 0,9 m from the interface of two media with specific conductivities ₁ and ₂. Specific conductivity ₂=310^-2 Smm^-1. A current I = 50 A is applied to the earth electrode (figure 3.4)

Figure 3.4

Calculation of the electric field in a medium with specific conductivity ₁

The electric field in the medium with ₁, where the earth electrode is located, is calculated from the set current I and the dummy current .

In this case, we consider a homogeneous medium with specific conductivity ₁

(Fig. 8.2.3). The effect of the ground surface is neglected.

We apply the principle of superposition. We calculate the voltage Us using the formula:

Calculation of the electric field strength

We calculate the electric field strength at point A, R_A = 0,42 m.

We apply the principle of superposition. Electric field strength

where - is the vector of the electric current intensity I

- is the vector of the electric current intensity I₁.

Since ₁₂, the currents I and I₁ have the same signs. The directions of the vectors , and are shown in Figure 8.2.3.

The module of the tension vector is calculated by the formula:

Calculation of the electric field in a medium with specific conductivity ₂.

The electric field in a medium with specific conductivity ₂is calculated from the dummy current (Figure 8.2.4).

Calculation of the electric field strength

The electric field strength at the point D (R_D=1,2 m) is calculated by the formula:

Problem 3.6.

The two-wire line consists of long cylindrical wires of circular cross section. The radii of wires are identical and are R= 410^-3 m. The wires arranged in parallel to each other at a distance d=0.75 m. Current is I=75 A, which flows through the line, the environment is air, see the figure 3.6.

C) Calculation of the external inductance of a two-wire line.

Figure 3.6.1

The external magnetic flux linked to the line in a section of length is calculated by the formula:

Magnetic induction is found by the principle of superposition

where - is the magnetic induction of a single wire 1;

         - magnetic induction of a single wire 2.

Magnetic induction , directed perpendicular to the plane passing through the wires, from us.

From here

If you select the direction of traversal of the path along path 1234, vectors and are directed in the same direction.

The external flow will be:

The external flux coupling is _out=Ф_out, since the magnetic flux Ф_out is coupled to the current I once.

From here

The external inductance per unit length of the line ()

Conclusion

In this calculation graphical work I calculated the potential difference U between wires and the vector of magnetic field strength at point N. When calculating electrostatic fields in inhomogeneous media, when electric charges are located near the interface between two media with different electrical properties, the image method is applied.

List of references

1. John Bird. Electrical Circuit Theory and Technology. – Third edition, Lina-cre House, Jordan Hill, Oxford OX2 8DP, UK: 2007. – 679 p.

2. Electromagnetic Field Theory. Bo Thide and Mattias Waldenvik. – Uppsala, Sweden, 2012. – 298 p.

3. Richard Fitzpatrick. Maxwell’s Equations and the Principles of Electromag-netism. – Infinity Science Press LLC: Hingham, 2008. – 438 p.

4. Additional references

5. Бессонов Л. А. ТОЭ. Электромагнитное поле. – М.: Гардарики, 2003. – 317 с.: ил.

6. Денисенко В. И., Зуслина Е. Х. ТОЭ. Учебное пособие. – Алматы:

   1. АИЭС, 2000. – 83 с.

Almaty,2017