Введение

Надежность электроснабжения потребителей электроэнергии во многом зависит от механической прочности всех конструктивных элементов установок для канализации электроэнергии (линий электропередачи, подстанций, токопроводов и т. д.). В свою очередь провода и тросы воздушных линий, токоведущие шины токопроводов и подстанций, их технические характеристики и действующие на них в процессе эксплуатации нагрузки в значительной степени предопределяют конструктивные решения, принимаемые при проектировании и сооружении упомянутых выше сетевых устройств. Целью механического расчета является в конечном счете определение напряжений в материале проводов, тросов и шин при заданных сочетаниях расчетных условий для различных режимов работы (нормальный режим — при необорванных проводах и тросах, аварийный режим — при обрыве части проводов и тросов при расчете ВЛ или режим короткого замыкания при расчете токопроводов и ошиновок открытых подстанций).

Полученные в результате расчета значения механических напряжений в материале токоведущих частей и тросов используются в дальнейшем при решении отдельных частных задач (например, при определении величин стрел провеса проводов и тросов, а также расстояний от проводов до земли или сооружений, для расчета мест установки фиксирующих устройств — распорок на токопроводах, при проектировании защиты от вибрации и т. п.). Объем механического расчета определяется главным образом его целевым назначением, т. е. конечными результативными данными, которые являются необходимыми в каждом конкретном случае для проектирования отдельных конструктивных элементов установки. В отечественной технической литературе, посвященной вопросам проектирования механической части ВЛ и подстанций [Л. 10, 14], достаточно полно изложена теория расчета проводов и тросов, положенная в основу приведенных здесь материалов, цель которых — в элементарной форме и сокращенном объеме дать практические рекомендации по отдельным наиболее часто встречающимся в практике элементам механического расчета проводов, тросов и токоведущих шин.

Провода и тросы воздушных линий в процессе эксплуатации периодически подвергаются воздействию внешних нагрузок от давления ветра (горизонтальные нагрузки), образующегося на них гололеда (вертикальные нагрузки) и одновременно от обоих (суммарные нагрузки). Эти нагрузки во многом определяют величины механических напряжений, возникающих в материале проводов и тросов, и поэтому механический расчет производится с учетом подобных дополнительных нагрузок. При этом во всех случаях учитывается также собственный вес провода или троса.

1 Расчетная часть

Под аварийным режимом воздушной линии понимают работу при полностью или частично оборванных проводах и тросах.

     Основная задача механического расчета проводов в аварийном режиме заключается в определении величин тяжения и провеса провода в пролетах, смежных с аварийным.

 Изменение тяжения провода в результате смежения его точки подвеса называется редукцией, а установившиеся новое тяжение – редуцированным.

Изменение тяжения провода, или редукция, зависит в основном от конструкции опоры, длины гирлянды, нагрузки и длины пролета до обрыва провода.

Длина гирлянды оказывает большое влияние  на редуцированное тяжение. Чем длиннее гирлянда, тем больше ее отклонение и тем меньше редуцированное тяжение провода. Длина пролета также влияет на редуцированное тяжение: чем больше пролет, тем доля его изменения вследствие отклонения гирлянды.

     Целью расчета аварийного режима воздушной линии является определение  редуцированного тяжения. Оно представляет нагрузку на промежуточную опору в аварийном режиме. По редуцированному тяжению определяют стрелы провеса и производят проверку габарита провода до земли и до пересекаемых инженерных сооружений.

    В задаче необходимо определить тяжение, отклонение гирлянды и стрелу провеса провода после его обрыва во втором пролете от анкерной опоры.

    До обрыва поддерживающая гирлянда висит вертикально, и провод занимает положение с каким- то начальным тяжением Н_о. После обрыва провода гирлянда отклоняется на угол φ, пролет уменьшается на Δℓ = i, а тяжение уменьшается до Н< Н_о. Для решения задачи следует применить графический способ с построением кривых тяжения провода и отклонения гирлянды.

Уменьшение пролета на Δℓ определяется по выражению:

∆ℓ=(2.1)

 

Эта формула выражает зависимость перемещения точки подвеса от тяжения.

 

                    Отклонение гирлянды определяется  

 

                                           i =(2.2)

             При  жестком креплении провода  Δℓ = I, поэтому из уравнений (2.1) и (2.2) получаем одно уравнение с одним неизвестным – тяжением H.

 

∆ℓ= 

 Аналитическое решение этого уравнения затруднительно, так как искомое тяжение H  входит в правую часть уравнения под знаком корня. Поэтому обычно применяется графический способ решения с построением кривой по уравнению (2.1) и кривой по уравнению (2.2). Точка пересечения кривых дает решение уравнения: абсцисса этой точки определяет отклонение гирлянды I, а ордината  - искомое редуцированное тяжение  H. 

АС-240/56;

Н₀=2375 даН

Е=8,9∙10³даН/мм²

G_г =68 даН

λ =1,4 м

ℓ = 170 м

1.1 Расчет точек для кривой длины изменения пролета

где - длина изменения пролета.

Рассчитываем вес провода

Вычисляем коэффициенты уравнений

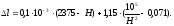
Н0, даН	Н, даН	2375-Н	0,1∙10-3(2375-Н)				ℓ
2375	2375	0	0	0,018	0	0	0
2375	2000	375	0,0375	0,025	0,007	0,008	0,046
2375	1500	875	0,0875	0,044	0,026	0,03	0,12
2375	1000	1375	0,1375	0,1	0,082	0,0943	0,232
2375	500	1875	0,1875	0,4	0,382	0,44	0,63
2375	200	2175	0,02	2,5	2,48	2,8	2,82