На сортировку / 5 / 77724 / лаба 3 твимс Алиш

Содержание

1-7 Задание…………………………………………………………………….3-12

Заключение……………………………………………………………………….13

Список литературы……………………………………………………………..14

Задание 1. В урне 80 шаров одинакового размера и веса, среди них 15 белых, остальные чёрные. Шары тщательно перемешаны. Найти:

1) относительную частоту белых шаров в урне;

2) вероятность того, что все 7 шаров, взятых наугад из урны, будут белыми;

3) вероятность того, что среди 7 шаров, взятых наугад из урны, будет 5 белых.

Решение:

1)P*(A)=15/80=3/16

_2)P(A)=

3)P(A)=

Задание 2. В сборный цех поступило 1000 деталей из трёх цехов: 270 деталей из первого цеха, 340 - из второго, остальные из третьего. В первом, втором и третьем цехах производится соответственно 9, 5 и 4 процентов нестандартных деталей. Наугад выбрана одна деталь: 1) найти вероятность того, что она нестандартная; 2) выбранная деталь оказалась нестандартной. Найти вероятность того, что она сделана в 3 цехе .

Решение:

1) Вероятность события Алматы находится по формуле полной вероятности:

P(A)=P(B₁)P(A/B₁)+P(B₂)P(A/B₂)+P(B₃)P(A/B₃), где P(A/B_i) – условные вероятнсти того, что выбранная наугад деталь из i-го цеха. По условию задачи имеем: P(B₁)=270/1000=0,27; P(B₂)=340/1000=0,34; P(B₃)=390/1000=0,39; P(A/B₁)=0,09; P(A/B₂)=0,05; P(A/B₃)=0,04. Поэтому P(A)=0,27 0,09+0,340,05+0,390,04=0,0569;

2) По формуле Байеса имеем :

Задание 3. Проводится n испытаний, в каждом из которых вероятность появления некоторого события равна 0,6. Найти вероятность того, что событие появится:

1) ровно k₂ раз (событие А);

2) менее k₁ раз (событие B);

3) более k₂ раз (событие C);

4) хотя бы один раз (событие D);

5) от k₁ до k₂ раз (событие E);

а) n=7 k₁=3, k₂ =6; б) n=100, k₁=50, k₂ =70

Выполнение задания:

а) n=7 k₁=3, k₂ =6

Итак, результаты:

1. событие А = 0.131

2. событие В = 0,096

3. событие С = 0,028

4. событие D = 0.998

5. событие E = 0.876

_б)

1. Итак, по таблице:

_{P(A)=P100(70)}

_{2) P(B)=P100}(k<50)=P(0,50)=

_{3) P(C)=P(k>70)=P(70,100)=}

4) P(D)=1-P(D)=1-P₁₀₀(0)=1

т.к

а P₁₀₀(0)=0

_{5)P(E)=P(50,70)=}

Задание 4. Дискретная случайная величина F(x) задана рядом распределения

Найти:

1) её функцию распределения F(x), построить график F(x);

2) математическое ожидание, дисперсию, среднее квадратическое

отклонение, моду;

3) вероятность попадания Х в интервал (1;6)

Решение:

1)Вычисление функции распределения и построение её графика:

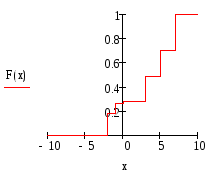
2) вычисление числовых характеристик:

А) Математическое ожидание: т.к

Б) Дисперсия: т.к

а

В) Среднее квадратическое отклонение: т.к

Г) Мода М₀=7;

3) вероятность попадания Х в интервал (1;6):

P(1;6) = F(6) - F(1)= 0.7 – 0.28=0.42

Задание 5. Непрерывная случайная величина Х задана плотностью распределения f(x). Найти:

1) её функцию распределения F(x);

2) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;

3) вероятность попадания Х в интервал (1;2).

Построить графики F(x) и f(x).

Решение:

1) Функция распределения

2) M(X)=

D(X)=

(X) =

Для определения моды находим максимум функции f(x)=(x+2)/6 на отрезке [0;2] . Т.к функция монотонна, то максимум достигается на конце отрезка , т.е f(2)=2/3.

Итак, М₀ =2/3.

Медиана. Так как P(X  M_e )  0,5 P(  X  M_e )  (0  X  M_e) = = (M_e²+4M_e)/12=0.5

получим два корня, из которых подходит один: M_e = 1,1625 – медиана.

3) Вероятность попадания Х в интервал (1;2) равна

Задание 6. Аппаратура состоит из 2000 элементов. Вероятность отказа одного элемента за время t не зависит от состояния других элементов и равна 0,001. Найти:

1) закон распределения числа отказавших элементов;

2) вероятность отказа не менее 4 элементов за время t.

Решение:

₁₎

Искомый закон распределения:

2)

Итак ,вероятность отказа не менее трёх элементов равна: 0,053

Задание 7.Случайная ошибка измерения (случайная величина Х ) подчинена нормальному закону распределения с параметрами а =10 и  =2. Найти:

1) плотность распределения f(x);

2) функцию распределения F(x);

3) математическое ожидание, дисперсию;

4) вероятность попадания в интервал (8;17);

5) вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине  =2.

Построить графики f(x) и F(x).

Решение:

Заключение

В этой лабораторной работе были изучены примеры применения Mathcad к решению задач теории вероятностей: непосредственный подсчёт вероятностей, формулы полной вероятности, Байеса, формулы Бернулли, Пуассона, локальная и интегральная теоремы Лапласа, дискретные и непрерывные случайные величины, некоторые основные законы распределения случайных величин, формулы для функции распределения для дискретной случайной величины и закона Пуассона, Бернулли, локальной и интегральная теоремы Лапласа.

Список литературы

Астраханцева Л.Н., Жуматаева С. А., Нурпеисов С. А., Теория вероятности и математическая статистика. Методические указания по выполнению лабораторных работ для студентов,2014.

14