
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ НИУ «МЭИ»
Кафедра инженерной теплофизики
Лабораторная работа № 5
Решение уравнения нестационарной обобщённой диффузии
Группа Тф-10-14
Вариант 3
Студенты Виноградов М.
Москва 2017
1 Задание
Имеется плоский канал стабилизированным ламинарном течении, с равномерной распределённой температуры по сечению. После определённого участка, начали равномерно подогревать сверху и снизу, одинаковыми тепловыми потоками. Считаем, что свойства жидкости от температуры не зависят, определить длину термического участка.
Дискретный аналог
Неявная схема



Явная схема


Схема Кранка-Николсона


Программа для неявной схемы



Дано

Определим как меняется среднемассовая температура по сечению
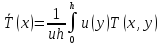
В случаи неявной схемы она выглядит следующим образом

Определим КТО от стенки, который определить можно

Температуру стенки,
можем считать равной при
 ,
для этого потребуется взять сетку по
(у) достаточно большую, чтобы выполнить
это условия
,
для этого потребуется взять сетку по
(у) достаточно большую, чтобы выполнить
это условия

Определим число Нуссельта


4) По этому графику видно, что данная программа хорошо сходиться с теоритическим точками, возможно расхождение связанно из-за недостаточно величины сетки, по (х).



Как видно, при увеличение сетки он приближается, к теоритическому значению
5) Пользуясь с правилом положительных коэффициентов дискретного аналога уравнение переноса было получено, что отношение характерных длин для явной схемы выглядит следующим образом
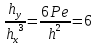
6) Для явной схемы определим при каком (n), у нас нарушается устойчивость алгоритма







|
|
|
|
|
n |
|
30 |
33,333 |
5 |
0.2 |
3.226 |
|
150 |
6,666 |
10 |
0.1 |
2.95 |
|
1025 |
0,9756 |
20 |
0.05 |
2.91 |
Как видно по этой таблице, (n) получается заниженная
7) Расхождение с опытными точками объясняется тем что было выбрано малая сетка. Расхождение между неявной и Кранка-Никольсона тем что 2 схема менее устойчивая чем неявная, что и сделала отклониться зависимость дальше чем точное значение.

Задача 2
Имеется некий компонентный стенка из 2 разных материалов, толщена одного слоя Δ1 другого Δ2, который повторяется 5 раз. Система первоначальное время находилась в стационарном состоянии полностью теплоизолированной при температуре (T0), с левой стороны стенки подвели источник тепла, который равномерно нагревал стенку тепловым потоком (q). Через некоторое время (Δt), источник убирают и теплоизолируют эту стенку. Определить, как меняется среднее температура стенки, со временем.

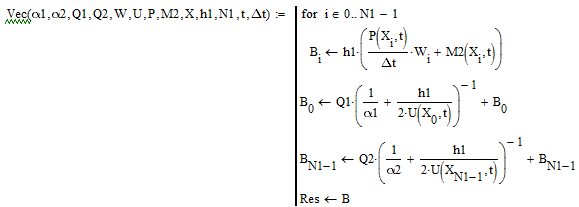

Дано (1)


Вывод средней температуры в стенки

Теоритический вывод


(4)


5) Особых изменений не наблюдается при изменение шага по времени, при изменение контрольных объёмов в каждом слою проявляется в том, что при уменьшении их в неконсервативная схеме начинается более сильный потеря энергии возникают, в консервативной наоборот как будто возникает дополнительный источник тепла.
6) Расхождение между консервативной схемы и неконсервативной в том что, значение коэффициента теплопроводности в случаи неконсервативной схемы у нас меняется коэффициент теплопроводности, из-за чего возникает переопределение тепла. В консервативной схеме мы используем постоянную эффективную теплопроводность из-за чего переопределение эффект перераспределение тепла отсутствует




