
Комплект материалов для подготовки к контрольным мероприятиям для групп мп-21,22,23,24,25 (1-й поток) и для групп мп-26, 27, 28, 29 (2-й поток) Модуль 2
1. Подготовка к контрольной работе № 3
Контрольная работа № 3 состоит из 2-х частей: часть 1 включает 6 заданий, часть 2 – два задания. Правильное решение каждого задания части 1 оценивается 1 баллом. Правильное решение каждого задания части 2 оценивается ориентировочно 2 баллами. Максимальное количество баллов, которое можно получить за контрольную работу № 3, составляет 10 баллов. Начисленные баллы учитываются в рамках накопительной балльной системы.
Контрольная работа № 3 рассчитана на 1 час 20 минут. Структура контрольной работы показана в табл. 1, примерные варианты КР № 3 приведены в таблице 2.
|
Таблица 1 | |
|
№ |
Описание задания |
|
|
Часть 1 |
|
1 |
Неориентированный граф задан множеством вершин и ребер: а) построить диаграмму; б) указать какой-либо путь, не являющийся цепью; какую-либо цепь, не являющуюся простой цепью; цикл, не являющийся простым; простой цикл (в каждом варианте что-нибудь одно). |
|
2 |
Для данного графа найти: а) цикломатическое число; б) хроматическое число. |
|
3 |
а) Построить неориентированный граф по матрице смежности (инцидентности); б) Найти матрицу смежности или инцидентности графа. |
|
4 |
а) Написать код дерева (в одних вариантах бинарный, в других – из натуральных чисел); б) Построить дерево по коду (в одних вариантах по бинарному, в других – из натуральных чисел). |
|
5 |
Ориентированный граф задан множеством вершин и ребер: а) построить диаграмму; б) определить, является ли граф связным, сильно связным. |
|
6 |
а) Построить ориентированный граф по матрице смежности (инцидентности); б) Найти матрицу смежности или инцидентности орграфа. |
|
7 |
Задача из перечня задач повышенной сложности главы 3 учебного пособия Олейник Т.А. Основы дискретной математики: теория и практика. М.:МИЭТ, 2010. |
|
8 |
Задача из перечня задач повышенной сложности главы 3 учебного пособия Олейник Т.А. Основы дискретной математики: теория и практика. М.: МИЭТ, 2010. |
Таблица 2
|
|
Примерный вариант 1 КР №3 |
|
|
Часть 1 |
|
1. |
Пусть
а)
Построить диаграмму графа
б)
Указать на графе
|
|
2. |
Для
графа
а) цикломатическое число; б) хроматическое число, указать соответствующую раскраску. |
|
3. |
а) Построить граф по матрице инцидентности
б) Для графа из п. а) выписать матрицу смежности. |
|
4. |
а) Нарисовать какое-нибудь дерево с 8-ю ребрами, занумеровать его вершины и построить его код из натуральных чисел. б) Построить дерево по коду (0000010101011111). |
|
5. |
Пусть
а)
Построить диаграмму графа
б)
Является ли граф
|
|
6. |
а)
Построить граф по матрице смежности
б) Выписать матрицу инцидентности графа из п. а). |
|
7 |
Доказать, что в связном графе любые две простые цепи максимальной длины имеют по крайней мере одну общую вершину. |
|
8 |
Доказать,
что граф
|
|
|
Примерный вариант 2 КР №3 |
|
|
Часть 1 |
|
1. |
Пусть
а)
Построить диаграмму графа
б)
Указать на графе
|
|
2. |
Для
графа
а) цикломатическое число; б) хроматическое число. |
|
3. |
а) Построить граф по матрице инцидентности
б) Для графа из п.а) выписать матрицу смежности. |
|
4. |
а) Нарисовать какое-нибудь корневое дерево с 9-ю ребрами и построить его бинарный код. б) Построить дерево по коду[2 2 5 5 5 9 5 9]. |
|
5. |
Пусть
а)
Построить диаграмму графа
б)
Является ли граф
|
|
6. |
а)
Построить граф по матрице инцидентности
б) Выписать матрицу смежности графа из п. а). |
|
Часть 2 | |
|
7. |
Показать,
что граф с
|
|
8. |
Используя
теорему Кирхгофа, показать, что число
остовов
в
полном
графе
|
Задания 2-й части контрольной работы №3 формулируются на основе и с использованием банка задач, приведенного в учебном пособии Олейник Т.А. «Основы дискретной математики: теория и практика. М.:МИЭТ, 2010»: Л.1. § 3.1 - § 3.8, задачи повышенной сложности 3.1 – 3.42.
Для подготовки к выполнению части 2 контрольной работы № 3 рекомендуется прорешать задачи из этого списка.

 - граф с вершинами
- граф с вершинами и ребрами
и ребрами ,
,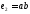 ,
, ,
,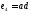 ,
, ,
,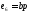 ,
, .
. .
. какой-либо путь, не являющийся цепью,
и простой цикл.
какой-либо путь, не являющийся цепью,
и простой цикл. (задание
1) найти:
(задание
1) найти: .
. - ориентированный граф с вершинами
- ориентированный граф с вершинами и дугами
и дугами
 ,
, ,
, ,
, ,
, .
. .
. связным? сильно связным?
связным? сильно связным? .
.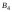 непланарен.
непланарен. - граф с вершинами
- граф с вершинами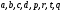 и множеством ребер
и множеством ребер ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.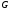 .
. какую-либо цепь, не являющуюся простой
цепью, и простой цикл.
какую-либо цепь, не являющуюся простой
цепью, и простой цикл. (задание
1) найти:
(задание
1) найти: .
. - ориентированный граф с вершинами
- ориентированный граф с вершинами и дугами
и дугами
 ,
, ,
, ,
, ,
, .
. .
. связным? сильно связным?
связным? сильно связным? .
. вершинами и двумя компонентами
связности имеет не более
вершинами и двумя компонентами
связности имеет не более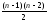 ребер.
ребер. спомеченными
вершинами равно
спомеченными
вершинами равно
 .
.