МП - 3 семестр / Diskretka / -order-52364-StudWork №52364 от 06.01.13 (графы)

Вариант №39.

Задание. Найти число остовов графа, нарисовать их и найти остов минимального веса.

Решение:

Теорема (Кирхгоф). Число остовов в связном графе G порядка n≥2 равно алгебраическому дополнению любого элемента матрицы Кирхгофа K(G) графа G.

Матрицей Кирхгофа графа G называется матрица:

Алгебраические дополнения всех элементов матрицы Кир­хгофа равны между собой.

Составим матрицу Кирхгофа для данного графа:

Отсюда алгебраическое дополнение, например, элемента равно 21.

Значит, и число остовов данного графа равно 21.

Изобразим их:

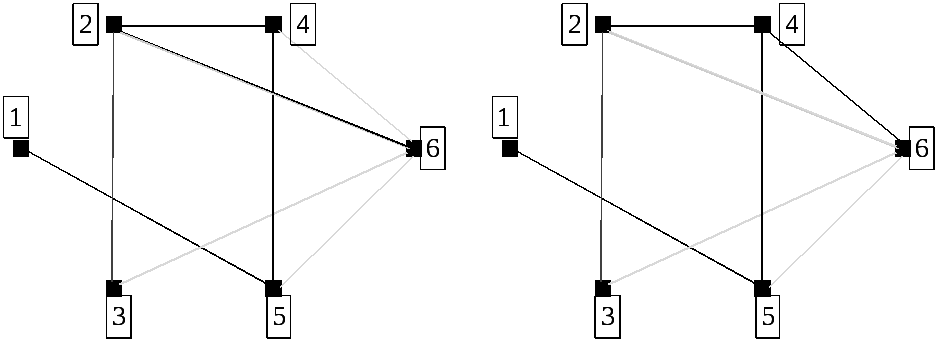
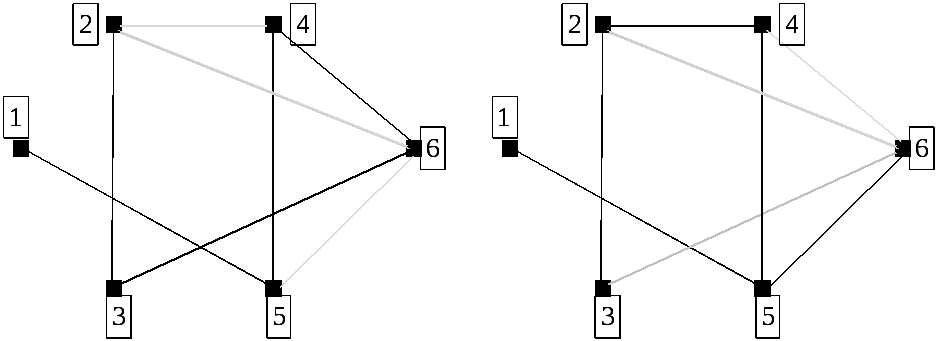
Найдем остов минимального веса с помощью алгоритма Краскала.

Шаг 1. Установка начальных значений.

Введем матрицу длин ребер C:

Шаг 2. Выберем ребро минимальной длины.

Минимальная длина ребра равна 390. Это ребро (2,3). Построим граф G₂, состоящий из данного ребра и инцидентных ему вершин 2 и 3. Положим i = 2.

Шаг 3. Так как n = 6, то i ≠ n, поэтому переходим к шагу 4.

Шаг 4. Строим граф G₃, добавляя к графу G₂ новое ребро минимальной длины, выбранное среди всех ребер графа G, каждое из которых инцидентно одной из вершин 2, 3 и одновременно инцидентно какой-нибудь вершине графа G, не содержащейся в G₂, т.е. одной из вершин 1, 4, 5, 6. Таким образом, нужно выбрать ребро минимальной длины из ребер (2,4), (2,6), (3,6). Такое ребро имеет длину 468 и оно одно: (2,4). Вместе с этим ребром включаем в G₃ вершину 4, не содержащуюся в G₂. Полагаем i = 3 и переходим к шагу 3.

Шаг 3. Так как i ≠ n, поэтому переходим к шагу 4.

Шаг 4. Строим граф G₄, добавляя к графу G₃ новое ребро минимальной длины из ребер (3,6), (2,6), (4,5), (4,6). Такое ребро имеет длину 624 и оно одно: (2,6). Вместе с этим ребром включаем в G₄ вершину 6, не содержащуюся в G₃. Полагаем i = 4 и переходим к шагу 3.

Шаг 3. Так как i ≠ n, поэтому переходим к шагу 4.

Шаг 4. Строим граф G₅, добавляя к графу G₄ новое ребро минимальной длины из ребер (4,5), (6,5). Такое ребро имеет длину 702 и оно одно: (4,5). Вместе с этим ребром включаем в G₅ вершину 5, не содержащуюся в G₄. Полагаем i = 5 и переходим к шагу 3.

Шаг 3. Так как i ≠ n, поэтому переходим к шагу 4.

Шаг 4. Строим граф G₆. Осталась только одна вершина в графе G, не включенная в G₆ – это вершина 1. Так как инцидентное ей ребро только одно, то добавим его в граф G₆ вместе в вершиной 1. Полагаем i = 6 и переходим к шагу 3.

Шаг 3. Так как i = n, то граф G₆ – искомое минимальное остовное дерево.

Суммарная длина ребер равна 390 + 468 + 624 + 702 + 468 = 2652.

Процесс построения минимального остовного дерева:

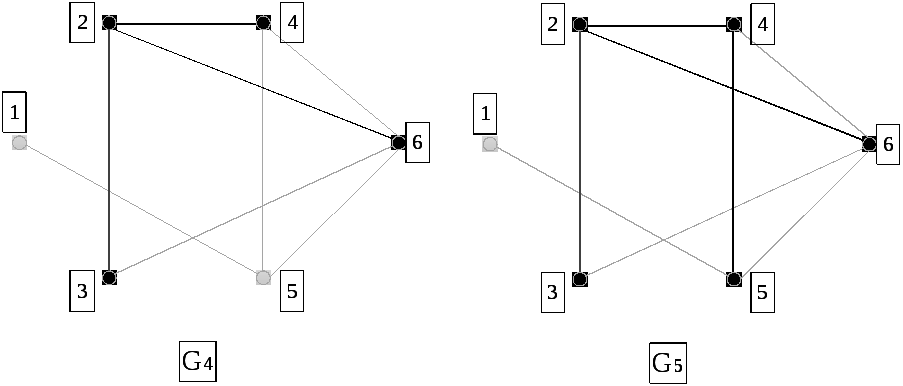
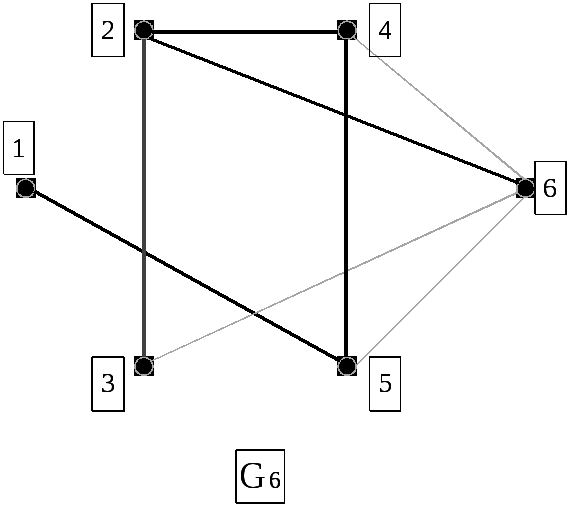
5) Задание. Найти нижнюю и верхнюю оценки числа внутренней устойчивости неориентированного графа, заданного своей матрицей смежности m:

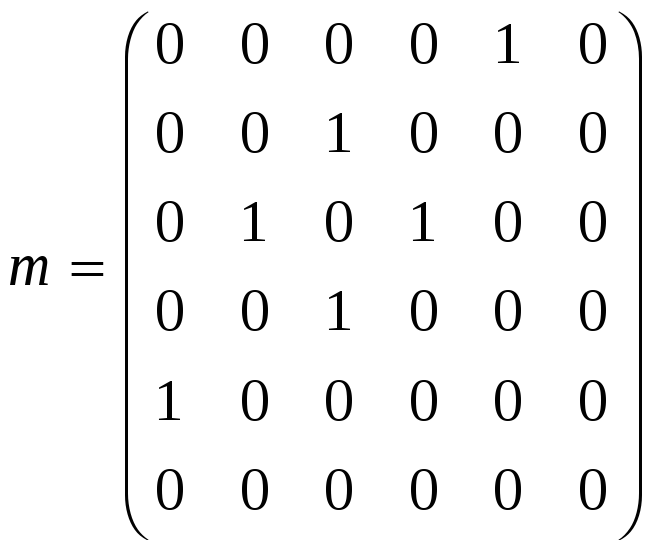
Решение:

Для всех единиц выписываются парные дизъюнкции:

Приведем выражение к ДНФ:

Число внутренней устойчивости равно 2.

Задание. Построить матрицу смежности, найти её 3-ю степень и число ориентированных маршрутов длины 3 из вершины 1 в вершину 4.

Решение:

Матрица смежности A = (a_ij) – это квадратная матрица порядка n, где n – число вершин, у которой:

Матрица смежности данного графа:

Найдем её третью степень:

Длиной маршрута называется количество ребер в нем.

Для определения маршрутов, состоящих из k ребер (дуг), необходимо возвести в k-ю степень матрицу смежности вершин A. Тогда элемент матрицы даст количество маршрутов длины k (состоящих из k ребер) из вершины в вершину .

Таким образом, число ориентированных маршрутов длины 3 из вершины 1 в вершину 4 равно элементу = 4.

Задание. Построить матрицу инциденций и найти число остовов.

Матрицей инцидентности B = (b_ij) ориентированного графа называется прямоугольная матрица (n×m), где n – число вершин, m – число ребер, у которой:

Матрица инциденций данного графа:

Составим матрицу Кирхгофа для данного графа:

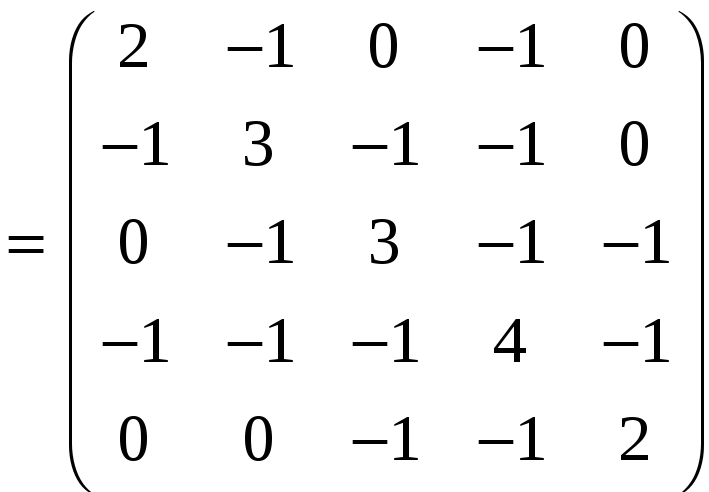
Отсюда алгебраическое дополнение, например, элемента равно 0.

Значит, у данного графа остовов нет.