Добавил:

nyan Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

Схемотехника

Файл:

0350_Minimizatsiya_FAL_s_pomoschyu_kart_Karno__Studentam

.pdf

Скачиваний:

Добавлен:

24.11.2017

Размер:

421.96 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Минимизация функций алгебры логики

Якунин А.Н.

МИЭТ

МИНИМИЗАЦИЯ ФАЛ

Минимизация ФАЛ – это процедура нахождения оптимального представления ФАЛ.

Критерии оптимизации:

количество вентилей, вес;

габариты

энергопотребление;

стоимость;

быстродействие;

надёжность;

перечень допустимых элементов;

коэффициент разветвления …

МИНИМИЗАЦИЯ ФАЛ

Методы минимизация ФАЛ:

расчётный метод (метод непосредственных преобразований);

расчётно табличный метод (КвайнаМак Класки);

метод Петрика;

карты Карно;

метод гиперкубов (геометрический метод);

метод факторизации;

метод функциональной декомпозиции …

КАРТА КАРНО

Карта Карно является специальной компактнойформой таблицы истинности, расположенной в виде матрицы.

В таблице истинности 2n строк => в карте Карно 2n клеток.

Каждая клетка соответствует одному набору.

Каждая из n переменных встречается в половине наборов без инверсии, а в другой – с инверсией.

Линии снаружи указывают, что в соответствующих им

половинах клеток указанная переменная встречается без инверсии. x1

x2	6	7	5	4
2		3	1	0

			x0

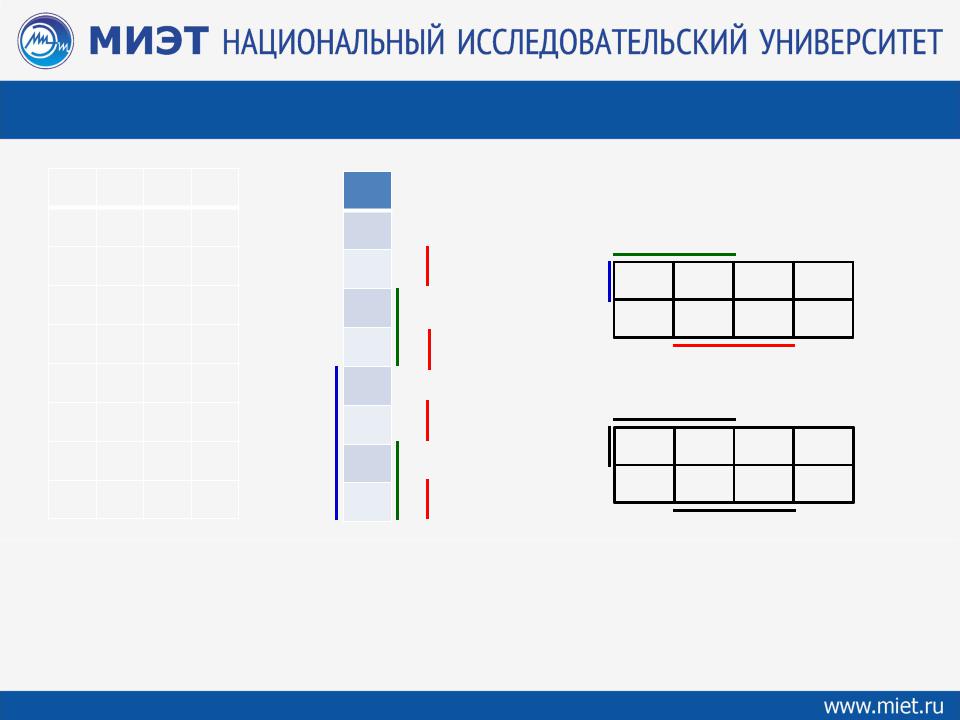
ЭТАЛОННАЯ КАРТА КАРНО

N	x2	x1	x0
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

	N
	0		x0			x1
	1			x2	110	111	101	100
	2
		x1			010	011	001	000
	3		x0
							x0
	4
						x1
	5		x0
x2				x2	6	7	5	4
	6	x1
					2	3	1	0
	7		x0
							x0

Можно «протянуть» линию вдоль карты. Те клетки, которую пересечёт линия, там переменная встречается без инверсии.

КАРТА КАРНО

Можно произвольно поменять местами переменные x2, x1, x0, но тогда обязательно поменять расположение наборов.

Соседние клетки карты Карно всегда содержат соседние наборы.

		x1							x0			x2
x2	6	7	5	4	x2	4	6	7	5	2	6	4	0
x2	6	7	5	4	x2	4	6	7	5	2	6	4	0
2		3	1	0	0		2	3	1	3	7	5	1	x0

			x0					x1			x1

Не смотря на то, что карта Карно изображается на плоскости, с точки зрения обеспечения соседства клеток, карты нужно считать трёхмерными.

Так, при n = 3 – цилиндр, при n = 4 – тор.

СОСЕДНИЕ НАБОРЫ

Соседние наборы – это те, которые отличаются значением одной логической переменной. Например:

0 (000) и 1 (001) – соседние; 1 (001) и 3 (011) – соседние; 3 (011) и 7 (111) – соседние.

1 (001) и 2 (010) – не являются соседними! Соседние наборы всегда располагаются в

геометрически соседних клетках карты Карно.

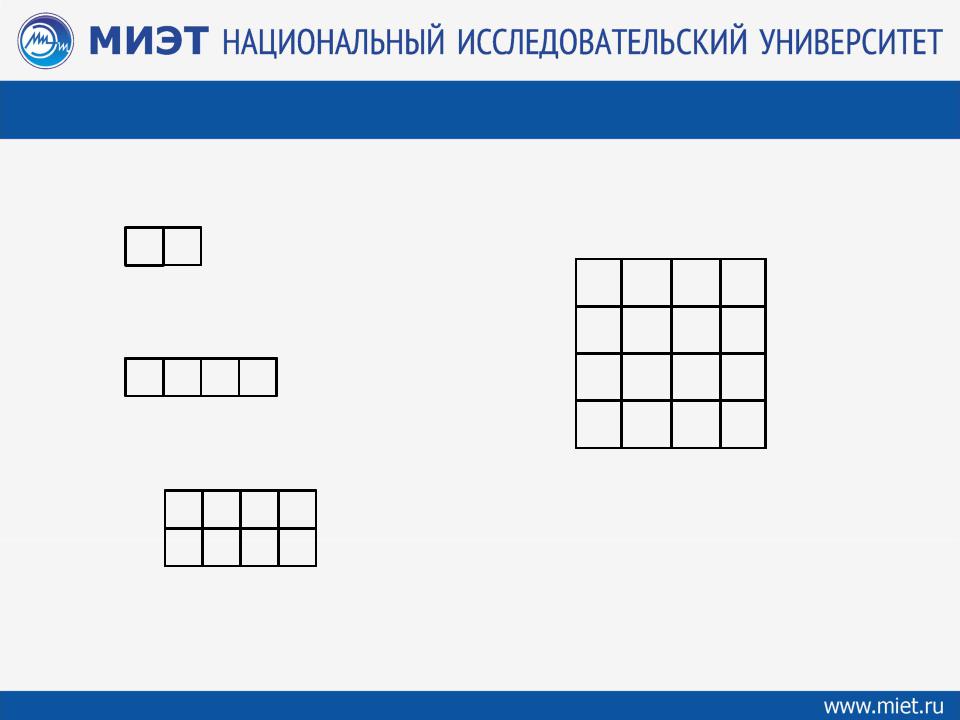
ОБЩЕПРИНЯТЫЕ ЭТАЛОННЫЕ КАРТЫ КАРНО

n = 1:

n = 2:

n = 3:

1	0					x1
1	0						11	9	8
					10
x0				x3	10
x0
x1					14		15	13	12
x1				n = 4:	14		15	13	12	x2
2	3	1	0	n = 4:			7	5	4	x2
2	3	1	0	6			7	5	4

		x0		2			3	1	0

		x1
x2		x1			x0
	6	7	5	4


2		3	1	0

			x0

ОБЩЕПРИНЯТЫЕ ЭТАЛОННЫЕ КАРТЫ КАРНО

n = 5:

			x2			x1
						x1
		21	23	22	18	19	17	16
x4	20	21	23	22	18	19	17	16
	28	29	31	30	26	27	25	24	x3



12		13	15	14	10	11	9	8
12		13	15	14	10	11	9	8
4		5	7	6	2	3	1	0
4		5	7	6	2	3	1	0


			x0				x0

ОБЩЕПРИНЯТЫЕ ЭТАЛОННЫЕ КАРТЫ КАРНО

n = 6:

			x2				x1
							x1
	36		37	39	38		35	33	32
	36		37	39	38	34	35	33	32
x5	44		45	47	46	42	43	41	40	x3
	44		45	47	46	42	43	41	40
		60	61	63	62	58	59	57	56


		52	53	55	54	50	51	49	48
		52	53	55	54	50	51	49	48


x4		20	21	23	22	18	19	17	16
		28	29	31	30	26	27	25	24	x3



12			13	15	14	10	11	9	8
12			13	15	14	10	11	9	8
4			5	7	6	2	3	1	0
4			5	7	6	2	3	1	0


				x0				x0

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в папке Учебники и методички

#
24.11.2017293.53 Кб700200_Logicheskie_ventili__Studentam.pdf
#
24.11.2017350.6 Кб710300_Formyi_predstavleniya_FAL__Studentam.pdf
#
24.11.2017421.96 Кб710350_Minimizatsiya_FAL_s_pomoschyu_kart_Karno__Studentam.pdf
#
24.11.2017773.53 Кб264BOROBEV.pdf
#
24.11.20171.86 Mб307BOROBEV2.pdf
#
24.11.20171.55 Mб95LAB01PR.pdf
#
24.11.2017558.97 Кб68lab_m2_vt_vt_aloiscevm_niy06.pdf
#
24.11.2017441.05 Кб102lab_m3_vt_vt_aloiscevm_niy06.pdf

	N
	0		x0			x1
	1			x2	110	111	101	100
	2
		x1			010	011	001	000
	3		x0
							x0
	4
						x1
	5		x0
x2				x2	6	7	5	4
	6	x1
					2	3	1	0
	7		x0
							x0

			x2			x1
						x1
		21	23	22	18	19	17	16
x4	20	21	23	22	18	19	17	16
	28	29	31	30	26	27	25	24	x3



12		13	15	14	10	11	9	8
12		13	15	14	10	11	9	8
4		5	7	6	2	3	1	0
4		5	7	6	2	3	1	0


			x0				x0

			x2				x1
							x1
	36		37	39	38		35	33	32
	36		37	39	38	34	35	33	32
x5	44		45	47	46	42	43	41	40	x3
	44		45	47	46	42	43	41	40
		60	61	63	62	58	59	57	56


		52	53	55	54	50	51	49	48
		52	53	55	54	50	51	49	48


x4		20	21	23	22	18	19	17	16
		28	29	31	30	26	27	25	24	x3



12			13	15	14	10	11	9	8
12			13	15	14	10	11	9	8
4			5	7	6	2	3	1	0
4			5	7	6	2	3	1	0


				x0				x0

	N
	0		x0			x1
	1			x2	110	111	101	100
	2
		x1			010	011	001	000
	3		x0
							x0
	4
						x1
	5		x0
x2				x2	6	7	5	4
	6	x1
					2	3	1	0
	7		x0
							x0

			x2			x1
						x1
		21	23	22	18	19	17	16
x4	20	21	23	22	18	19	17	16
	28	29	31	30	26	27	25	24	x3



12		13	15	14	10	11	9	8
12		13	15	14	10	11	9	8
4		5	7	6	2	3	1	0
4		5	7	6	2	3	1	0


			x0				x0

			x2				x1
							x1
	36		37	39	38		35	33	32
	36		37	39	38	34	35	33	32
x5	44		45	47	46	42	43	41	40	x3
	44		45	47	46	42	43	41	40
		60	61	63	62	58	59	57	56


		52	53	55	54	50	51	49	48
		52	53	55	54	50	51	49	48


x4		20	21	23	22	18	19	17	16
		28	29	31	30	26	27	25	24	x3



12			13	15	14	10	11	9	8
12			13	15	14	10	11	9	8
4			5	7	6	2	3	1	0
4			5	7	6	2	3	1	0


				x0				x0

	N
	0		x0			x1
	1			x2	110	111	101	100
	2
		x1			010	011	001	000
	3		x0
							x0
	4
						x1
	5		x0
x2				x2	6	7	5	4
	6	x1
					2	3	1	0
	7		x0
							x0

			x2			x1
						x1
		21	23	22	18	19	17	16
x4	20	21	23	22	18	19	17	16
	28	29	31	30	26	27	25	24	x3



12		13	15	14	10	11	9	8
12		13	15	14	10	11	9	8
4		5	7	6	2	3	1	0
4		5	7	6	2	3	1	0


			x0				x0

			x2				x1
							x1
	36		37	39	38		35	33	32
	36		37	39	38	34	35	33	32
x5	44		45	47	46	42	43	41	40	x3
	44		45	47	46	42	43	41	40
		60	61	63	62	58	59	57	56


		52	53	55	54	50	51	49	48
		52	53	55	54	50	51	49	48


x4		20	21	23	22	18	19	17	16
		28	29	31	30	26	27	25	24	x3



12			13	15	14	10	11	9	8
12			13	15	14	10	11	9	8
4			5	7	6	2	3	1	0
4			5	7	6	2	3	1	0


				x0				x0