
Имитационное моделирование_УГАТУ
.docx-
Содержание работы
Система на рис. 1 задана в виде логической схемы соединения подсистем. При этом считают, что подсистема работоспособна, если ее выход связан с входом. Другими словами, если связь отсутствует (существует обрыв), подсистема неработоспособна. Это относится и к системе в целом. Подобная схема замещения эквивалентна электрической цепи: если по ней протекает ток, система работоспособна, если цепь оборвана – система отказала.
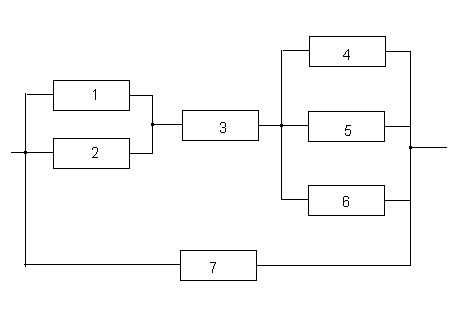
Рисунок 1. Логическая схема работы системы
Для каждой подсистемы задан закон распределения времени, в течение которого подсистема работоспособна.
-
Экспоненциальное распределение
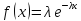 с параметром =1/20 1/час;
с параметром =1/20 1/час;
-
Симметричное треугольное распределение
 ,
заданное на отрезке с=2 часа, d=18 часов;
одно случайное число, распределенное
по этому закону, может быть получено
как сумма двух случайных чисел с
равномерным законом на интервале [c/2,
d/2];
,
заданное на отрезке с=2 часа, d=18 часов;
одно случайное число, распределенное
по этому закону, может быть получено
как сумма двух случайных чисел с
равномерным законом на интервале [c/2,
d/2]; -
Нормальное распределение
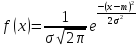 с параметрами m=16 часов,
σ=2 часа;
с параметрами m=16 часов,
σ=2 часа; -
Равномерное распределение
 с параметрами a=2 часа,
b=14 часов;
с параметрами a=2 часа,
b=14 часов; -
Нормальное (усечено-нормальное)
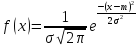 распределение с параметрами m=12 часов,
σ=2 часа;
распределение с параметрами m=12 часов,
σ=2 часа; -
Экспоненциальное распределение
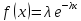 с параметром =1/10 1/час;
с параметром =1/10 1/час; -
Равномерное распределение
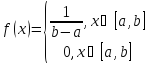 с параметрами a=1 час, b=29 часов.
с параметрами a=1 час, b=29 часов.
Требуется по этим данным построить имитационную модель функционирования системы и с ее помощью определить следующие характеристики системы как целого:
-
закон распределения времени безотказной работы всей системы
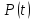 :
:-
Смоделировать
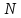 реализаций случайного процесса
функционирования системы для различных
значений
реализаций случайного процесса
функционирования системы для различных
значений
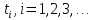 и получить таким образом ряд значений
и получить таким образом ряд значений
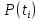 ;
; -
Полученный ряд сгладить непрерывной функцией по методу наименьших квадратов;
-
-
среднее время безотказной работы системы;
-
вероятность того, что система не откажет в течение заданного промежутка времени
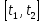 (значения границ выбрать самостоятельно);
(значения границ выбрать самостоятельно); -
построить графики законов распределения времени безотказной работы подсистем (для этого модель не требуется), сравнить с результатом п. 1) и провести сравнительный анализ безотказности системы и ее подсистем.
-
Теоретический материал
Имитационное моделирование
Имитационное моделирование – воспроизведение на ЭВМ (имитация) процесса функционирования исследуемой системы с соблюдением логической и временной последовательности реальных событий.
При имитационном моделировании тип и структура моделирующего алгоритма обусловлены не типом уравнений и не применяемым для их решения численным методом, а имитацией реальных явлений с сохранением их логической структуры, временной последовательности и состава информации о состояниях процесса.
Рассмотрим, как проводится имитационное моделирование. Для этого возьмем в качестве примера систему из трех подсистем (блоков), которая изображена на рис.2.
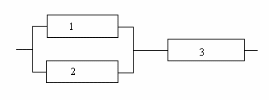
Рисунок 2. Пример системы из трех блоков
Система функционирует
нормально, если исправен хотя бы один
из блоков 1 и 2, а также исправен блок 3.
Функции распределения времени безотказной
работы блоков
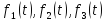 известны. Требуется найти вероятность
безотказной работы системы в момент
времени
известны. Требуется найти вероятность
безотказной работы системы в момент
времени
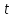 .
.
Решение «в лоб»
Если время работы системы
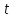 ,
а
,
а
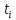 – время безотказной работы элемента с
номером
– время безотказной работы элемента с
номером
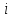 ,
то:
,
то:
-
событие
 означает исправную работу элемента за
время
означает исправную работу элемента за
время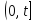 ;
; -
событие
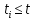 означает отказ элемента к времени
означает отказ элемента к времени
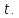
Заметим, что
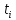 - случайная величина, распределенная
по закону
- случайная величина, распределенная
по закону
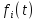 ,
который известен по условию.
,
который известен по условию.
Моделирование случайного
события «исправная работа
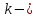 го элемента за время
го элемента за время
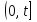 заключается:
заключается:
-
в получении случайного числа
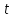 ,
распределенного по закону
,
распределенного по закону
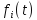 ;
; -
в проверке истинности логического выражения
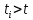 .
Если оно истинно, то -й элемент исправен,
если ложно – он отказал.
.
Если оно истинно, то -й элемент исправен,
если ложно – он отказал.
Для моделирования фиксированного
момента времени
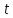 используют следующий алгоритм:
используют следующий алгоритм:
-
Положить
 .
В данном случае
.
В данном случае
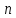 - счетчик числа реализаций случайного
процесса, а
- счетчик числа реализаций случайного
процесса, а
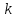 - счетчик числа «успехов».
- счетчик числа «успехов». -
Получить три случайных числа
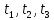 ,
распределенных соответственно по
законам
,
распределенных соответственно по
законам
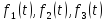 .
. -
Проверить истинность логического выражения:
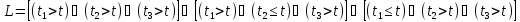
Если
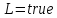 ,
то положить
,
то положить
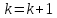 и перейти к шагу 4, иначе просто перейти
к шагу 4.
и перейти к шагу 4, иначе просто перейти
к шагу 4.
-
Положить
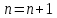 .
. -
Если
 ,
то перейти к шагу 2, иначе вычислить и
вывести
,
то перейти к шагу 2, иначе вычислить и
вывести
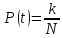 .
Здесь
.
Здесь
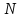 - число реализаций случайного процесса,
от которого зависят точность и
достоверность результатов.
- число реализаций случайного процесса,
от которого зависят точность и
достоверность результатов. -
Стоп.
Значение
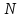 необходимо задавать по соображениям
обеспечения точности о достоверности
статистической оценки искомой величины
необходимо задавать по соображениям
обеспечения точности о достоверности
статистической оценки искомой величины
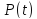 .
Данное значение рекомендуется задать
в промежутке
.
Данное значение рекомендуется задать
в промежутке
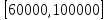 .
.
Данное решение можно упростить, изменив способ получения случайных чисел. Для этого воспользуемся методом обратных функций.
Метод обратных функций
Существует лемма, которая
гласит: Если случайная величина
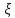 имеет плотность распределения
имеет плотность распределения
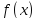 ,
то случайная величина
,
то случайная величина
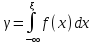 имеет равномерный закон распределения
на интервале
имеет равномерный закон распределения
на интервале
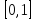 , т.е.
, т.е.
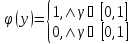
Также существует теорема.
Пусть
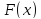 - функция распределения некоторой
случайной величины
- функция распределения некоторой
случайной величины
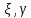 – случайная величина с равномерным
законом распределения на интервале
– случайная величина с равномерным
законом распределения на интервале
 .
Тогда случайная величина
.
Тогда случайная величина
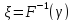 ,
где
,
где
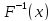 - обратная функция
- обратная функция
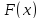 ,
подчиняется закону распределения
,
подчиняется закону распределения
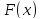 .
.
Исходя из этого, случайное
число
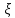 ,
подчиняющееся закону
,
подчиняющееся закону
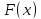 ,
определяют по формуле:
,
определяют по формуле:
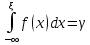 .
.
Решение с помощью обратных функций
Если учесть, что на практике
функция
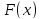 – монотонно возрастающая, то можно для
заданного времени безотказной работы
– монотонно возрастающая, то можно для
заданного времени безотказной работы
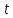 найти значения
найти значения
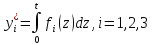 .
.
Тогда проверка работоспособности
элементов сведется к проверке условия
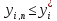 ,
где
,
где
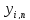 - равномерно распределенное на промежутке
- равномерно распределенное на промежутке
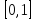 случайное число,
случайное число,
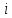 - номер элемента,
- номер элемента,
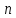 - номер очередной реализации случайного
процесса.
- номер очередной реализации случайного
процесса.
Это равносильно условию
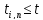 ,
причем процедура вычисления обратной
функции здесь не требуется.
,
причем процедура вычисления обратной
функции здесь не требуется.
Можно также существенно
упростить логическое выражение, если
перейти от события «безотказная работа
системы» к событию «отказ системы».
Отказ системы означает истинность
выражения
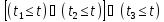
С учетом данных упрощений, алгоритм принимает следующий вид:
-
По заданному времени безотказной работы
 вычислить
вычислить
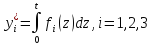
-
Положить
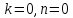 .
. -
Получить три равномерно распределенных на
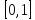 случайных числа
случайных числа
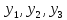
-
Проверить истинность логического выражения
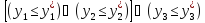
Если оно истинно, то положить
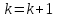 и перейти к шагу 5, иначе просто перейти
к шагу 5.
и перейти к шагу 5, иначе просто перейти
к шагу 5.
-
Положить
 .
. -
Если
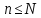 ,
то перейти к шагу 3, иначе вычислить и
вывести
,
то перейти к шагу 3, иначе вычислить и
вывести
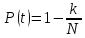 .
.
-
Стоп.
При построении закона
распределения эти действия необходимо
повторять последовательно для всех
значений t от 0, пока
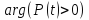 ,
т. е до момента, когда вероятность
безотказной работы опустится до значения
0.
,
т. е до момента, когда вероятность
безотказной работы опустится до значения
0.
Сглаживание функции
Метод наименьших квадратов
Пусть имеется
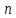 значений некоторой переменной
значений некоторой переменной
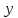 и соответствующих переменных
и соответствующих переменных
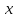 .
Задача заключается в том, чтобы взаимосвязь
между
.
Задача заключается в том, чтобы взаимосвязь
между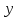 и
и
 аппроксимировать некоторой функцией
аппроксимировать некоторой функцией
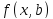 ,
известной с точностью до некоторых
неизвестных параметров
,
известной с точностью до некоторых
неизвестных параметров
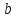 ,
то есть фактически найти наилучшие
значения параметров
,
то есть фактически найти наилучшие
значения параметров
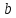 ,
максимально приближающие значения
,
максимально приближающие значения
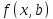 к фактическим значениям
к фактическим значениям
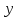 .
.
Фактически, это сводится к
случаю «решения» переопределенной
системы уравнений относительно
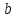 :
:
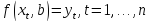
В регрессионном анализе
используются вероятностные модели
зависимости между переменными
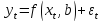 ,
где
,
где
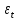 – случайные ошибки модели.
– случайные ошибки модели.
Соответственно, отклонения
наблюдаемых значений
 от модельных
от модельных
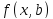 предполагаются уже в самой модели.
Сущность метода наименьших квадратов
заключается в том, чтобы найти такие
параметры
предполагаются уже в самой модели.
Сущность метода наименьших квадратов
заключается в том, чтобы найти такие
параметры
 ,
при которых сумма квадратов отклонений
,
при которых сумма квадратов отклонений
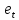 будет минимальной:
будет минимальной:
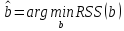 , где
, где
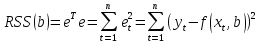 .
.
В общем случае решение этой
задачи может осуществляться численными
методами оптимизации (минимизации). В
этом случае говорят о нелинейном
методе наименьших квадратов.
Во многих случаях можно получить
аналитическое решение. Для решения
задачи минимизации необходимо найти
стационарные точки функции
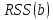 R
S
S
( b
) {\displaystyle
RSS(b)},
продифференцировав её по неизвестным
параметрам
R
S
S
( b
) {\displaystyle
RSS(b)},
продифференцировав её по неизвестным
параметрам
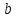 b
{\displaystyle
b},
приравняв производные к нулю и решив
полученную систему уравнений:
b
{\displaystyle
b},
приравняв производные к нулю и решив
полученную систему уравнений:

Преобразовав данное уравнение,
получим:
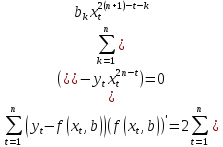
Перепишем систему в виде:
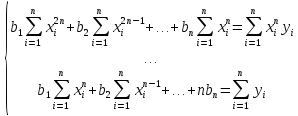
В итоге получилась система
 уравнений, которую можно решить, например,
методом Крамера.
уравнений, которую можно решить, например,
методом Крамера.
Метод Крамера
Мы можем использовать данный
метод, поскольку, в данном случае, имеется
система
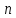 уравнений с
уравнений с
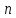 неизвестными, и каждый элемент отличается
от нуля.
неизвестными, и каждый элемент отличается
от нуля.
Cистему уравнений нужно
записать в виде произведения матриц:
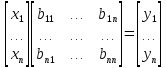
Найдем определитель данной
матрицы ( ).
Для этого нужно привести матрицу к
треугольному виду, затем перемножить
элементы главной диагонали.
).
Для этого нужно привести матрицу к
треугольному виду, затем перемножить
элементы главной диагонали.
Элементы
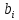 можно найти следующим образом:
можно найти следующим образом:
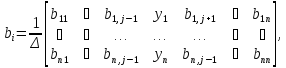
где j-ый столбец матрицы системы заменяется столбцом свободных членов.
Получение полинома
После решения системы методом
Крамера, необходимо подставить найденные
значения
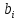 в полином вида:
в полином вида:
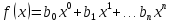
Среднее время работы системы
В теории надежности под этим
термином понимается математическое
ожидание времени исправной работы
системы:
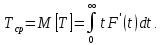
Практически, среднее время
исправной работы системы равно:
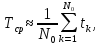
где
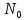 - количество испытаний над системой.
- количество испытаний над системой.
Вероятность работы системы на промежутке времени
На промежутке времени
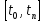 ,
вероятность работы системы определяется
как отношение вероятности работы за
позднее время к вероятности работы за
раннее время:
,
вероятность работы системы определяется
как отношение вероятности работы за
позднее время к вероятности работы за
раннее время:
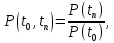
где
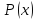 – вероятность работы системы за время
– вероятность работы системы за время
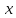 .
.
