
- •Московский авиационный институт (национально исследовательский университет)
- •Курсовой проект
- •Содержание
- •Техническое задание
- •Технические требования
- •Условия эксплуатации
- •Объем работы
- •Назначение и описание механизма
- •Литература
- •Проектирование зубчатой передачи
- •Проектный расчет зубчатой передачи
- •Выбор материал зубчатой передачи
- •Выбор относительной ширины зубчатого венца
- •Выбор степени точности зацепления
- •Выбор формы выполнения зуба
- •Определение чисел зубьев шестерни,колесаи передаточного числа
- •Определение предельных контактных напряжений на поверхностях зубьев в редукторе
- •Определение допускаемого контактного напряжения
- •Определение значение коэффициентов,,и функции, входящих в формулу межосевого расстояния цилиндрической передачи
- •Определение в первом приближении межосевого расстоянияцилиндрической зубчатой пары
- •Определение допускаемых напряжений изгиба в расчетных точках зубьев шестерни и колеса
- •Проверка изгибной прочности зубьев
- •Проектирование вала механизма
- •Проектировочный расчет валов механизма
- •Проверочный расчет вала на прочность
- •Расчет подшипников на долговечность
- •Расчет эвольвентных шлицевых соединений
Определение в первом приближении межосевого расстоянияцилиндрической зубчатой пары

 – расчетный вращательный момент на
ведущем звене передачи:
– расчетный вращательный момент на
ведущем звене передачи:

Где:
 - номинальный вращательный момент на
ведущем звене передачи:
- номинальный вращательный момент на
ведущем звене передачи:
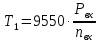



 – предельный модуль упругости материала
шестерни и колеса, для стали.
– предельный модуль упругости материала
шестерни и колеса, для стали.

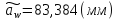
Определение модуля зубчатой передачи
В первом приближении для цилиндрической передачи находится как:

Округляем до ближайшего значения по таблице получаем:
m=1,75
Определение основных геометрических размеров зубчатой передачи
 – делительный диаметр шестерни
– делительный диаметр шестерни
 – диаметр окружности шестерни вершин
зубьев
– диаметр окружности шестерни вершин
зубьев
 – диаметр окружности шестерни впадин
зубьев
– диаметр окружности шестерни впадин
зубьев
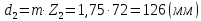 – делительный диаметр колеса
– делительный диаметр колеса
 – диаметр окружности колеса вершин
зубьев
– диаметр окружности колеса вершин
зубьев
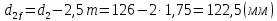 – диаметр окружности колеса впадин
зубьев
– диаметр окружности колеса впадин
зубьев

Уточненное
межосевое расстояние с учетом поправок

 – рабочая ширина венца в первом
приближении
– рабочая ширина венца в первом
приближении
По таблице определяем стандартизированные значение ширины, один венец шире другого для учитывания возможного осевого смещения:


Проверочный расчет зубьев передачи на контактную прочность.
Проверочный расчет проводится после выполнения эскиза механизма с конструкторской проработкой.
Условие контактной прочности рабочих поверхностей зубьев.
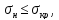
Где:
 – расчетное контактное напряжения
– расчетное контактное напряжения
 – допускаемое контактное напряжение
– допускаемое контактное напряжение

Определение коэффициентов

Коэффициент
 ,
учитывающий форму сопряженных
поверхностей зуба:
,
учитывающий форму сопряженных
поверхностей зуба:

Для цилиндрических передач:
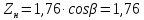
Коэффициент
 ,
учитывающий упругие свойства материалов
зубьев:
,
учитывающий упругие свойства материалов
зубьев:

Коэффициент
 ,
учитывающий суммарную длину контактных
линий и зацеплении:
,
учитывающий суммарную длину контактных
линий и зацеплении:

Удельная окружная сила при определении контактных напряжений


Где:
 – окружная сила в зацеплении (Н). Для
цилиндрической передачи:
– окружная сила в зацеплении (Н). Для
цилиндрической передачи:

Коэффициенты
 и
и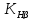 определены вП. 1.8.
определены вП. 1.8.Коэффициент
 :
:

Где:
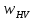 – удельная окружная динамическая
нагрузка:
– удельная окружная динамическая
нагрузка:

Где:
 – коэффициент, учитывающий модификацию
головки зуба и твердость рабочих
поверхностей, выбирается по таблице.
– коэффициент, учитывающий модификацию
головки зуба и твердость рабочих
поверхностей, выбирается по таблице.
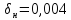
 – коэффициент, учитывающий погрешность
зацепления по шагу, выбирается по
таблице.
– коэффициент, учитывающий погрешность
зацепления по шагу, выбирается по
таблице.

 – окружная скорость в зацеплении, для
цилиндрической передачи:
– окружная скорость в зацеплении, для
цилиндрической передачи:




Определение расчетного контактного напряжения
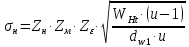

Проверка контактной прочности зубьев


⇒условие прочности выполнено
Переопределение расчетную ширину колес:

Значение
 и
и практически совпадают (20,985 (мм) и 21 (мм)),
что говорит о практически оптимальном
изделии, которое мы разрабатываем.
практически совпадают (20,985 (мм) и 21 (мм)),
что говорит о практически оптимальном
изделии, которое мы разрабатываем.
Проверочный расчет зубьев передачи на прочность зубьев по изгибу
Условие изгибной прочности

Где:
 – расчетное контактное напряжение на
переходной поверхности у основания
зуба со стороны растяжения.
– расчетное контактное напряжение на
переходной поверхности у основания
зуба со стороны растяжения.
 – допускаемое контактное напряжение.
– допускаемое контактное напряжение.
Определение расчетного изгибного напряжения


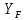 – коэффициент формы зуба:
– коэффициент формы зуба:
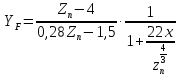
Где:

Для шестерни:


Для колеса:


 – коэффициент, учитывающий наклон
линии зуба:
– коэффициент, учитывающий наклон
линии зуба:

Где
в прямозубых β=0 -

 – удельная расчетная окружная нагрузка:
– удельная расчетная окружная нагрузка:

Где:
 – коэффициент, учитывающий распределение
нагрузки между зубьями при расчете на
изгиб. Для прямых зубьев:
– коэффициент, учитывающий распределение
нагрузки между зубьями при расчете на
изгиб. Для прямых зубьев:
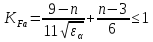
Где:
 – степень точности передачи
– степень точности передачи

 – коэффициент торцевого перекрытия
– коэффициент торцевого перекрытия

Где:
 – частые коэффициенты, выбираемые из
графика, в зависимости от
– частые коэффициенты, выбираемые из
графика, в зависимости от и
и :
:


 – коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба,
принимают
– коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба,
принимают

 – коэффициент, учитывающий дополнительную
динамическую нагрузку на зуб:
– коэффициент, учитывающий дополнительную
динамическую нагрузку на зуб:

Где:
 – удельная окружная динамическая
нагрузка. Для цилиндрических передач:
– удельная окружная динамическая
нагрузка. Для цилиндрических передач:

Где:
 – для прямых зубьев с модификацией
– для прямых зубьев с модификацией

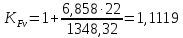


Расчетные местные напряжения изгиба у основания у зуба шестерни и колеса
 и
и


