3 Формирование математической модели

Поскольку исследование двухкаскадного усилителя предполагает построение и анализ частотных характеристик основных схемных функций, целесообразно формировать математическая модель усилителя для полного диапазона частот. Так как работа усилителя происходит в режиме малого переменного сигнала, то рабочая точка биполярного транзистора не выходит за пределы линейных участков вольт-амперных характеристик. В таком режиме усилитель относится к квазилинейным электронным схемам и его анализ можно выполнить с достаточной точностью на основе линейной математической модели операторными методами. Принимая во внимание численный характер требуемых результатов и доступность средств вычислительной техники, будем использовать матричные методы формирования и реализации математической модели.

Схема замещения усилителя по переменному току для анализа в узловом базисе представлена на рис. 3.1

Рис.3.1. Схема замещения двухкаскадного усилителя.

В схеме замещения все двухполюсные компоненты представлены как у-компоненты: источник входного сигнала – ветвью, содержащей параллельно включенные идеальный источник переменного тока j_c и внутреннюю проводимость g_c пассивные двухполюсники - соответствующими проводимостями g2=1/R2, g3=1/R3 и т.д., Yн.

Эквивалентные значения в схеме замещения представлены в виде:

Определение выражений схемных функций обобщенным матричным метод в узловом базисе.

Поскольку сформированная схема замещения по переменному току содержит 7 узлов, система координат содержит 6 независимых сечений. Выберем каноническую систему сечений, для чего пронумеруем узлы схемы и один из них (узел 0) выберем в качестве базисного.

Укороченная матрица проводимостей для пассивной части схемы:

pC1	-pC1	0	0	0	0
-pC1	pC1+	0		0	0
0	0	g3	0	0	0
0		0		0	-pC2
0	0	0	0		0
0	0	0	-pC2	0	pC2

Неопределённая матрица проводимостей биполярного транзистора VT1:

Неопределённая матрица проводимостей биполярного транзистора VT2:

Получаем укороченную матрицу проводимостей:

pC1	-pC1	0	0	0	0
-pC1	pC1++ y11	-(y11+y12)		0	0
0	-(y11+y21)	g3+y11+y12+ y21+y22+y11’	y12’	-(y11’+y12’)	0
0		y21’		-(y21’+y22’)	-pC2
0	0	-(y11’+y21’)	-(y12’+y22’)	+y11’+y12’+ y21’+y22’	0
0	0	0	-pC2	0	pC2

4 Определение схемных функций

Рассматриваемый избирательный усилитель по назначению относится к усилителям напряжения, поэтому основными схемными функциями, характеризующими его качественные технические показатели, являются коэффициент передачи напряжения, входной импеданси выходной импеданс.

Указанные схемные функции вычисляются на основе определителя и алгебраических дополнений укороченной матрицы эквивалентных сопротивлений. Поскольку ветви источника сигнала и нагрузки являются внешними ветвями схемы замещения, для схемных функций справедливы соотношения:

,

,

,

где 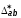– простое несимметричное,,– простые симметричные,– двухкратное простое симметричное алгебраические дополнения укороченной матрицы эквивалентных сопротивлений схемы;– определитель укороченной матрицы эквивалентных сопротивлений схемы;– номер входного цикла;– номер выходного цикла.

Для выбранной на схеме замещения (рис. 3.3) системы независимых циклов ,,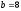 поэтому выражения для схемных функций принимают вид:

,

,

.