Математика, мат.анализ / Математика
.doc1 вариант
1. Если
,
,
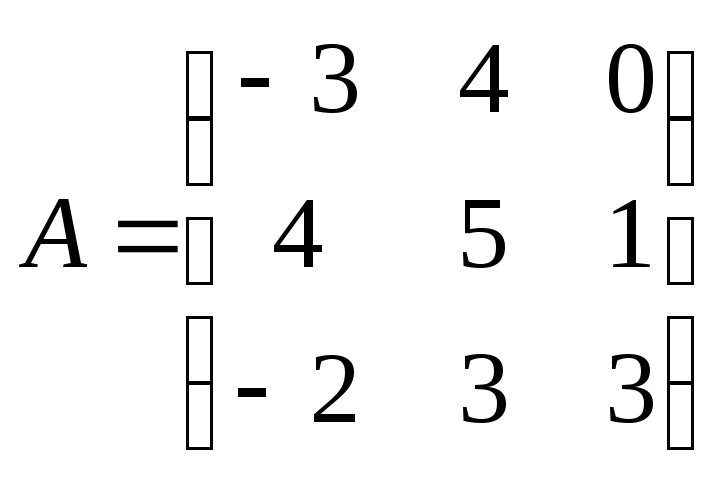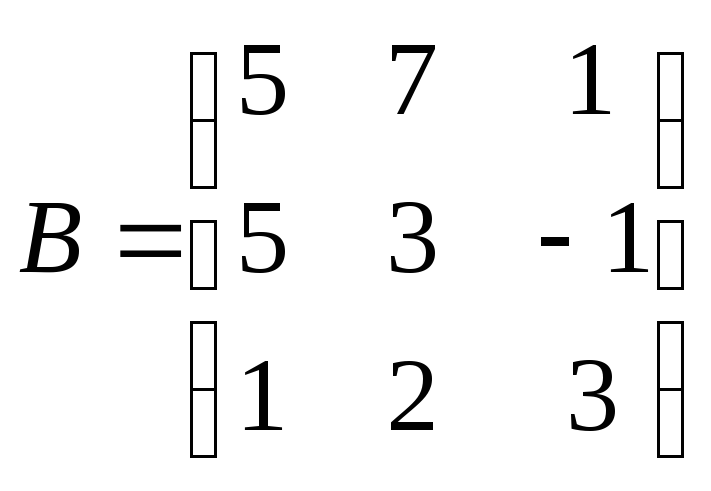то сумма
равна:
A)
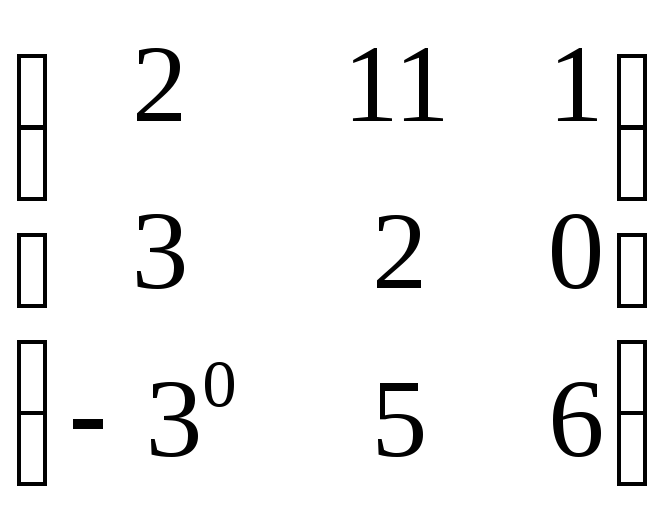
B)*
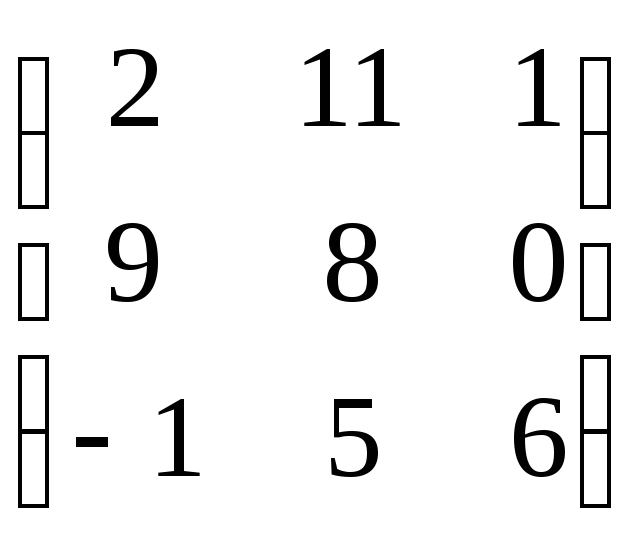
C)*
D)
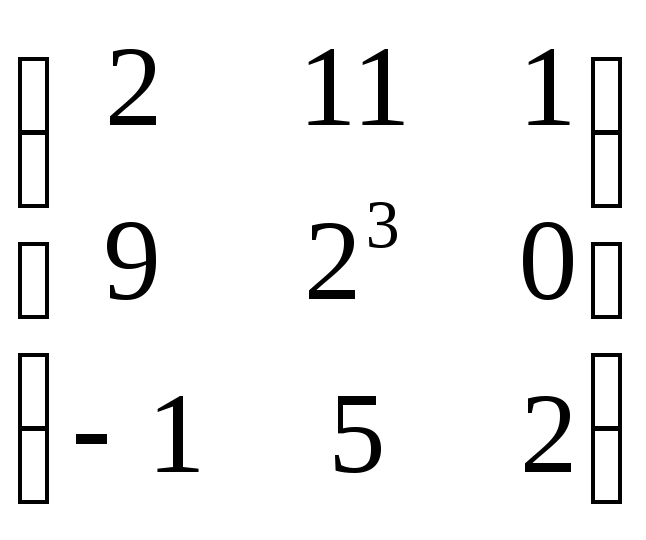
E)*
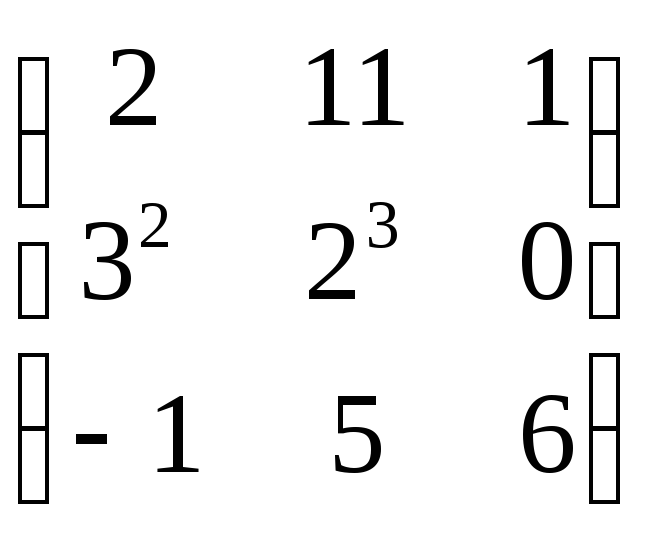
2. Значение определителя
равно:
A)*
B)*
C)
D)
E)
F)
G)
3. Если
,
,
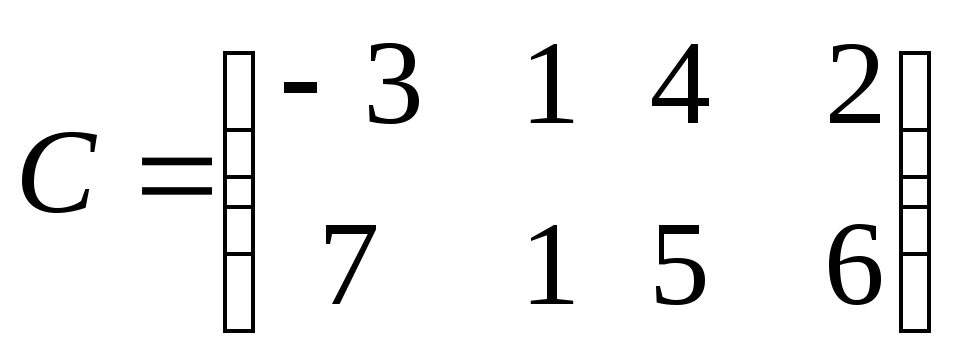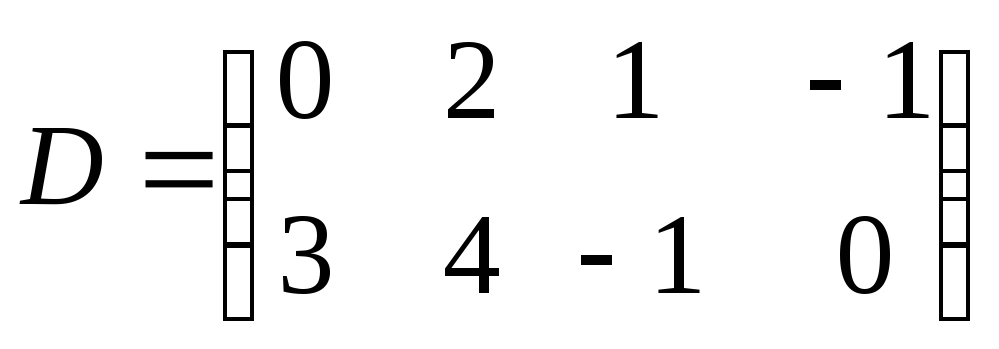то разность
равна:
A)
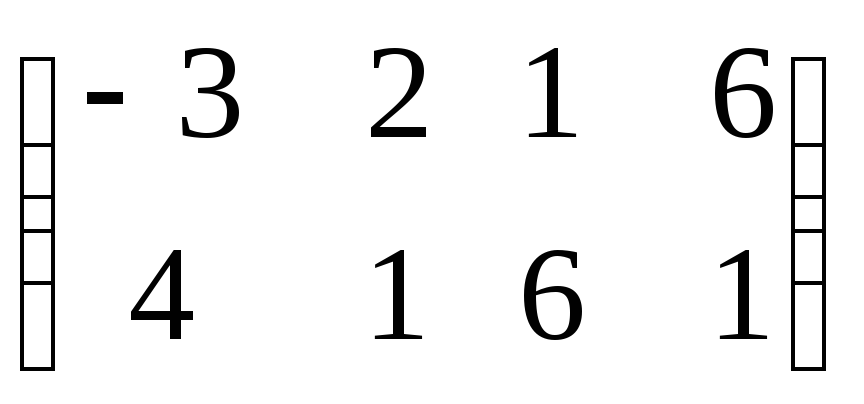
B)*
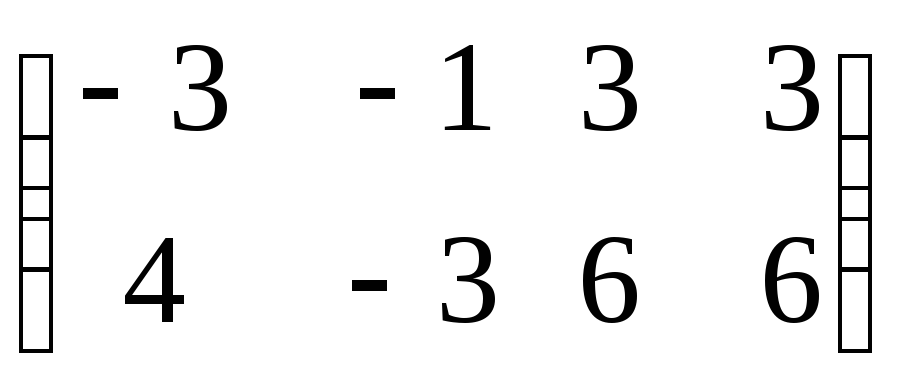
C)
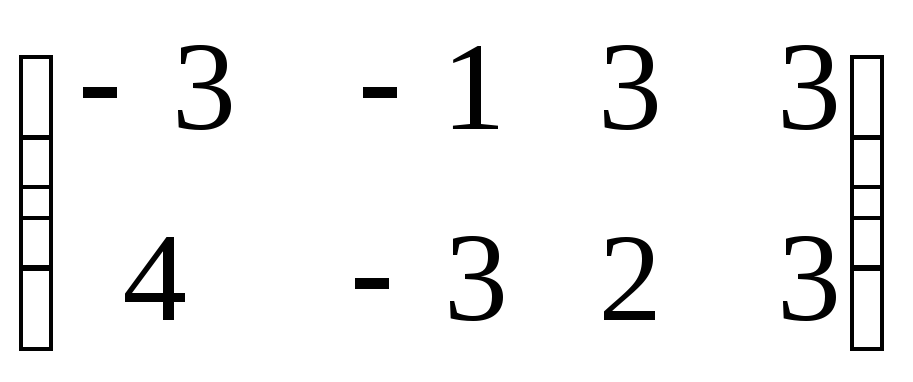
D)
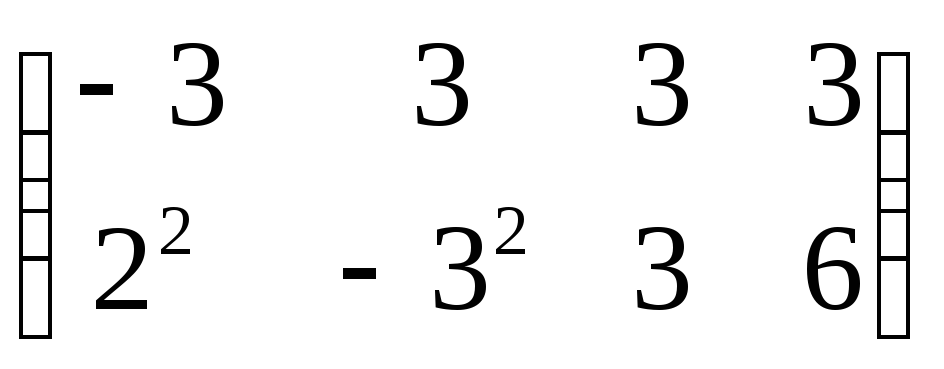
E)*
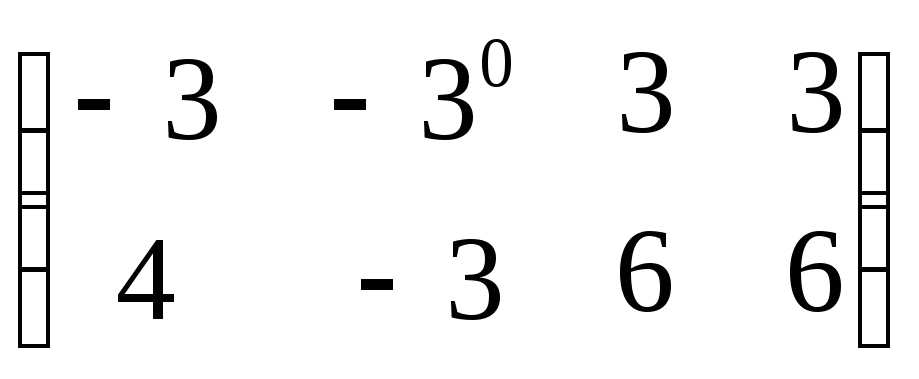
F)*
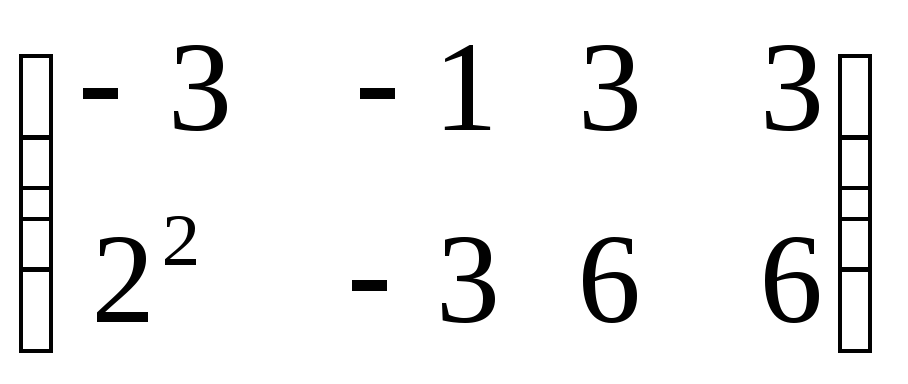
4. Определитель 3-го порядка
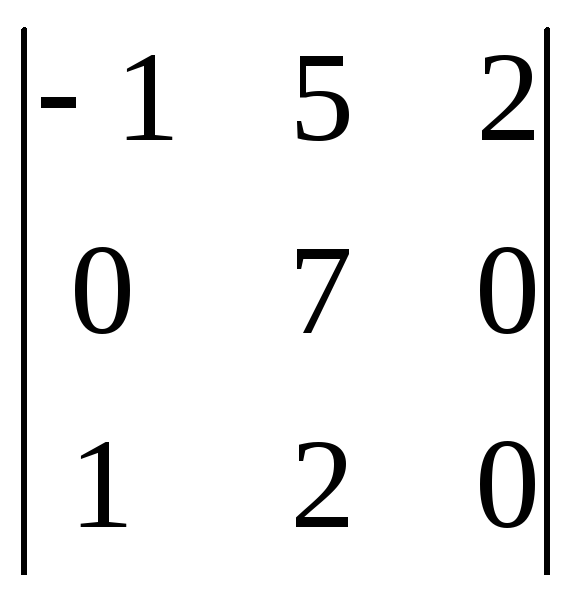равен:
A)*
B)*
C)
D)
E)*
5.
является:
A) уравнением Бернулли
B)* дифференциальным уравнением с разделяющимися переменными
C) дифференциальным уравнением второго порядка
D) неоднородным дифференциальным уравнением
E) дифференциальным уравнением в частных производных
6. Однородной функцией нулевого измерения является:
A)
B)
C)*
D)*
E)*
7. Один из корней характеристического уравнения равен нулю для дифференциального уравненипя(-ий):
A)
B)*
C)
D)
E)*
F)*
8. Решением дифференциального
уравнения
является функция:
A)
B)*
C)*
D)
E)
F)
G)
9. Матрица
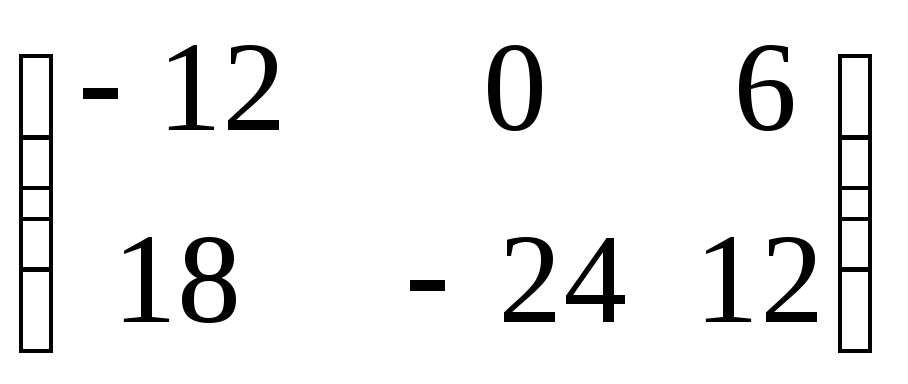равна
произведению:
A)*
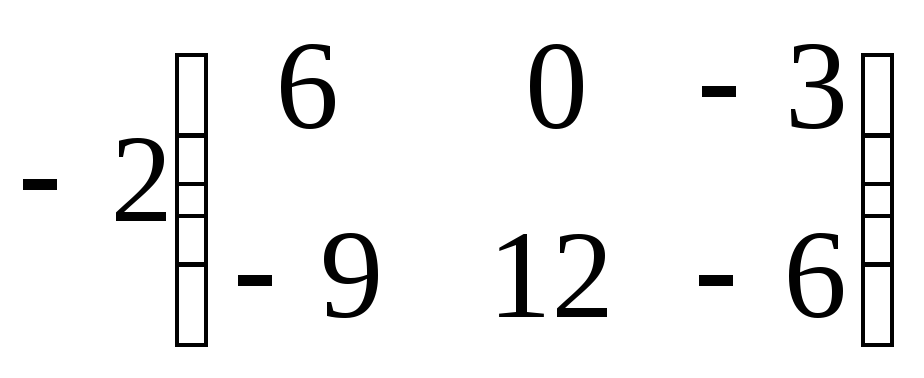
B)
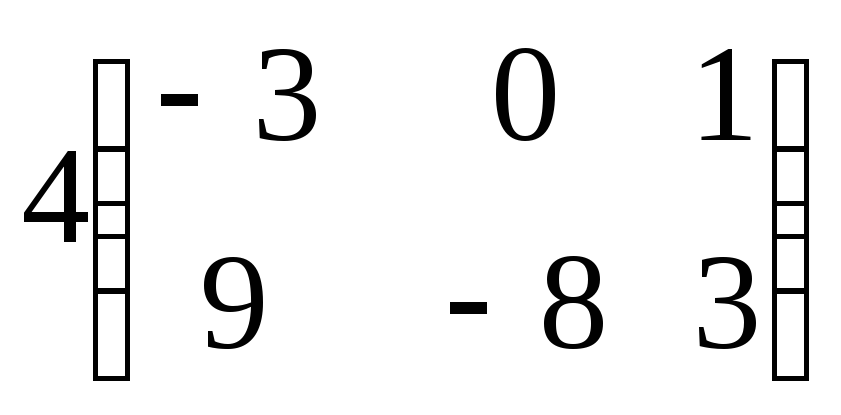
C)
D)*
E)
F)*
G)
10. Длина вектора
A)*
B)
C)*
D)*
E)
F)
G)
11. Даны векторы
и
.
Значение скалярного произведения
векторов
и
принадлежат интервалу
для векторов:
A)
и
B)
и
C)*
и
D)
и
E)*
и
F)
и
G)
и
12. Прямая
:
A) перпендикулярна
прямой
B)* отсекает на
оси
отрезок
C)* отсекает на
оси
отрезок
D) параллельна
прямой
E) отсекает на
оси
отрезок
F) отсекает на
оси
отрезок
13. Точка
является серединой отрезка, заданного
точками:
A)
и
B)
и
C)*
и
D)*
и
E)
и
F)*
и
14. Точка
является центром окружности:
A)*
B)
C)*
D)
E)
F)
15. Значение предела:
A)*
B)*
C)
D)
E)
F)
G)*
16. Интервал убывания функции
A)
B)*
C)
D)
E)
17. Один из эктремумов функции
находится в точке:
A)
B)
C)
D)*
E)*
18. Дано
.
Тогда
:
A)
B)*
C)
D)*
E)
F)
19. Значение предела:
A)*
B)
C)
D)*
E)
F)*
G)
20. Значение объема тела,
полученного при вращении вокруг оси
фигуры, ограниченной линиями
принадлежат промежутку:
A)* (73;76)
B) (77;80)
C) (70;73)
D) (72;75)
E) (76;79)
F) (71;74)
21. Тело движется прямолинейно
со скоростью
м/с. Тогда путь S,
пройденный телом за промежуток времени
,
равен:
A)
,
B)*
,
C)
,
D)
,
E)
,
F)*
,
G)
,
22. Значение длины дуги кривой
,
отсеченной прямой
принадлежит
промежутку:
A) (5;8)
B) (7;10)
C)* (1;3)
D) (6;9)
E)* (2;5)
23. Значение площади фигуры,
ограниченной линиями
,
принадлежит промежутку:
A) (16;19)
B) (17;20)
C) (21;24)
D)* (19;22)
E)* (18;21)
24. Одна из стационарных точек
функции
имеет координаты:
A)* (0;0)
B) (2;-1)
C) (2;-1)
D) (-1;-1)
E) (2;2)
F) (1;1)
25. Для функции
верны утверждения(-ие):
A)* (-1;2)-экстремума нет
B) (-1;-1)-точка максимума
C) (-2;-2)-точка максимума
D) (2;2)-точка минимума
E) (2;-1)-экстремума нет
F) (1;1)-точка минимума
26. Если
,
,
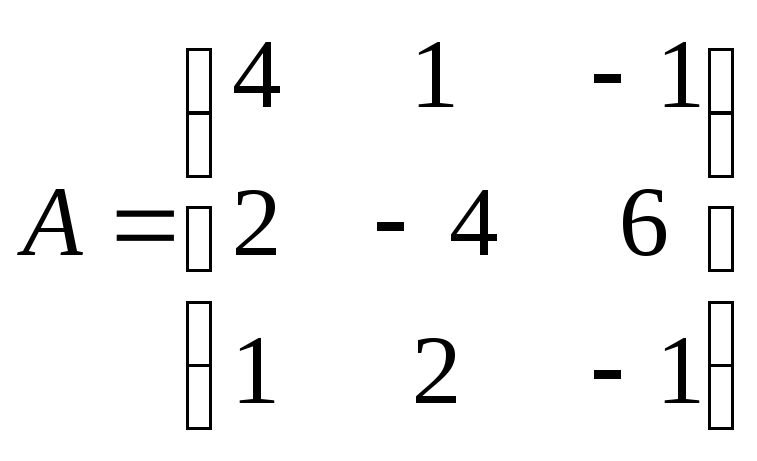то сумма
равна:
A)*
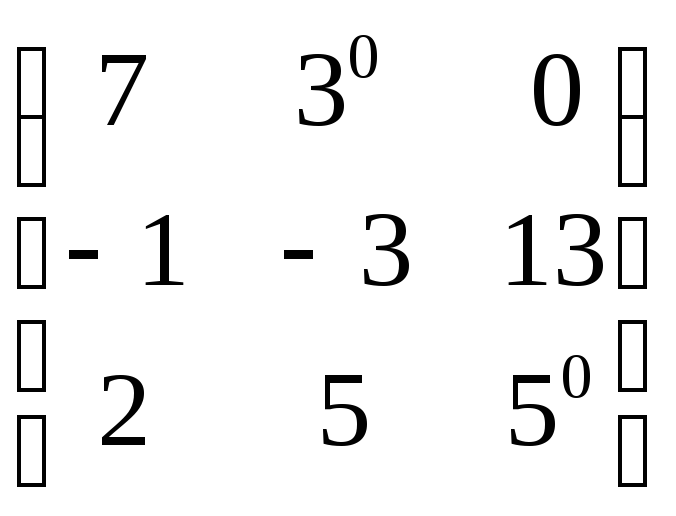
B)*
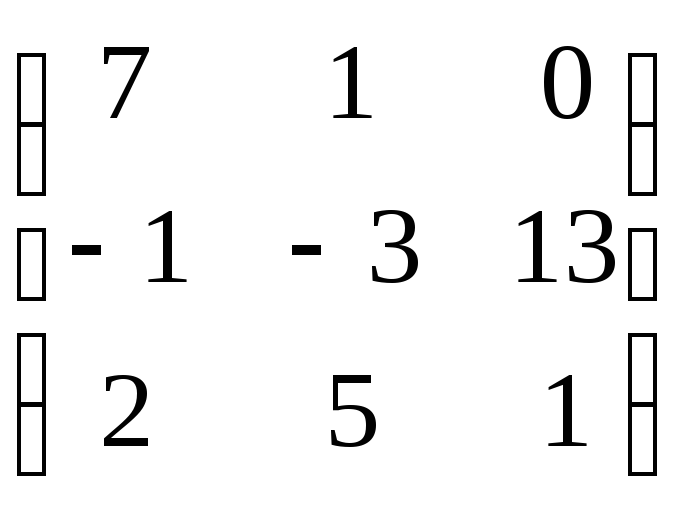
C)
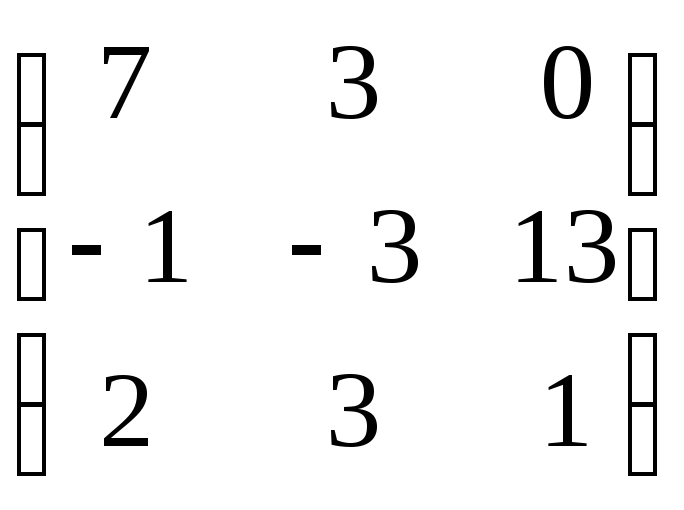
D)
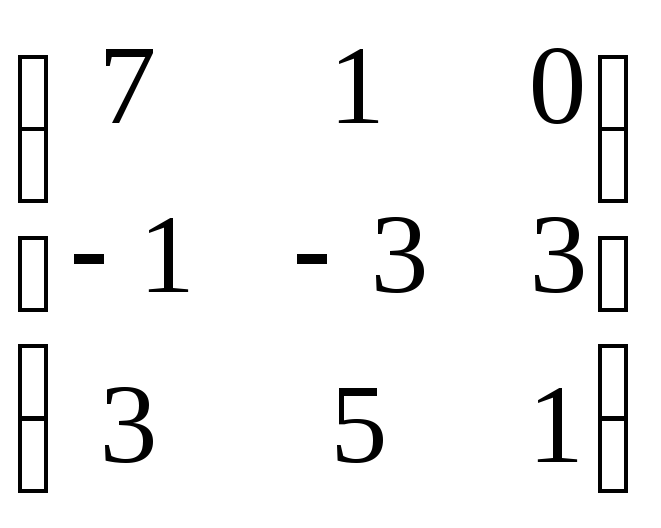
E)
F)
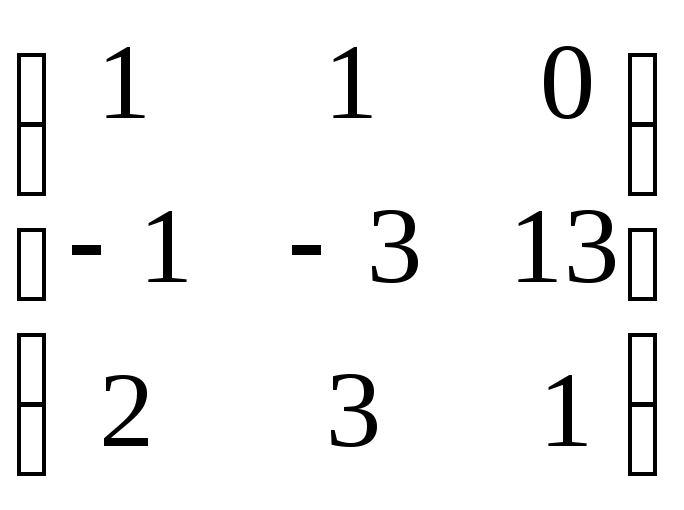
27. Система
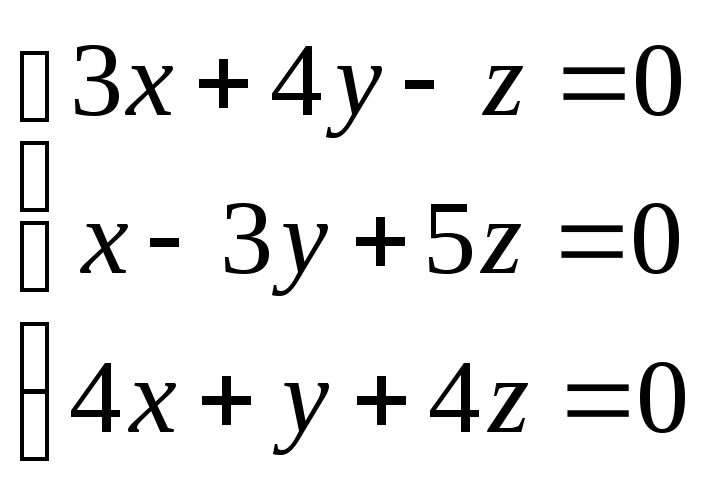
A) вырожденная
B)* имеет единственное нулевое решение
C) несовместна
D) невырожденная
E)* однородная
28. Матричный метод для решения систем линейных алгебраических уравнении можно применить, если:
A)* система однородная и основная матрица системы невырожденная
B) система неоднородная и основная матрица системы вырожденная
C) основная матрица системы вырожденная и ранг основной матрицы не равен рангу расширенной матрицы
D) количество неизвестных меньше количества уравнений в системе
E) количество неизвестных больше количества уравнений в системе
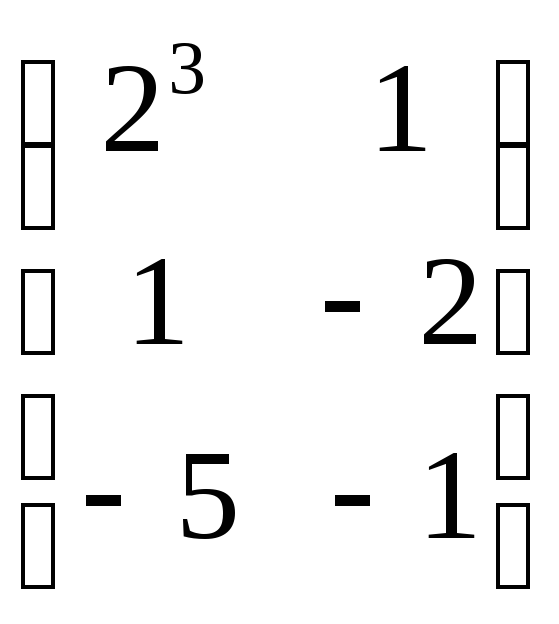
29. Если
,
,
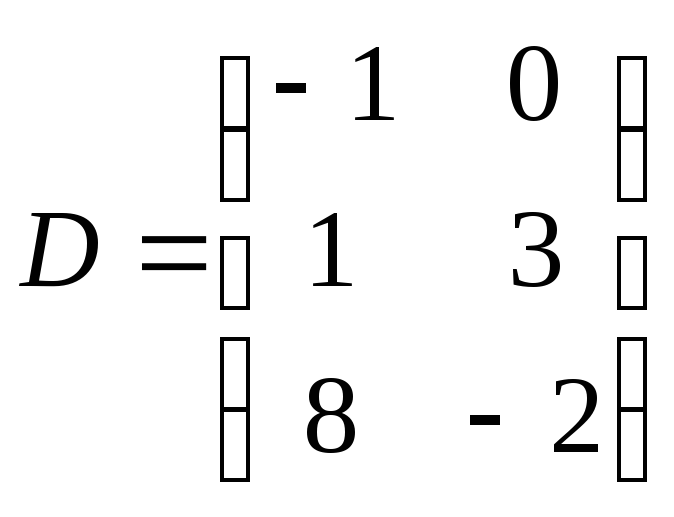то разность
A)
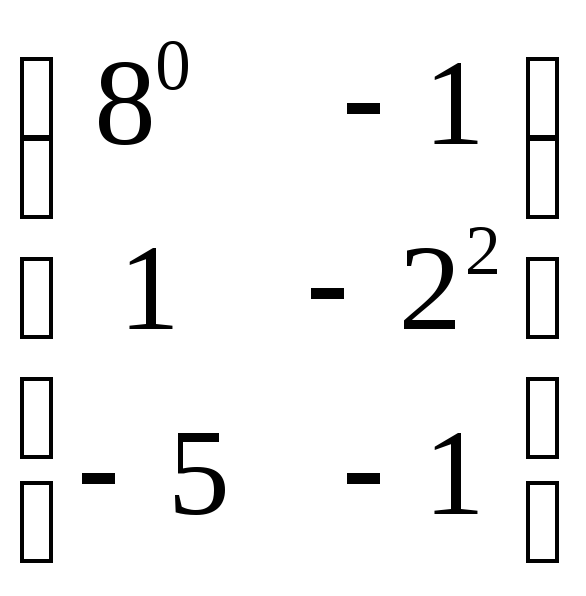
B)*
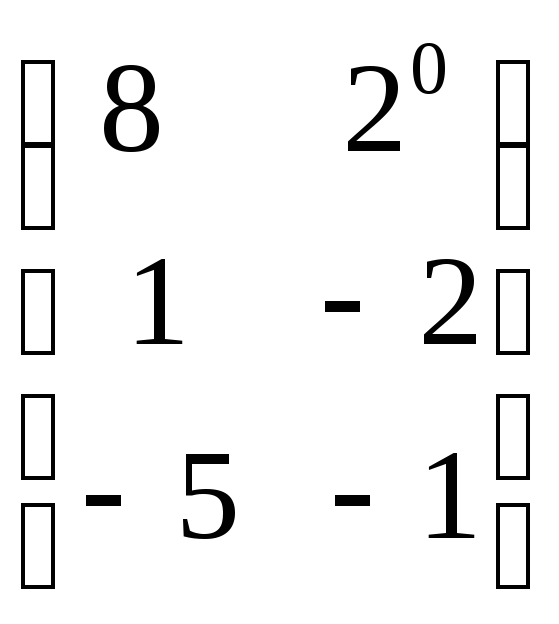
C)
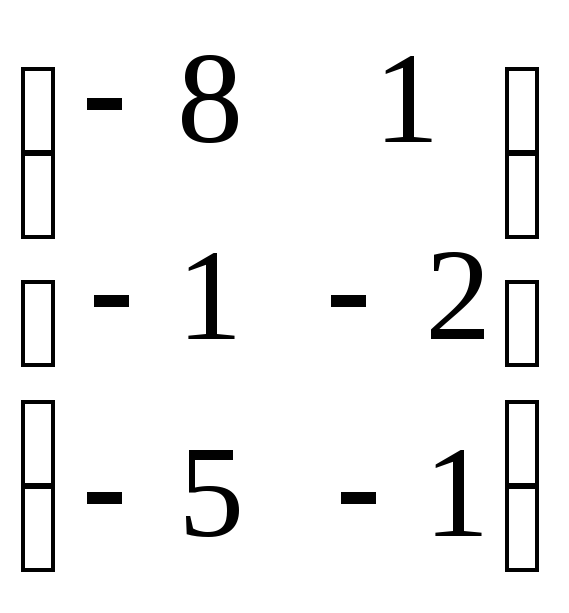
D)*
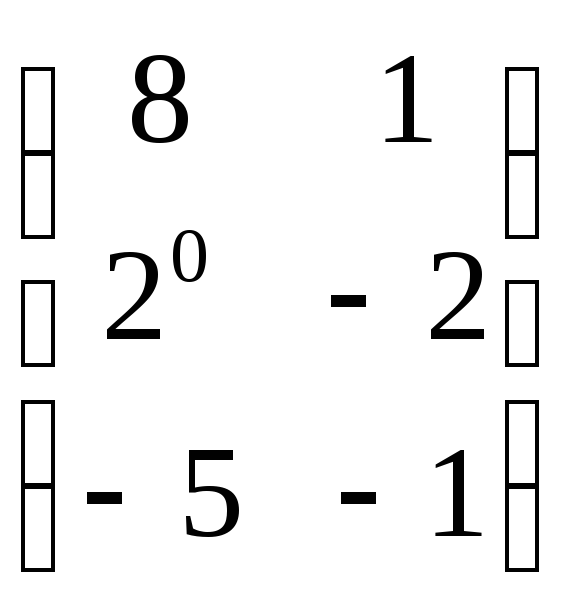
E)*
30. Дифференциальным уравнением второго порядка является:
A)
B)
C)*
D)*
E)
F)
31. Дифференциальным уравнением третьего порядка является:
A)
B)
C)
D)*
E)
32. Порядок дифференциального
уравнения
равен числу из промежутка:
A)*
B)
C)*
D)
E)*
33. Дифференциальным уравнением первого порядка является:
A)
B)*
C)
D)*
E)
F)*
34. Значение определителя
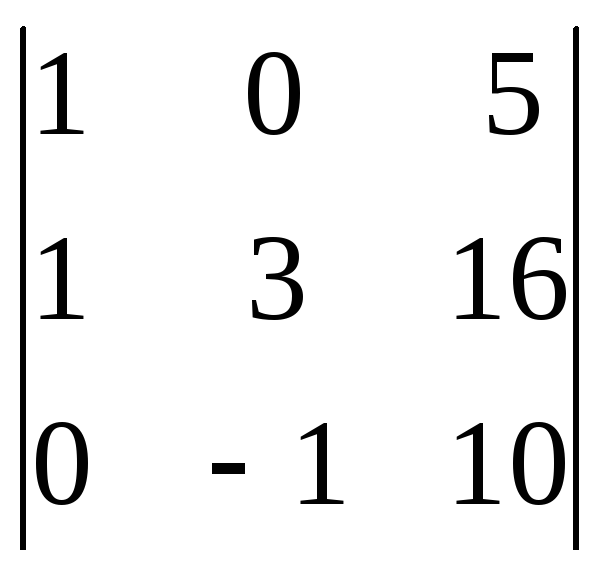равно:
A)
B)
C)
D)*
E)
F)
G)*
35. Даны векторы
,
.
Тогда для скалярного произведения
справедливо:
A)
B)
C)*
D)
E)
F)
36. Скалярное произведение
векторов:
,
A)
B)
C)*
D)
E)
F)
37. Точки
и
лежат на прямой:
A)*
B)
C)*
D)
E)
F)*
G)
38. Плоскость
:
A) параллельна
вектору
B)* параллельна
вектору
C) отсекает на
оси
отрезок
D) отсекает на
оси
отрезок
E)* отсекает на
оси
отрезок
F) отсекает на
оси
отрезок
G) отсекает на
оси
отрезок
39. Число
является радиусом окружности:
A)
B)*
C)
D)
E)
F)*
G)
40. Значение предела
принадлежит интервалу:
A)* (1;4)
B)* (0;3)
C) (-2;1)
D) (-3;0)
E) (-1;2)
F) (4;7)
G)* (2;5)
41. Угловой коэффициент
касательной к кривой
в точке
равен:
A)*
B)*
C)*
D)
E)
F)
G)
42. Вторая производная функции
в точке
равна:
A)
B)
C)
D)*
E)*
F)*
43. Значение предела:
A)
B)
C)*
D)
E)
F)
44. Предел
равен:
A)
B)*
C)
D)
E)*
45. Значение объема тела,
полученного при вращении вокруг оси OX
фигуры, ограниченной линиями
,
принадлежит промежутку:
A)* (3;6)
B) (5;8)
C) (0;3)
D)* (1;4)
E) (4;7)
F) (6;9)
46. Интеграл
равен:
A)
B)
C)
D)*
E)*
47. Площадь фигуры, ограниченной
линиями
,
,
равна:
A) 2,6
B) 2,(7)
C) 2,7
D)* 2,(6)
E)*
F)*
48. Площадь фигуры, ограниченной
линиями
,
равна: