
Лаба№3 ЛЛт разложение
.docxФГБОУ ВПО Национальный исследовательский университет
«Московский Энергетический институт»
Институт автоматики и вычислительной техники
Кафедра математического моделирования
Лабораторная работа №3
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПРЯМЫМИ МЕТОДАМИ. ТЕОРИЯ ВОЗМУЩЕНИЙ
Вариант 22
Задача 3.2
Выполнил: студент группы ТФ-12-16
Лукоянов Е.Э.
Проверил: Амосова О.А.
Москва 2017
Постановка задачи
Решить
систему
Ax=b
с матрицей A
и вектором b
методом
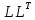 -разложения.
-разложения.
Элементы
матрицы вычисляются
по
формулам:
вычисляются
по
формулам:
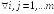 ,
где
,
где
 -
порядок матрицы,
-
порядок матрицы,
 —
параметр, указанный в индивидуальном
варианте.
—
параметр, указанный в индивидуальном
варианте.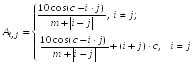
Вектор
правой части взять с компонентами
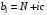 ,
,
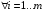 ,
где N
– номер варианта, c-параметр.
N=22,
m=24,
c=6.1
,
где N
– номер варианта, c-параметр.
N=22,
m=24,
c=6.1
Необходимый теоретический материал
Если
матрица системы является симметричной
и положительно определенной, то для
решения системы применяют метод
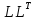 -разложения
. В основе метода лежит алгоритм
специального LU-разложения
матрицы A,
в результате чего она приводится к виду
A=
-разложения
. В основе метода лежит алгоритм
специального LU-разложения
матрицы A,
в результате чего она приводится к виду
A=![]() .
Если разложение получено, то как и в
методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными
матрицами:
.
Если разложение получено, то как и в
методе LU-разложения,
решение системы сводится к последовательному
решению двух систем с треугольными
матрицами:
![]() и
и
![]() Для нахождения коэффициентов матрицы
L неизвестные
коэффициенты матрицы
Для нахождения коэффициентов матрицы
L неизвестные
коэффициенты матрицы
![]() приравнивают
соответствующим элементам матрицы A.
Затем последовательно находят требуемые
коэффициенты по формулам:
приравнивают
соответствующим элементам матрицы A.
Затем последовательно находят требуемые
коэффициенты по формулам:
![]() ,
,
![]() i = 2, 3, ..., m,
i = 2, 3, ..., m,
![]() ,
,
![]() i = 3, 4, ..., m,
i = 3, 4, ..., m,
![]()
![]() i = k+1, .., m.
i = k+1, .., m.
![]()
Результаты вычислительного процесса
Полученная матрица А и вектор b имеют вид:
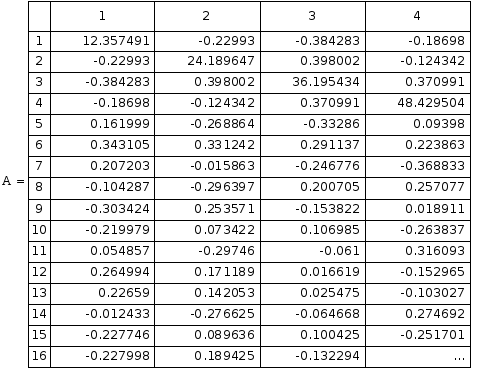
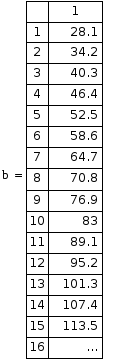
Результаты вычислительного процесса
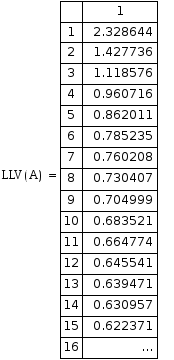
Анализ полученных результатов
С помощью встроенной функции lsolve, найдем решение системы и сравним с результатами вычислительной работы.

Тексты программ
Программа для вычисления матрицы в зависимости от размера m и заданного параметра c.
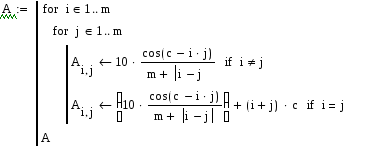
![]()
![]()
![]()
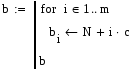
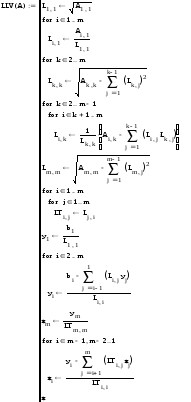
Программа
для вычисления решения системы с помощью
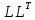 -разложения
-разложения
Вывод:
В
процессе работы была разработана
программа для вычисления системы
уравнений с помощью метода
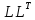 -разложения.
При
анализе результатов вычислительного
процесса была обнаружена погрешность,
но она
является достаточно малой, чтобы
утверждать, что программа работает
неверно. Также в ходе работы было
выяснено, что хоть метод
-разложения.
При
анализе результатов вычислительного
процесса была обнаружена погрешность,
но она
является достаточно малой, чтобы
утверждать, что программа работает
неверно. Также в ходе работы было
выяснено, что хоть метод
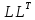 -разложения
и имеет ряд сходств с методом LU-разложения,
можно
видеть и отличия между двумя этими
методами. Так, например, не осуществляется
выбор ведущего элемента. Также вместо
двух матриц L
и U
мы получаем в результате только одну
матрицу, умножаемую на саму себя (из-за
чего это разложение иногда называют
квадратным корнем матрицы). Оба этих
свойства стали возможны за счет
положительной определенности и
симметричности матрицы. Ещё полезными
свойствами данного разложения является
то, что оно требует примерно в два раза
меньше операций, чем LU-разложение и
является гарантированно устойчивым.
-разложения
и имеет ряд сходств с методом LU-разложения,
можно
видеть и отличия между двумя этими
методами. Так, например, не осуществляется
выбор ведущего элемента. Также вместо
двух матриц L
и U
мы получаем в результате только одну
матрицу, умножаемую на саму себя (из-за
чего это разложение иногда называют
квадратным корнем матрицы). Оба этих
свойства стали возможны за счет
положительной определенности и
симметричности матрицы. Ещё полезными
свойствами данного разложения является
то, что оно требует примерно в два раза
меньше операций, чем LU-разложение и
является гарантированно устойчивым.
