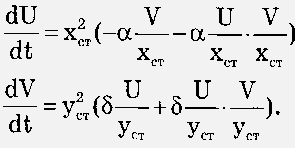Ответы на билеты по информатике МПФ / 19

Билет№19

1. База данных Access. Поиск данных при помощи запросов. Логические операции, используемые в запросах.

ACCESS- современная БД, вхлдящая в состав Microsoft office.

Запросы пишутся на языке SQL. Простой запрос имеет вид: Поле Отношение Значение.

Двойные кавычки указывают, что это - текстовая константа, а не, к примеру название другого поля.

В качестве знаков Отношения используют: =,<,>,<=,>=,<>.

Сложные(или составные) запросы состоят из простых запросов объединенных логическими операторами NOT(не),AND(и),OR(или).

Для обеспечения сохранности и целостности данных все требования на выборку, редактирования и ввода данных оформаляется в виде транзакций.

Транзакция-в информатике, группа последовательных операций, которая представляет союой логическую еденицу работу с данными. Для повышения скорости работы несколько транзакций могут работать параллельно. Если транзакция не завершилась успехом, то при следующем открытии базы обнаружиывается запись о незавершенной транзакции и выполняется “откат”-обратное преобразование данных по ненезавершенной транзакции с восстановлением последней работоспособной версии базы.

Запросы являются одним из основных инструментов выборки, обновления и обработки данных в таблицах базы данных. Запрос позволяет сформировать пользовательское представление о данных. Результат выполнения запроса — это новая, чаще всего временная, таблица, которая существует до закрытия запроса. Структура такой таблицы определяется выбранными из одной или нескольких таблиц полями. Записи формируются путем объединения записей таблиц, участвующих в запросе. Способ объединения записей различных таблиц указывается при определении их связи. Условия отбора, сформулированные в запросе, позволяют фильтровать записи, составляющие результат объединения таблиц. Простейшие запросы могут быть созданы с помощью мастера. Любой запрос можно создать в режиме конструктора. Конструктор предоставляет удобное для пользователя диалоговое графическое средство формирования запросов, с помощью которого легко может быть построен сложный запрос.

Запрос строится на основе одной или нескольких взаимосвязанных таблиц, позволяя объединять данные, содержащиеся в них. При этом могут использоваться таблицы базы данных, а также сохраненные таблицы, полученные в результате выполнения других запросов. Кроме того, запрос может строиться непосредственно на другом запросе с использованием его временной таблицы с результатами.

Запрос позволяет выбрать необходимые данные из одной или нескольких взаимосвязанных таблиц, произвести вычисления и получить результат в виде виртуальной таблицы. Полученная таблица может использоваться в качестве источника данных в формах, отчетах, страницах доступа к данным, других запросах. Через запрос можно производить обновление данных в  таблицах, добавление и удаление записей.

С помощью запроса можно выполнить следующие виды обработки данных:

- включить в результирующую таблицу запроса заданные пользователем поля;

- выбрать записи, удовлетворяющие условиям отбора;

- произвести вычисления в каждой из полученных записей;

- сгруппировать записи, которые имеют одинаковые значения в одном или нескольких полях, в одну запись и одновременно для других полей образовавшихся групп выполнить одну из статистических функций;

- произвести обновление полей в выбранном подмножестве записей;

- создать новую таблицу базы данных, используя данные из существующих таблиц;

- удалить выбранное подмножество записей из таблицы базы данных; "а добавить выбранное подмножество записей в другую таблицу.

Последовательное выполнение ряда запросов позволяет решать достаточно сложные задачи, не прибегая к программированию. В Access может быть создано несколько видов запроса:

- запрос на выборку — выбирает данные из взаимосвязанных таблиц и других запросов. Результатом является таблица, которая существует до закрытия запроса. На основе такого запроса могут строиться запросы других видов

- запрос на создание таблицы — также выбирает данные из взаимосвязанных таблиц и других запросов, но, в отличие от запроса на выборку, результат сохраняет в новой постоянной таблице.

- запросы на обновление, добавление, удаление — являются запросами действия, в результате выполнения которых изменяются данные в таблицах.

2 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМЫ ИЗ ДВУХ ВЗАИМОДЕЙСТВУЮЩИХ ПОПУЛЯЦИЙ. (МОДЕЛЬ "ХИЩНИК - ЖЕРТВА").

Допустим, что на некоторой территории обитают два вида животных: кролики (питающиеся растениями) и лисы (питающиеся кроликами). Пусть число кроликов , число лис . Используя модель Мальтуса с необходимыми поправками, учитывающими поедание кроликов лисами, приходим к следующей системе, носящей имя модели Лотки — Вольтерра:

Эта система имеет равновесное состояние, когда число кроликов и лис постоянно. Отклонение от этого состояния приводит к колебаниям численности кроликов и лис, аналогичным колебаниям гармонического осциллятора. Как и в случае гармонического осциллятора, это поведение не является структурно устойчивым: малое изменение модели (например, учитывающее ограниченность ресурсов, необходимых кроликам) может привести к качественному изменению поведения. Например, равновесное состояние может стать устойчивым, и колебания численности будут затухать. Возможна и противоположная ситуация, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов.

Это сложная система нелинейных дифференциальных урав­нений. Сначала найдем стационарное решение х = const, у = const, то есть dx/dt = 0, dy/dt == 0. Система дифференциальных уравнений при этом сводится к алгебраическим:

Рассмотрим решения:

Упростим систему уравнений, предполагая, что про­изошли малые отклонения численности хищников V(t) и жертв U(t) относительно стационарных значений:

У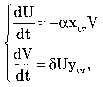читывая и пренебрегая членами второго порядка малости U/xст*V/xст и U/Yст*V/Yст, получим систему уравнений:

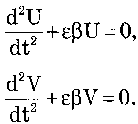,которую легко свести к дифференциальным уравнениям вто­рого порядка относительно переменных U и V:

Это характерные уравнения для описания гармонических ко­лебательных процессов. Решения уравнений Отношение амплитуд отклонений:

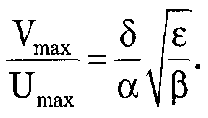
В результате численности особей при малых отклонениях от стационарных значений равны:

Таким образом, численности популяций х и у испытывают гар­монические колебания относительно стационарных значений с одинаковой частотой , но смещенные по фазе на фи0. Пери­одичность изменения численности хищников и жертв наблюдалась и на опыте.

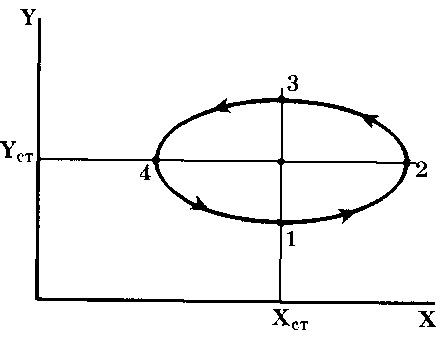
Допустим, произошло отклонение численности зайцев от ста­ционарного значения (1—>2). Если число зайцев возросло, то число рысей также увеличивается, но количество зайцев при этом постепенно начнет уменьшаться (точка 3). Это повлечет уменьшение числа рысей (точка 4), а следовательно увеличе­ние числа зайцев (точка 1). Модель «хищник-жертва» используется в настоящее время в медицине. Так при моделировании онкологических заболе­ваний опухолевые клетки рассматриваются как жертвы, а лим­фоциты, которые могут их подавлять, как хищники. В этом случае моделирование позволяет получить новые знания о про­цессах межклеточного взаимодействия при этих патологиях, находить пути оптимальной стратегии лечения, создавать но­вые средства борьбы с ними.

Моментом n-го порядка называется мат ожидание от n-ой степени случайной величины

Из определения следует, что первый момент совпадает с математическим ожиданием, второй – это средний квадрат, третий – средний куб и так далее

Центральным моментом n-го порядка случ величины называется n-ый момент случайной величины:

Первый центральный момент равен нулю. Второй – это средний квадрат отклонения от среднего. Он называется дисперсией и обозначается D. Третий центральный момент – это средний куб отклонения от среднего и и.д. Имеются формулы связывающие моменты и центральные моменты:

Дисперсия – средний квадрат отклонения от среднего, то есть имеет квадратичную размерность. Для роста она измеряется в м² для возраста – год² и т.д. Поэтому для анализа величины разброса используется не сама D, а квадратный корень из нее, кот называется среднеквадратичным отклонением: