Ответы на билеты по информатике МПФ / 2

Билет №2

1.Аналоговое и числовое кодирование. Единицы измерения объемов информации. Характерные объемы и информации и скорости их обработки. Информационная избыточность. Архивация и сжатие информации.

Существует два способа кодирования чисел для их записи – аналоговое и числовое.

При аналоговом кодировании число записывается одним сигналом, который может иметь любые промежуточные значения в диапазоне возможных значений, причем чем больше число, тем больше кодирующий его сигнал.

При числовом кодировании число записывается несколькими дискретными сигналами, который может иметь только одно из нескольких значений. Например, если время отображается на электрическом табло с набором лампочек, то каждая лампочка может либо гореть, либо нет.Единицы измерения информации служат для измерения объёма информации — величины, исчисляемой логарифмически. Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество информации — складывается. Чаще всего измерение информации касается объёма компьютерной памяти и объёма данных, передаваемых по цифровым каналам связи. Измеряются в: байт, килобайт, мегабайт, гигабайт. Избыточность информации — термин из теории информации, означающий превышение количества информации, используемой для передачи или хранения сообщения, над его информационной энтропией. Для уменьшения избыточности применяется сжатие данных без потерь, в то же время контрольная сумма применяется для внесения дополнительной избыточности в поток, что позволяет производить исправление ошибок при передаче информации по каналам, вносящим искажения (спутниковая трансляция, беспроводная передача и т. д.).

Архивация файла - это процесс преобразования информации, хранящейся в файле, к виду, при котором уменьшается избыточность в ее представлении и соответственно требуется меньший объем памяти для хранения. При этом имеется возможность закрыть доступ к упакованной в архив информации паролем. Сжатие информации в файлах производится за счет устранения избыточности различными способами, например за счет упрощения кодов, исключения из них постоянных битов или представления повторяющихся символов или повторяющейся последовательности символов в виде коэффициента повторения и соответствующих символов.

2. Распределение Бернулли, биномиальное распределение, распределение Пуассона. Определение и свойства.

Распределение Бернулли. Случайная величина, которая с вероятностью р равна единице с вероятностью q = 1- p равна 0.

Ее математическое ожидание (или среднее арифметическое) равно р , а дисперсия ( квадратный корень из дисперсии называется среднеквадратичным отклонением и служит мерой разброса случайной величины) равна р*q = p*(1-p).

Распределение Бернулли возникает при рассмотрении случайных событий, которые произойдут (единица) или не произойдут (ноль).

Это распределение однопараметрическое, т. е. точное распределение конкретной случайной величины задается одним параметром р (равным математическому ожиданию, или среднему).

Биномиальное распределение. Пусть 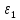, ,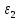…- независимые случайные величины. распределенные по Бернулли с одним и тем же р. Пусть случайная величина ŋ=+ +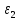…. Тогда ŋраспределена биномиально с параметрами (р;N).

Ее математическое ожидание равно р*N. Вероятность того, что ŋ= n, где n=1,2,3,…N, равна Р(n)=(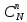 /N!)*, где 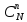-количество сочетаний из N по n, называемое также биномиальным распределением, а N!=1*2*3*…..*N – факториал.

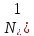Биномиальные случайные величины – двухпараметрическое семейство. У биномиальной случайной величины математическое ожидание равно р*N и дисперсия – р*(1-р)*N . Если две независимые случайные величины распределены биномиально с показателями (р,) и (р,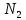) соответственно, то их сумма распределена биномиально с показателями (р, + 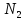). (Если р у них различны, то сумма - не биномиальная величина)

Распределение Пуассона. Это распределение получается из биномиального в том случае, когда очень мало, а Nочень велико, т.е. случайная величина является суммой большого количества маловероятных событий. Это однопараметрическая случайная величина, задаваемая своим математическим ожиданием ʎ. Для нее имеем следующее распределение вероятности: Р(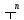n)=(/n!)*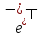. В отличие от биномиального распределения, для распределения Пуассона не обязательно, чтобы вероятности наступления события были одинаковы, достаточно, чтобы они были малы. У пуассоновой случайной величины дисперсия равна математическому ожиданию. Сумма двух независимых пуассоновых случайных величин с математическими ожиданиями и есть пуассонова случайная величина с математическим ожиданием +.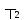