sintez_4P

Последовательность синтеза реактивного ЧП

1. Осуществляют общую проверку на реализуемость ПФ -ЧП: условие Фиалкова выполняется (коэффициенты ПФ ЧП положительны, причем коэффициенты числителя при одинаковых степенях аргумента не превышают соответствующих коэффициентов знаменателя); в режимах его КЗ или ХХ нули и полюсы ПФ мнимые, причем полюсы простые, а при нормированной нагрузке должны быть мнимые нули.

2. Производят определение параметров синтезируемого -ЧП. В режимах КЗ или ХХ ЧП ПФ имеет вид или , причем и – это полиномы четных степеней и для определения параметров ЧП делят числитель и знаменатель ПФ на произвольный нечетный полином , корни которого мнимые, простые и чередуются с корнями 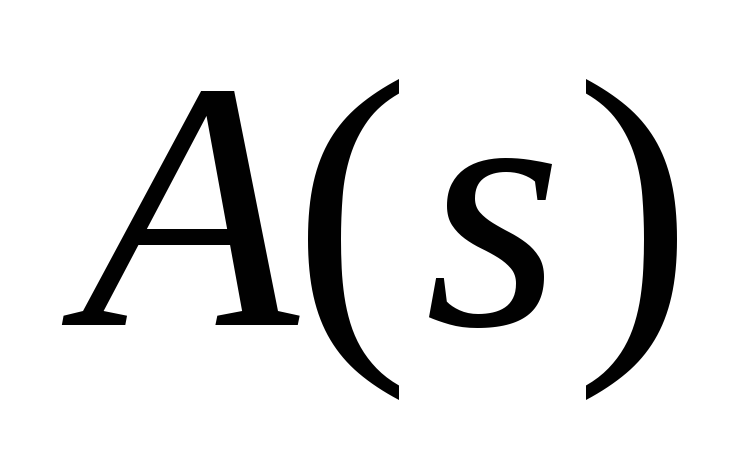, т.е. , или , 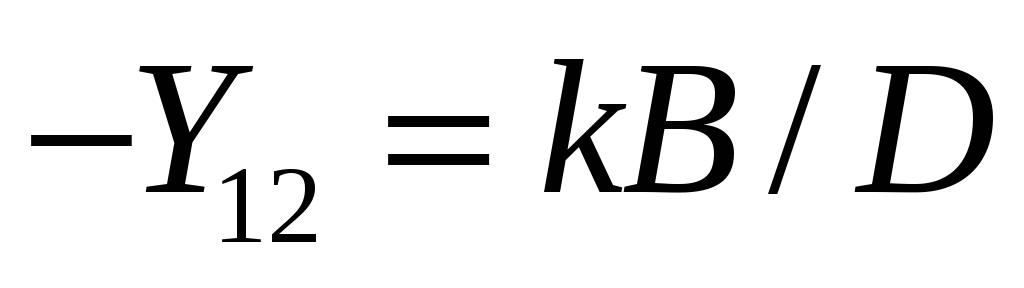. Сразу же проверяют найденные или на соответствие основному свойству . может быть дробно-рациональной функцией. При нормированной нагрузке ПФ имеет вид или . Разбиваем полином знаменателя на две части , где – полиномы четных и нечетных степеней . Если – полином четных степеней , то и числитель и знаменатель делят на , получая , откуда (или аналогично и ). Если – полином нечетных степеней , то делят на , получая , т.е. , а 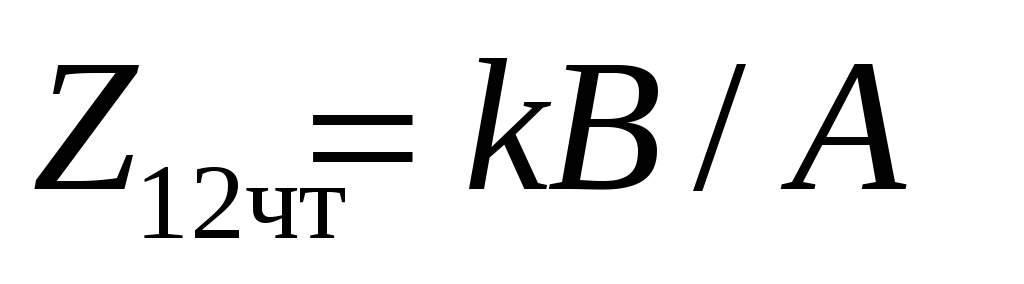(или аналогично и ). 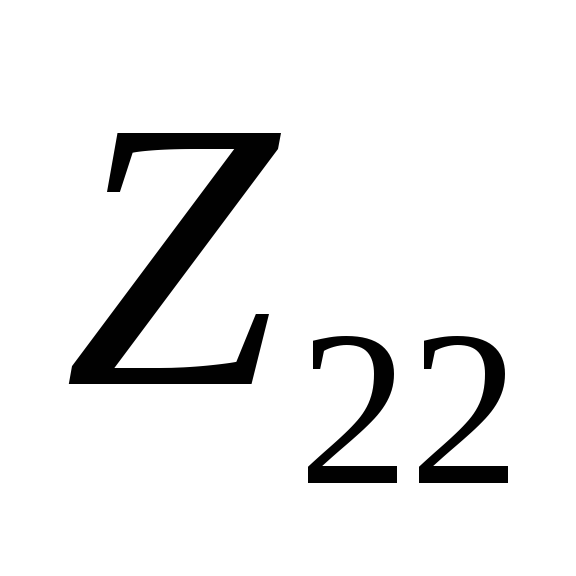Сразу же проверяют найденные или на выполнение основного свойства . Если эта проверка не выполняется, реализовать заданную ПФ в виде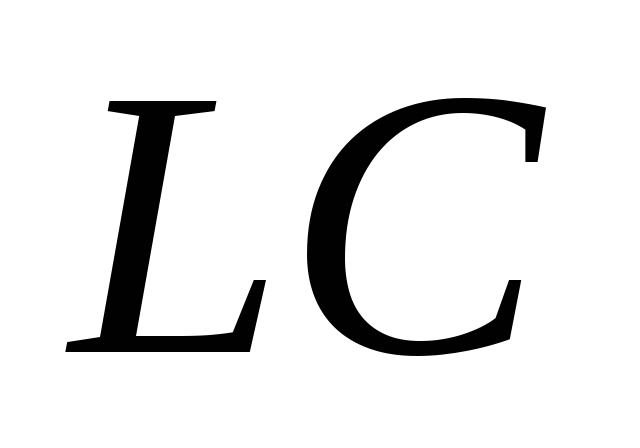-ЧП невозможно. Кроме того проверяют найденные (или ) на условие Фиалкова.

3. Записывают нули ПФ ЧП на основании найденных параметров: это частные полюсы 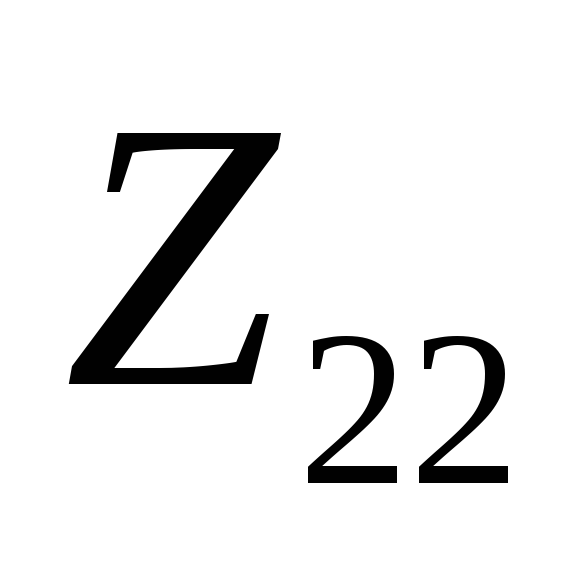(или ) и нули или (). Переходят к реализации ЧП, помня, что 1) нули ПФ ЧП можно синтезировать только полюсами или ; 2) синтезировать ЧП умеем только выделением полюсов ДП или их остатков.

4. Синтезируют частные полюсы (или ) (нули I категории в ПФ ЧП) в виде продольного сопротивления (или поперечной проводимости ).

5. Рекомендуется синтезировать нули ПФ ЧП, которые совпадают с нулями остатков от реализации (или ) (II категорию нулей ПФ), путем полного выделения полюсов обращенных остатков в виде продольных сопротивлений (или поперечных проводимостей ).

6. Рекомендуется синтезировать нули, которые не совпадают с корнями остатков от реализации или 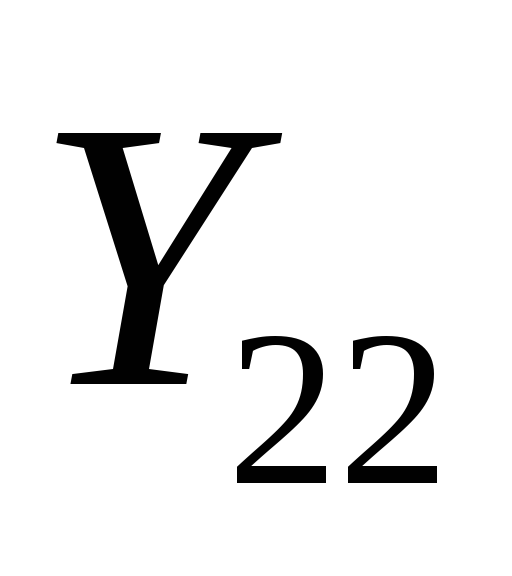(III категорию нулей ПФ). Методом «проб» пытаются частично выделить какой-либо полюс остатка от реализации (или ) обращенного остатка так, чтобы в новом остатке был нуль, совпадающий с еще не реализованным нулем III категории. Если первая попытка неудачна, пытаются частично выделить другой полюс (обычно из ближайших полюсов к нулю III категории) и т.д. Если выполнено (условие правильного частичного выделения), где – коэффициент при полном выделении полюса, 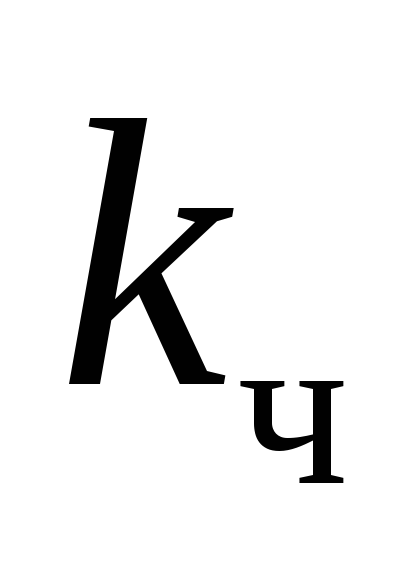– полученный частичный коэффициент, то остаток обращается, и искомый нуль III категории реализуется как полностью выделенный полюс в виде поперечной проводимости (или продольного сопротивления ) ЧП.

7. Проверяют, что синтез закончен правильно (если реализацию проводили по , то последним элементом синтеза (Первым со стороны 1-1) должна быть поперечная проводимость ; если синтезировали , последним элементом должно быть продольное сопротивление )

Если синтез закончен неверно, то на какой-то стадии процедуру синтеза надо изменить. Например, поменять местами 5 и 6 пункты.

8. Проверяют ПФ и определяют .

Последовательность синтеза -ЧП

1. Осуществляют общую проверку на реализуемость ПФ -ЧП: условие Фиалкова выполняется (коэффициенты ПФ ЧП положительны, причем коэффициенты числителя при одинаковых степенях аргумента не превышают соответствующих коэффициентов знаменателя); нули и полюсы отрицательные, полюсы простые.

2. Производят определение параметров синтезируемого -ЧП. В режимах КЗ или ХХ ЧП ПФ имеет вид или , для определения параметров ЧП делят числитель и знаменатель ПФ на произвольный полином такой, что корни простые, отрицательные и чередуются с корнями , чтобы получившиеся и удовлетворяли основному свойству (нули и полюсы отрицательные, простые, чередуются и ближайшим к началу координат у 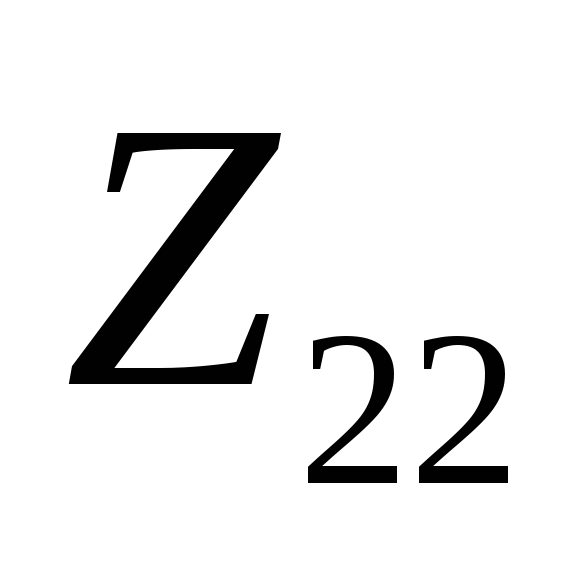должен быть полюс, а у – нуль). 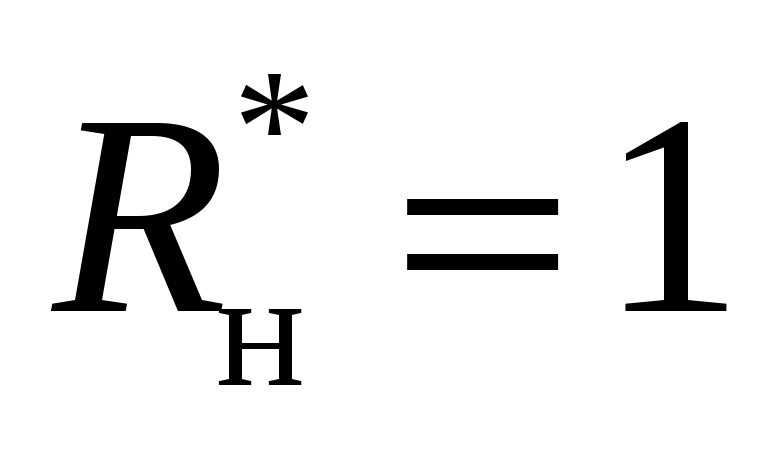При нормированной нагрузке ПФ имеет вид или . Полином знаменателя раскладывают на сумму двух полиномов с положительными коэффициентами, причем корни полинома выбирают отрицательными, лежащими правее корней . Тогда корни полинома будут автоматически левее корней , т.е. корни полиномов и простые, отрицательные, чередуются и ближайшим к началу координат будет корень у . При определении -параметров ЧП делят числитель и знаменатель ПФ на, а при определении -параметров – на , так что , или , . В результате и удовлетворяют основному свойству , т.е. у ближайшим к началу координат является полюс, а у 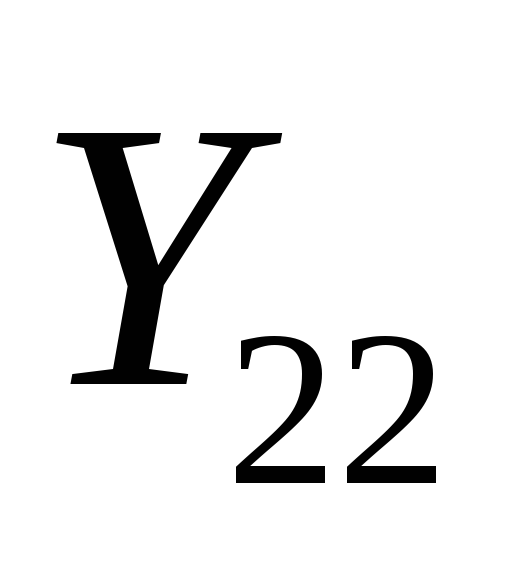– нуль. Проверяют: 1) (или ) на , 2) (или ) на условие Фиалкова.

3. Переходят к параметрам соответствующего -ЧП по формулам при , или при , .

4. Реализуют схему цепи в соответствии с общей последовательностью синтеза -ЧП

5. Проверяют, что синтез закончен правильно (если реализацию проводили по , то последним элементом синтеза (Первым со стороны 1-1) должна быть поперечная проводимость ; если синтезировали , последним элементом должно быть продольное сопротивление ).

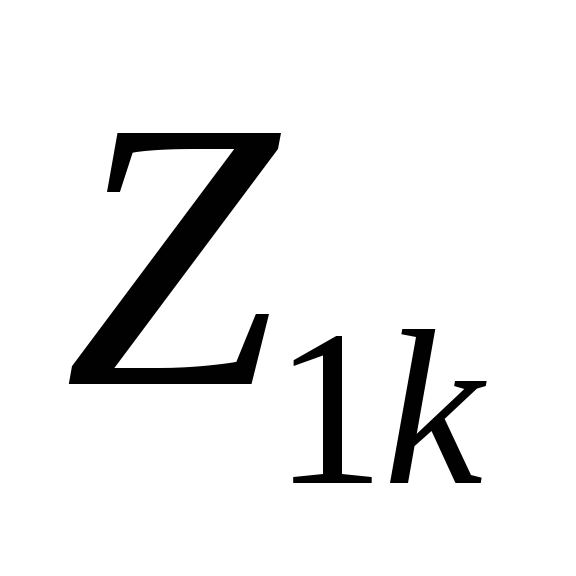Если синтез закончен неверно, то на какой-то стадии процедуру синтеза надо изменить. Например, поменять местами пункты в реализации -ЧП.

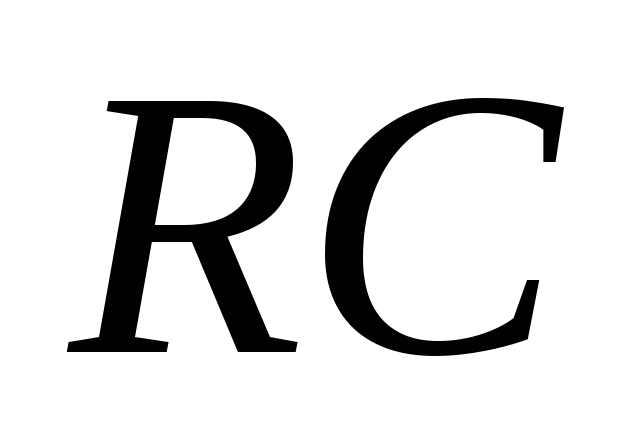6. Заменой на получают искомый -ЧП

7. Проверяют ПФ и определяют .