
uch_posobie_2014_ver_11
.pdf
( а − Uвыx)/R0 = (Uвx1 − а)/R1 + (Uвx2 − а)/R2 + (Uвx3 − а)/R3.
В силу соединения неинвертирующего входа ОУ с «землей» ( + = 0) и
допущения о КОУ а 0, откуда
−Uвыx/R0 = Uвx1/R1 + Uвx2/R2 + Uвx3/R3,
т. е.
Uвыx = −(Uвx1R0/R1 + Uвx2R0/R2 + Uвx3R0/R3).
Отношения R0/Ri выполняют роль коэффициентов передачи для сиг-
налов Uвxi, их можно обозначить через KUi = R0/Ri. Тогда, в общем виде,
Uвыx = −Σ Uвx i KUi. Эта формула верна при любом количестве слагаемых. Таким образом, выходной сигнал равен сумме входных с учетом мас-
штабирующих коэффициентов и с обратным знаком. Данная схема называется инвертирующим сумматором. Отметим, что при сложении сигналов «без весов» следует все входные сопротивления брать одинаковыми (например,
R0 = Ri). При сложении «с весами» следует обеспечить соотношение значе-
ний сопротивлений Ri, обратное соотношению «весов» (т. е. КUi).
6.6. Активная дифференцирующая цепь
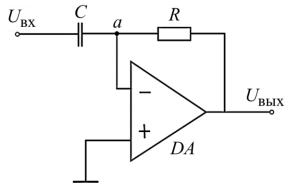
Рассмотрим схему, представленную на рис. 6.18. Докажем, что эта цепь является дифференцирующей. Итак, Zвx = – jXC = – j/(2 fC), ZOC = R.
Тогда выражение для коэффициента передачи имеет вид
KU = – R/(–j/(2 fC)) = – j2 fCR.
При f = 0 КU = 0, при f |KU| , а реально ограничивается собственным коэффициентом усиления операционного усилителя KОУ. Таким образом, схема, представленная на рис. 6.18, является фильтром высоких частот, т. е. во временной области – дифференцирующей цепью. Более строгое доказательство того, что выходной сигнал схемы есть производная от входного сигнала, также производится на основе допущений о свойствах ОУ (КОУ ,
Rвx ОУ ). Уравнение токов для точки а имеет вид I1 = I2 + Iвx ОУ или, по-
скольку Iвx ОУ 0, I1 = I2, т. е. CdUC/dt = UR/R.
71
С учетом а 0: UC
Рис. 6.18
= Uвx – а = Uвx, UR = а – Uвыx = –Uвыx.
Подставив эти значения, полу-
чим: CdUвыx/dt = Uвыx/R, Uвыx = = –CRdUвx/dt, что и требовалось доказать. В отличие от дифференцирующей цепи, состоящей только из элементов R и С и называемой пассивной (см. 3.1), данная схема именуется активной дифференцирующей цепью, так как содержит активный
элемент (ОУ).
Активные интегрирующая и дифференцирующая цепи отличаются от своих пассивных аналогов не только схемотехнически (т. е. составами элементов), но и количественными значениями коэффициентов передачи. Если у обеих пассивных цепей коэффициенты передачи не превосходят единицу, то у активных дифференцирующих и интегрирующих цепей они могут быть весьма значительными. Это крупное преимущество активных интегрирующих и дифференцирующих цепей, где наряду с преобразованием сигнала по форме (т. е. по спектру) достижимо и увеличение его по амплитуде.
Реально К ОУ при больших частотах снижается из-за наличия паразит-
ных емкостей, в силу чего снижается и |K U | схемы (см. рис. 6.4), т. е. активный фильтр высоких частот, построенный на реальном ОУ, фактически является полосовым фильтром.
6.7. Активная интегрирующая цепь
Допустим, что входным сопротивлением Zвx в схеме является сопротивление R, а в качестве обратной связи служит емкость С. Такая схема приведена на рис. 6.19. Как видно из сравнения схемы рис. 6.19 с активной дифференцирующей схемой, приведенной на рис. 6.18, она отличается тем, что R и С в ней поменялись местами (между прочим, пассивные интегрирующая и дифференцирующая цепи в своем простейшем варианте также различаются тем, что в них элемен-
ты R и С меняются местами). Подставим в качестве Zвx и ZOC их конкретные
72

значения: Zвx = R, ZOC = – jXC = – j/(2 fCR), где f – частота сигнала. Тогда
KU = + j/(2 fCR).
При f 0 |KU| ; в реальных условиях невозможно получить с по-
мощью дополнительных элементов, подключаемых к ОУ, |КU| >КОУ. При f |KU| 0. Схема, представленная на рис. 6.19, является фильтром низких частот. Во временной области фильтру низких частот соответствует интегрирующая цепь.
Тот факт, что схема (рис. 6.19) является интегрирующей, может быть доказан и более строго, хотя и сложнее. Воспользуемся уже известными
(см. 6.2) допущениями относительно ОУ: KОУ , R вx ОУ . Кроме того,
запишем соотношение между током через емкость IС и напряжением на емкости
UС IС(t) = CdUC(t)/dt. Тогда, повторяя вывод для инвертирующего усилителя, запишем уравнение токов для точки a:
I1 = I2 + Iвx ОУ; принимая Iвx ОУ = 0 (в силу Rвx ОУ ), а также с учетом I2 = IC, получаем: I1 = CdUC(t)/dt; но
I1 = IR = (Uвx – а)/R, UC = а – Uвыx.
Поскольку а 0 (см. 6.2), то запи-
шем соотношение Uвx/R = –CdUвыx/dt. Интегрируя, получим следующее вы-
ражение для выходного сигнала: Uвыx = –1/(RC) Uвxdt.
Таким образом, выходной сигнал схемы (рис. 6.19) является интегралом от входного, и схема действительно может быть названа интегрирующей. В отличие от интегрирующей цепи, состоящей только из элементов R и С и называемой пассивной, данная схема именуется активной интегрирующей цепью. Если на вход схемы подать меандр (рис. 6.20, а), то на выходе получается последовательность равнобедренных треугольных импульсов (рис. 6.20, б) или трапецеидальных импульсов (рис. 6.20, в) – в зависимости от соотношения амплитуды импульсов и питания ОУ. Несмотря на важность
строгого вывода соотношения, связывающего Uвыx с Uвx, бóльшую ценность
73

для дальнейшего рассмотрения имеет первый способ доказательства. Отме-
тим, что формула KU = – ZOC/Zвx является универсальной; если и в обратной связи, и во входной цепи включены частотно-независимые элементы (например, сопротивления), то и КU есть величина постоянная, не зависящая от f, а схема выполняет лишь функцию изменения амплитуды сигнала; если один из элементов (или оба) – частотно-зависимый, то KU = KU (f) и схема представ-
ляет собой фильтр. Если ZOC и (или) Zвx – какие-либо нелинейные элементы (например, диоды), то схема становится нелинейным преобразователем, а если представляют собой сопротивления, зависимые от управляющего воздействия (например, транзисторы), то получается параметрическая схема.
Активные интегрирующие и дифференцирующие цепи отличаются от своих пассивных аналогов не только схемотехнически (т. е. составами элементов), но и количественными значениями коэффициентов передачи. Если у обеих пассивных цепей коэффициенты передачи не превосходят единицу, то у активных дифференцирующих и интегрирующих цепей они могут быть весьма значительными. Это крупное преимущество активных интегрирующих и дифференцирующих цепей, наряду с преобразованием сигнала по форме (т. е. по спектру) достижимо и увеличение его по амплитуде.
Как указывалось, схемы, представленные на рис. 6.18 и 6.19, являются простейшими фильтрами – низких и высоких частот соответственно. В отличие от фильтров, состоящих из пассивных элементов (R, L, С) и именуемых пассивными, фильтры, содержащие активный элемент (в частности, операционный усилитель), называют активными.
74
Кроме того, активные ДЦ и ИЦ отличаются от своих пассивных аналогов полярностью выходных сигналов: это объясняется тем, что в активных фильтрах использовано инвертирующее включение ОУ.
Активные ДЦ используют для укорочения импульсов, в цепях запуска ждущих схем (см. 10.1) и т. д. Следует помнить, что первым на выходе активной ДЦ появляется «обратный выброс», т. е. короткий импульс, имеющий полярность, противоположную входному сигналу.
Активные ИЦ применяют для формирования импульсов треугольной формы: чаще – равнобедренных, реже – пилообразных (о формировании пилообразных импульсов см. 10.10).
6.8. Логарифмический преобразователь
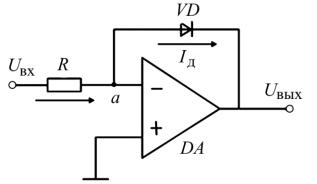
Нелинейными функциональными преобразователями сигналов называют электронные схемы, выходные сигналы которых являются нелинейными функциями входных. Логарифмические преобразователи (иногда их называют логарифмическими усилителями, что неверно, так как логарифмирование – процесс нелинейный, а усиление – линейный) получают посредством включения в цепь обратной связи ОУ нелинейного элемента, сопротивление которого меняется при изменении приложенного к нему напряжения. В качестве такого элемента обычно используют диод (рис. 6.21) или транзистор.
При этом достаточную для практики точность обеспечивает аппроксимация вольт-амперной характеристики p–n-перехода логарифмической функцией (на самом деле зависимость тока через открытый диод представляет собой дробно-степенную функцию). Так,
для всех трех указанных схем мож- Рис. 6.21 но записать:
Uвыx = –Uн. э = –N lg (Iвx/ I0) = –N lg (Uвx/ I0R1) =
= –N lg (Uвx) + N lg (I0R1) = –N lg (Uвx),
где Uвx – напряжение на входе схемы; Uвыx – выходное напряжение схемы;
75

Uн.э – напряжение на нелинейном элементе (диоде или транзисторе); Iвx – входной ток схемы (и одновременно, в силу огромного значения входного сопротивления ОУ, ток через нелинейный элемент); I0 – обратный ток диода или ток неосновных носителей p–n-перехода «эмиттер – база» транзистора; N – масштабный коэффициент; значение R1 подбирают таким, чтобы выпол-
нялось равенство I0R1 = 1 В. Диодная схема (рис. 6.21) обладает большим динамическим диапазоном входных напряжений (до 7 декад), однако она может работать только с однополярным входным сигналом. Транзисторная схема работает с разнополярными входными сигналами, однако точность логарифмирования при ее использовании ниже, чем при использовании диодной схемы, и динамический диапазон меньше (4…6 декад). Наличие транзистора в обратной связи ОУ способствует повышению склонности схемы к самовозбуждению. В качестве противодействия такому нежелательному явлению в цепь эмиттера транзистора включают сопротивление. Схема логарифмического преобразователя является инвертирующей, так как входное напряжение подается на инвертирующий вход ОУ.
На ином принципе построена схема логарифмического преобразователя с кусочно-линейной аппроксимацией (КЛА) амплитудной характеристики (рис. 6.22). Получение КЛА логаримической зависимости с помощью схемы,
Рис. 6.22 |
|
Рис. 6.23 |
76

представленной на рис. 6.22, поясняют графики на рис. 6.23.
В схеме, изображенной на рис. 6.22, не используется какая-либо нелинейность и логарифмическая зависимость заменяется кусочной аппроксимацией с помощью ломаной линии.
Фактически схема представляет собой линейный инвертирующий усилитель на ОУ, у которого коэффициент усиления КU зависит от уровня входного сигнала. Входной сигнал сравнивается с многочисленными порогами, формируемыми резистивным делителем. Если порог превышен, то открывается диод, включенный в цепь обратной связи усилителя, и эта цепь начинает
влиять на значение КU = − ROC/Rвx.
Сопротивления R во всех цепях обратной связи одинаковы. Если превышен только самый нижний порог, то включена одна цепь обратной связи,
ROC = R, КU = −R/Rвx; при превышении второго порога появляется вторая цепь, параллельная первой и ROC = R/2, КU = −R/2Rвx (в два раза меньше,
чем при самом малом входном сигнале), далее ROC по мере превышения все новых порогов принимает значения ROC = R/3, ROC = R/4 и т. д., а КU, соответственно, снижается в 3, 4 раза и т. д.
6.9. Антилогарифмический преобразователь
Антилогарифмирование и логарифмирование являются взаимно обратными функциями. Поэтому очевидно, что в антилогарифмическом усилителе нелинейный элемент включен на входе ОУ, а в обратной связи установлено
активное сопротивление R1. Схема усилителя приведена на рис. 6.24. Для этой схемы можно записать: Uвыx = –R I0 anti lgUвx. При больших значени-
Рис. 6.24 |
Рис. 6.25 |
77
ях Uвx выходное напряжение приближается по уровню к напряжению источника питания ОУ –Е (рис. 6.25) и перестает изменяться; антилогарифмическая зависимость нарушается. Схема, изображенная на рис. 6.24, обеспечивает антилогарифмирование (потенцирование) однополярных сигналов. При необходимости получения логарифмических и антилогарифмических зависимостей повышенной точности применяют схемы с кусочно-линейной аппроксимацией амплитудной характеристики с использованием диодных матриц.
7. КОМПАРАТОРЫ
Компараторами называют схемы сравнения двух напряжений (раньше слово «компаратор» не применялось, использовался термин «схема сравнения»). Результат сравнения – дискретный: важен сам факт того, что один сигнал больше другого, а насколько больше – несущественно.
Чаще всего компараторы создают на базе ОУ – в этом случае легко можно получить передаточную характеристику с практически вертикальным участком (см. рис. 7.3). Для этого надо иметь очень большой коэффициент усиления, равный отношению сопротивления в обратной связи к входному
сопротивлению; проще всего разомкнуть обратную связь (R OC ) . Отсутствие обратной связи характерно практически для всех схем компараторов. Сигналы на выходе компараторов принимают значения ±Е (где Е – напряжения источников питания ОУ).
Различают двухвходовые, одновходовые и регенеративные компараторы. Особое положение занимает нуль-детектор (второе, более редко употребляющееся название – нуль-компаратор).
7.1. Двухвходовый компаратор
Двухвходовый компаратор предназначен для сравнения двух сигналов одинаковой полярности. Его схема изображена на рис. 7.1. Поясняющий график (диаграмма напряжений на обоих входах и выходе компаратора) приведена рис. 7.2.
Для подачи сигналов используются оба входа ОУ, обратной связи нет. Выходной сигнал принимает значения ±Е, которые меняются скачком. Если сигнал на неинвертирующем входе превосходит сигнал на инвертирующем входе, то выходной сигнал равен +Е, в противном случае –Е.
78

Рис. 7.1 |
Рис. 7.2 |
Сплошная линия на графике (рис. 7.2) соответствует идеальному компаратору. Реальные компараторы мгновенно переключиться не могут, в силу ряда причин:
– при переключении компаратора транзисторы в составе ОУ переходят из глубокого насыщения в глубокую отсечку и наоборот, при этом нужно время, чтобы рассосались избыточные носители заряда;
–коэффициент усиления реального ОУ конечен, поэтому ПХ ОУ содержит не вертикальный, а наклонный участок;
–на высоких частотах снижается крутизна S транзисторов в составе ОУ, в результате чего также уменьшается коэффициент усиления ОУ;
–из-за наличия паразитных емкостей импульсные сигналы приобретают фронты.
7.2. Одновходовый компаратор
Одновходовый компаратор предназначен для сравнения двух сигналов противоположной полярности по модулю. Его схема изображена на рис. 7.3. Поясняющий график приведен на рис. 7.4.
Для подачи обоих сигналов используется инвертирующий вход ОУ (сигналы поступают на вход ОУ через делитель, состоящий обычно из оди-
наковых сопротивлений; в результате напряжение UBX- = (Uвx1 + Uвx2) / 2), обратной связи нет.
Выходной сигнал принимает значения ±Е, которые меняются скачко-
образно в моменты, когда меняется знак UBX- . Очевидно, что смена знака
UBX- возможна только при разных знаках Uвx1 и Uвx2.
79

Рис. 7.3 |
Рис. 7.4 |
Разумеется, реальный одновходовый компаратор отличается по своим свойствам от идеального точно так же, как различаются идеальный и реальный двухвходовые компараторы. На нижнем графике (рис. 7.4) сплошной линией показана зависимость выходного сигнала идеального компаратора, штриховой линией – на выходе реального компаратора.
7.3. Регенеративный компаратор
Регенеративный компаратор обеспечивает сравнение входного сигнала с долей выходного. Эта схема редко применяется сама по себе, но зато является необходимой частью мультивибраторов (на ОУ) – генераторов прямоугольных импульсов. Схема изображена на рис. 7.5.
Принцип действия регенеративного компаратора поясняет рис. 7.6. Как и в других компараторах, в ней отсутствует обратная связь между выходом и
Рис. 7.5 |
Рис. 7.6 |
80
