Свойства несобственных интегралов 1го рода.

4. Если для любого , асходится, то сходится и несобственный интеграли при этом справедливо неравенствот. е. неравенство для функции можно интегрировать в смысле несобственного интеграла первого рода.

5. Если для любого а интегралрасходится, то расходится и интеграл от.Замечание: Свойства (1) и (2) позволяют делать оценки на несобственные интегралы первого рода, либо сверху либо снизу (первое свойство – сверху, второе свойство – снизу).

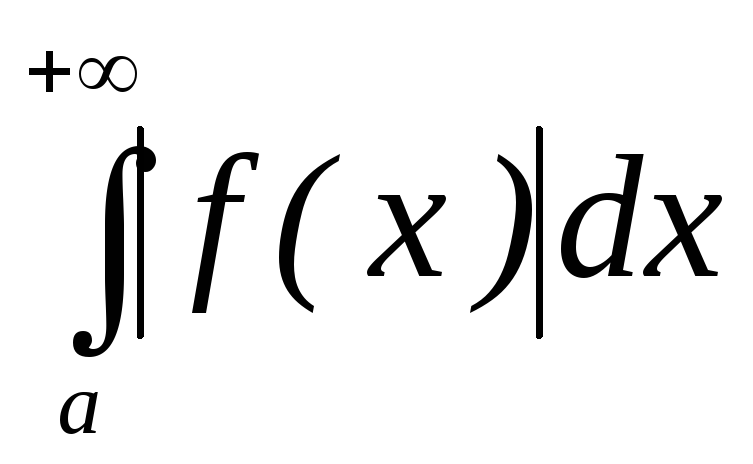6. Если сходится то сходится и интеграли при этом называется абсолютно сходящимся.Замечание: , Если же интегралрасходится, а интегралсходится то он называется условно сходящимся.Замечание: Из выше приведенных утверждений следует что из расходимости не следует расходимость: он может быть как сходящимся, так и расходящимся. Свойства(1), (2) и (3) формулируются аналогично и для других несобственных интегралов первого рода с другими приделами.

Комплексные числа (26).

Натуральные числа N: 0,1,2,3,… Целые числа: 0,

Рациональные числа: 1/2,1/3, 3/5 Иррациональные числа: и т. д.

Все это действительные числа. Обобщением действительных чисел являются комплексные числа z=x+iy где x-действительная часть комплексного числа R_eZ,

y- мнимая часть комплексного числа I_mZ, i- мнимая единица i²=-1

Z=x+iy=R_eZ+iI_mZ (), Z=x+iy называется алгебраической формой записи числа. Если I_mZ=0, то Z=x – действительное число. Если R_eZ=0, то Z=iy – число мнимое комплексные число. Если R_eZ= I_mZ=0, то Z=0

Два комплексных числа Z₁=x₁+iy₁, и Z₂=x₂+iy₂ называются равными если R_eZ₁=R_eZ₂ (x₁=x₂) и I_mZ₁= I_mZ₂ (y₁=y₂). Комплексное число Z=x+iy и называются комплексно сопряженными.

Геометрический смысл комплексных чисел:

РассмотримZ=x+iy. Каждому Z ставится в соответствии точка M(x,y) на комплексной плоскости Z и наоборот.

Ось OX (абсцисс) называется действительной осью, а ось OY (ординат) называется мнимой осью.

Рассмотрим вектор: Любому векторуи преобразуем. Возьмем полярную систему координатточкаM(x,y) , g – называется модулем комплексного числа, а - аргументом числаZ (). и определены неоднозначно а с точностью до числа кратного . Используя формулу(1) получим тригонометрическую форму записи комплексного числа . Используя формулу Эллера получим:,- действительные числа.Рассмотрим частные случаи:

Если - действительные числа. Если,,. В общем случаи: Модуль комплексного числа,argZ находится из уравнения

Пример:

R_eZ=1

I_mZ=-1

Замечание: Комплексно сопряженные числа Z=x+iy и геометрически изображаются двумя точками на комплексной плоскости зеркально симметричны относительно действительной оси(R_eZ). В показательной форме , то.

Действия над комплексными числами (27).

1. Сложение: Суммой двух комплексных чисел Z₁=x₁+iy₁ и Z₂=x₂+iy₂ называется Z=Z₁+Z₂=(x₁+x₂)+i(y₁+y₂). 2. Вычитание: Разностью двух комплексных чисел Z₁=x₁+iy₁ и Z₂=x₂+iy₂ называется Z которое будучи сложенным с Z₂ дает Z₁ Z=Z₁+Z₂=>Z₁=Z₂+Z=(x₁-_{_}x₂)+i(y1-y2), при сложении и вычитании комплексных чисел они должны быть представлены в алгебраической форме.