Интегрирование некоторых иррациональных функций интегралы от квадратичных иррациональностей (10)
Интегралы
вида:
,
гдеR-
рациональная дробь по
и
.
Здесь
производим
замену (
):
а).
a>0
и D>0
т. е.
не имеет действительных корней, тогда:
рационализируются т. е. сводится к
интегралу от рациональной дроби
подстановкой
:
т.
е. рационализируются.
б.
a>0
и D<0
т. е.
имеет действительные корни. В этом
случае
и рационализируются интеграл подстановкой
т.
е. рационализируется.
в.
a<0
и D>0
тогда at2+D=α2-t2
рационализируются подстановкой: t=αcosZ
и t=αsinZ
т. е. рационализируется.
Замечание: Кроме указанных тригонометрических подстановок могут использоваться и другие подстановки, а именно гиперболические.
а.
a>0
и D>0
Используем подстановку
получаем:
(т.
к.
)
б.
a>0
и D<0
Используем подстановку
получаем:
.
В этом случае лучше всего делать
тригонометрические подстановки:
t=αcosZ
и t=αsinZ
Замечание
№ 2: Кроме
тригонометрических подстановок
используют:
используют подстановки Эллера (1,2,3
подстановки).
1
подстановка Эллера: Если
a>0,
то делают подстановку
2
подстановка Эллера: c>0,
тогда
3
подстановка Эллера: Если
имеет действительные корни α и β то
делают подстановку
или
и находятx
и dx.
Замечание № 3: Существуют и другие классы интегралов от рациональных функций которые не всегда рационализируется а выражение в виде специальных функций к ним относятся эллиптические интегралы.
Определенный интеграл и его свойства (11)
Пусть
функция f(x)
определена и непрерывна на [a,b]
разобьем
отрезок [a,b]
точками x0=a,
x1
…, xn=b
на n
частичных отрезков [xi-1,
xi],
i=1,…,n,
обозначим через
длинна отрезка на каждом отрезков[xi-1,
xi]
выберем произвольно
составим сумму
и назовем интегральной суммой для
функцииf(x)
на [a,b].
Площадь
этой ступенчатой фигуры равна
.
Так какf(x)-непрерывная
функция на отрезке [a,b]
то она и ограничена на [a,b]
следовательно она ограничена и на
каждом отрезке [xi-1,
xi]
т.е. существует mi,
Mi,
что
дляi=1,…,
n
следовательно
при
>0,
а следовательно
(
нижняя
интегральная сумма,
верхняя
интегральная сумма).Опр.
Если существует предел интегральных
сумм
,
когда
то этот предел называется определенным
интегралом от функцииf(x)
на отрезке [a,b]
и образует
.
Итак
по определению
и этот предел не зависит как от способа
разбиения отрезка[a,b]
точкой xi
на частичные отрезки [xi-1,
xi],
так и от выбора точек
в них.
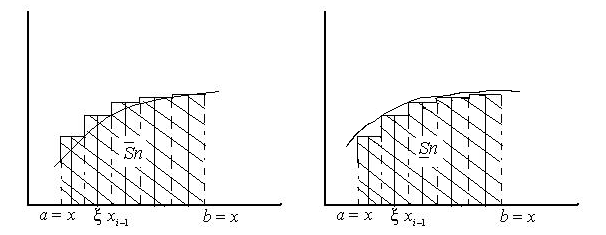
частные
случаи интегральной суммы
.
Численно при
на[a,b]
равен площади криволинейной трапеции
ограниченной снизу осью абсцисс, сверху
кривойf(x)
с право кривой x=b,
слева кривой x=b.
Геометрический смысл определенного интеграла – площадь кривой трапеции.
Свойства определенного интеграла.
1.
2.
3.
4.
5.
при условии
что интегралы существуют. 6.
Если
для любого
то и
7.
Если f(x)
непрерывна на [a,b],
то
(следует из непрерывности функции).
7. Свойство аддитивности:
Для любых чисел a,b,c
при
условии, что эти
существуют.
(т.е.
– непрерывна на каждом из отрезков).
Действительноно, если а<c<b, то из определения определенного интеграла
a<b<c
Аналогично c<a<b