Первообразная. Неопределённый интеграл и его свойства (1).

Опр. Первообразной для функциина интерваленазывают функцию, дифференцируемую наи удовлетворяющую условию. Отсюда следует, что функция,также является первообразной для функциина, т.к.

Опр. Совокупность первообразных для данной функции наназывают неопределенный интеграл и обозначают.

называется подынтегральным выражением, -подынтегральной функцией. По определению. Нахождение первообразнойдля данной функциинаназывается интегрированием функции.

Свойства:

1. 

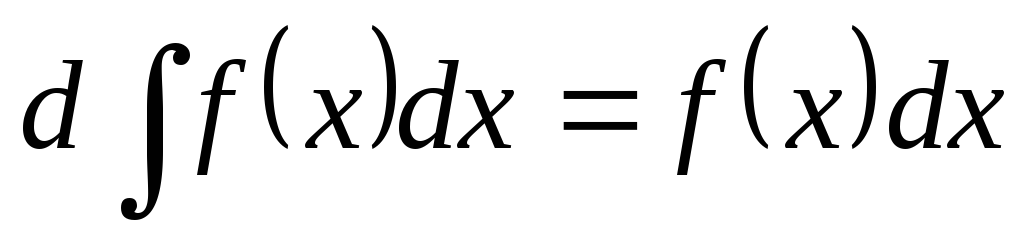
2. Так какимеет,т.е.то

3.

4.

5.

Таблица неопределенных интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

Замена переменной в неопределенном интеграле (2).

1. Внесение под знак дифференциала

2. Замена переменной

Сделаем подстановку . Причем она определена на, так, что существует обратная функция, определенная наи будем считать, что существует производнаяна. ТогдаЕслиимеет первообразную, то, таким образом после замены переменной в неопределенном интеграле и нахождение у первообразнойнеобходимо возвратиться к старой переменной.

Доказательства: Продифференцируем соотношениепоx, используя свойство (1) получим:

, что и требовалось доказать.

Пример:

, т.е. на практике чаще приходится делать обратную подстановку

Интегрирование по частям в неопределенном интеграле (3)

Пусть функции определены и дифференцируемы наи пусть подынтегральное выражениеможет быть представлено в виде:

, тогда

Доказательство: продифференцируем

и проинтегрируем по х.

или

. Отсюда

Существует несколько классов функций, которые могут быть проинтегрированы этим методом:

1. Интегралы, содержащие одну из функций lnx, arcsinx и т. д. Такие интегралы берутся методом интегрирования по частям, причем через U обозначается одна из этих функций(аdV, то что осталось).

2. Интегралы вида;;

интегрируются по частям при этом каждый раз в качестве U принимается многочлен.

3. Интегралы вида: ,,,

двукратное применение формулы интегрирование по частям в следствии получаем линейное уравнение относительно исходного интеграла а решая которое и находим искомый интеграл.

Прим.: №1

№2

4. Существуют и другие типы неопределенных интегралов, которые могут быть вычислены применением формулы интегрирования по частям.

Пример:

Разложение рациональной дроби на простейшие (4).

Отношение 2х мн-нов иназ.рац. дробью.

–рац. дробь.

m – порядок мн-на

n – порядок мн-на

Если , то рац. дробьназ.неправильной рац. др.

–непр. рац. дробь.

–пр. рац. дробь.

Если же m < n, то рац. дробь –пр. рац. дробь.

Любую правильную рациональную дробь можно разложить на сумму простейших дробей вида:

. Правильные рациональные

дроби вида I-IV называется простейшими рациональными дробями.

Теорема № 1: Если многочлен Q(x) имеет корень а кратности , т. е.Q(x)=(x-a), где Q₁(a) 0, то правильная рациональная дробь можно представить в видепричем последняя дробь правильная.Доказательство: Запишем тождество определимconst А таким образом чтобы многочлен делился нанацело т. е.А было корнем этого многочлена. (по теореме Безу) т. к.Q₁(a) 0 и P(a) 0 то А определим однозначно следовательно подстановка выраженияP(x)-AQ₁(x)=(x-a)+P₁(x) в тождество дает: Следствие № 1: К правильной рациональной дроби можно применить последовательно теорему № 1:

Следствие № 2: Если Q₁(x) имеет действительные корни, то к правильной рациональной дроби можно применить теорему № 1 и следствие № 1, т. е. если в правильной рациональной дробимногочлен имеет разложение, гдене имеет действительных корней.- действительные числа, торазложим на сумму дробейI,II и правильную рациональную дробь . Аналогично теорема имеет место и в том случае когда многочлен имеет комплексно сопряженные корни, т. е. раскладываются на квадратные трехчлены, где.

Теорема № 2: Если многочлен Q(x) имеет комплексно сопряженные корни a+bi кратности , т. е. имеют разложения видаQ(x)=(x²+px+q)Q₁(x), где (не имеет действительных корней), аQ₁(x) не делится на цело на x²+px+q, то правильная рациональная дробь можно представить в видепричем последняя дробь правильная.Доказательство: Как и при доказательстве теоремы № 1 стартуем с тождества коэффициентыM и N определены однозначно если потребовать чтобы многочлен P(x)-(Mx+N)Q₁(x) делился на x²+px+q нацело т. е. по теореме Безу P(x)-(Mx+N)Q₁(x)=( x²+px+q)P₁(x) и P₁(x) на x²+px+q нацело не делится. Подставляя это выражение в тождество получаем .Следствие № 3: К правильные рациональные дроби можно применить теорему № 2 в результате правильная рациональная дробьразложена на сумму дробей видаIII, IV и правильная рациональная дробь со знаменателем Q₁(x), , если многочленQ₁(x) делится на Q₂(x), то к правильной рациональной дроби можно применить теорему № 2 и ее следствие № 3 т. о. Если многочленQ(x) имеет разложение , то правильную рациональную дробьможно разложить используя теоремы № 1 и № 2 и их следствия на сумму простейших дробей видаI-IV.

(5).