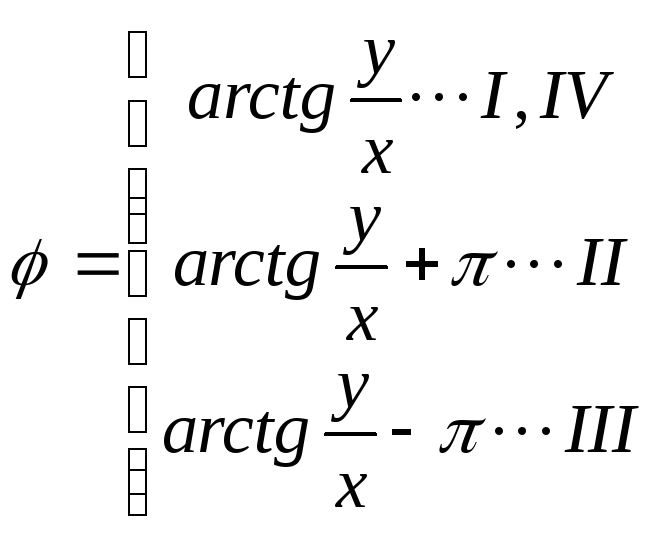шрора по в

1.М-ца размером (m*n) или m*n – м-цей над множеством М наз. Прямоугольная т-ца составленная из m*n элементов множества М и содержащее m стр. и n стл.

Сокр. обозначение м-ц:

М-цы равны между собой если равны все соответствующие элементы этих м-ц.

Диагон: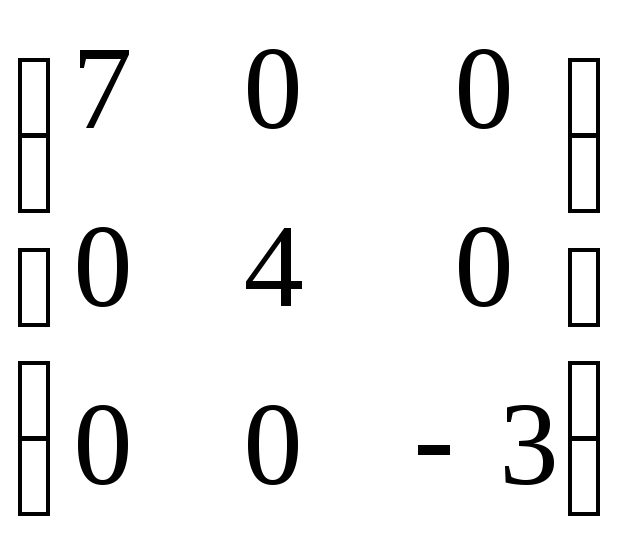Еденич: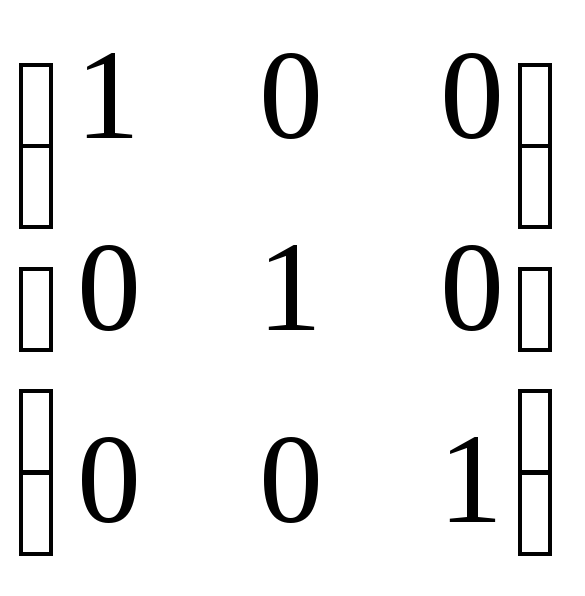сколяр: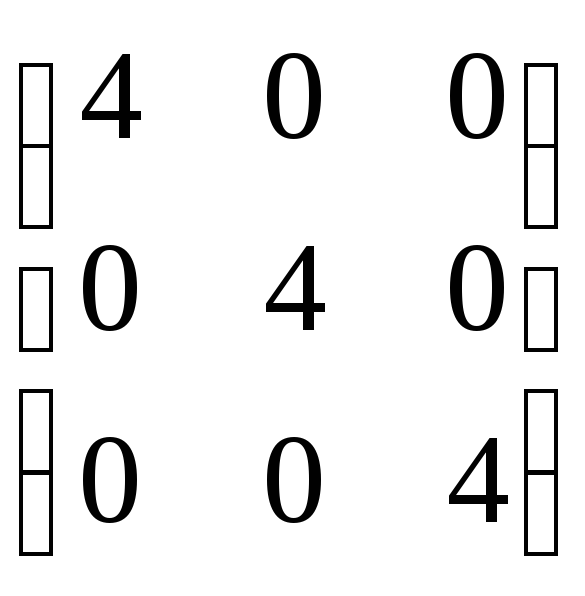треуг:

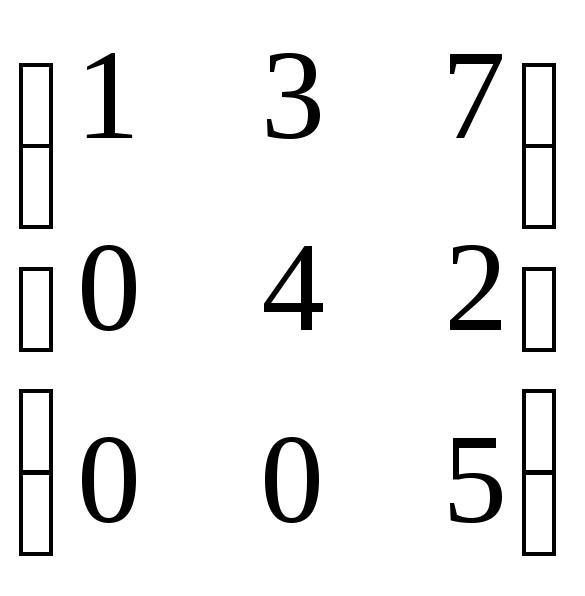
в-ор - стл: В-ор – стр: нулевая:

Транспонированноя: А=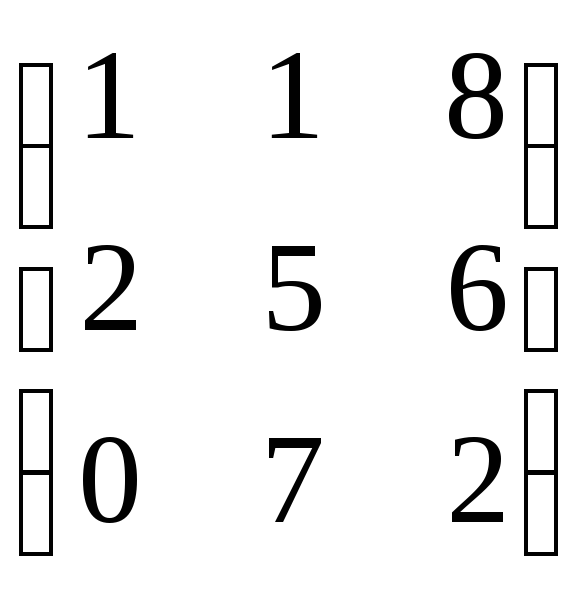 А^т =

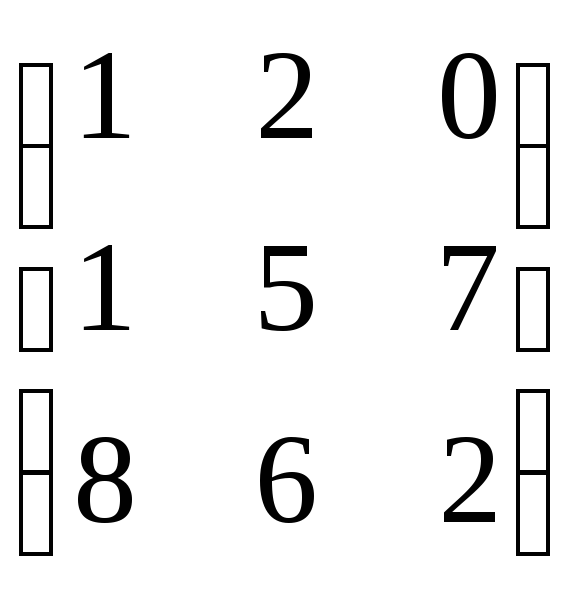
2. Сложение – операция слож. и вычитан. вводиться только для м-ц одинаковых размеров.

Суммой 2-х м-ц называется м-ца, где С_ij=a_ij+b_ij

Вычитание м-ц аналогично.

Произведением м-цы на число наз. м-ца, где b_ij=k*a_ij

Свойства:

1 Коммутативность: A+B=B+A

2 Ассоциативность: (А+В)+С=А+(В+С)

3 А+0=А А+(-А)=0

3. Операция умножения 2-х м-ц вводится только для случая когда число стл 1-й м-цы равно числу стр 2-й м-цы.

М-цы А и В назыв. перестановачными если А*В=В*А. В общем случаи это не верно.

4. Квадр. м-ца наз. не вырожденной если А0, в противном случаи вырожденная.

М-ца наз. обратной м-це А если выполняется условие м-ца Е того же порядка что и м-ца А. м-ца А^-1так же имеет тот же размер что и м-ца А. не забывать транспонировать матрицу

Любая невырожденная м-ца имеет обратную.

5 Опред квадр м-цы назыв число.

Свойства:

1

2 Если квадр м-це n-го порядка поменять между собой строки то определитель новой м-цы равен определителю исходной м-цы, взятому со знаком минус.

3 Опред имеющий 2-е одинаковые строки равен нулю.

4 Если все элементы i-ой строки имеют общий множитель m, то его можно вынести.

5 Если элементы 2-х различных стр м-цы пропорциональны, то опр = 0

6 Если каждый элемент какой либо строки представляет собой сумму 2-х слагаемых, то разложить на два!!!

7 Если к элементам i-ой стр прибавить соответст элементы j-ой стр этой м-цы, умноженные на одно и то же число m, то получаем м-цу, опред которых равны.

8 Определитель квадр. м-цы n-го порядка у которой все элементы некоторой стр равны нулю, то опред равен нулю.

9 Опред диагональной м-цы равен произведению диагональных элементов.

10

Опред основной м-цы должен быть не равен нулю.

Опред не квадратной м-цы находиться по разложению элементов.

6. Формулы КРАМЕРА:

(1) находим и подставляем вместо потом подставляем в формулу 1, так находим иксы.

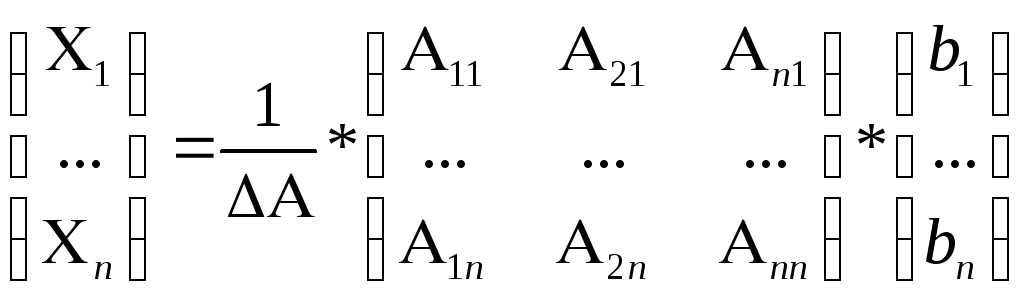
7. Матричный способ:

(6) Отыскание решения системы по формуле 6 наз м-чным методом решения

8. Наибольший из порядков миноров (m) м-цы А_m*n отличных от нуля называется рангом м-цы r(A)

Минор (определитель) порядок которого определяет ранг м-цы, наз Базисным их может быть несколько.

Ранг ступенчатой м-цы равен числу её не нулевых строк. (все нули – нул стр.)

Свойства ранга:

1 При транспонировке м-цы её ранг не меняется.

2 Если вычеркнуть из м-цы нулевой ряд то её ранг не меняется.

3 Ранг м-цы не меняется при элементарных приобразованиях м-цы:

а) Перестановка двух парал рядов м-цы.

б) Умножение всех элементов ряда м-цы на число не равное нулю

в) Прибавление ко всем элементам ряба м-цы соответствующих элементов парал ряда умноженных на одно и тоже число.

Решение по методу Гаусса:

1 этап: (прямой ход)Система приводится к ступенчатому виду.

2 этап: (обратный ход) Идёт последовательное определение неизвестных из ступенчатой м-цы. И потом проверка!!!

Вектора:

=(a_x a_y a_z )– координаты

Направляющие косинусы в-ра:

и аналогично

- длина

Нахожд точки деления в отношении ()

y,z – аналогично

- СкП

-ф-ла СкП

- разложение по базису

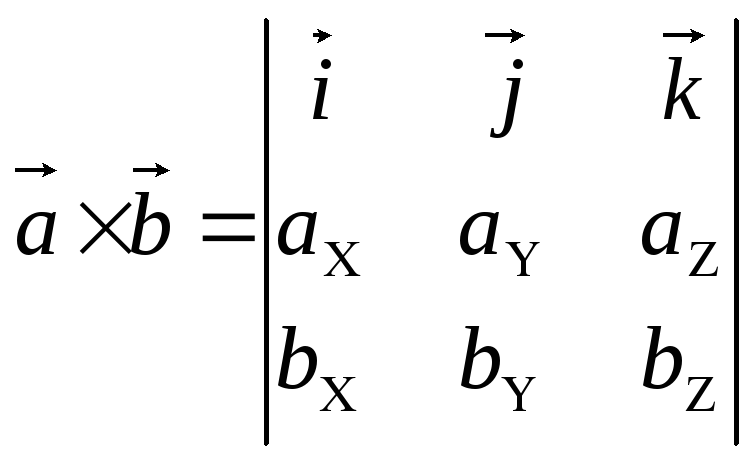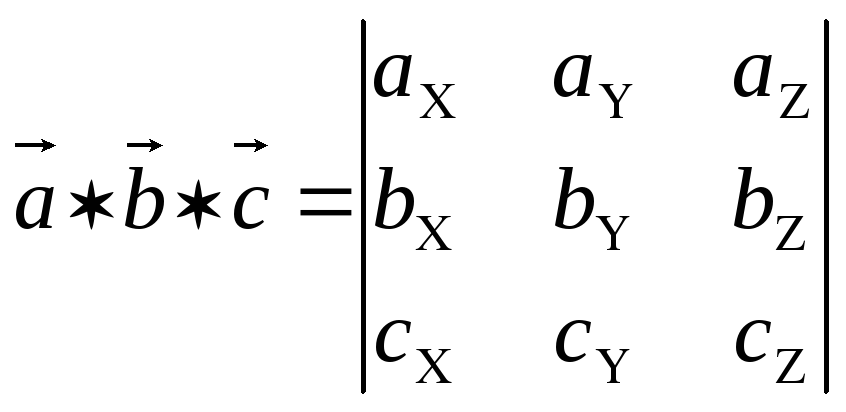- ВП - СмП

Линии на п-ти:

- окружность

- ур-ие параметрическое

- общее у-ние прямой

- у-ние прямой с угл коэфиц

//:к₁=к₂ :

- уравн прямой в отрезках на осях

у-ие прямой проход через заданную точку

- если известны 2 точки

-у-ие прямой прохлд через 2 точки

- ур прямой проходящей через данную точку данному в-ру

-нормальное уравнение прямой Р-растояние

- прямой //-на данному вектору (каноническое у-ие прямой)

- параметрическое у-ие прямой

- угол между двумя прямыми:

-растояние от точки до прямой

П-ти в пространстве:

- ур п-ти в пространстве

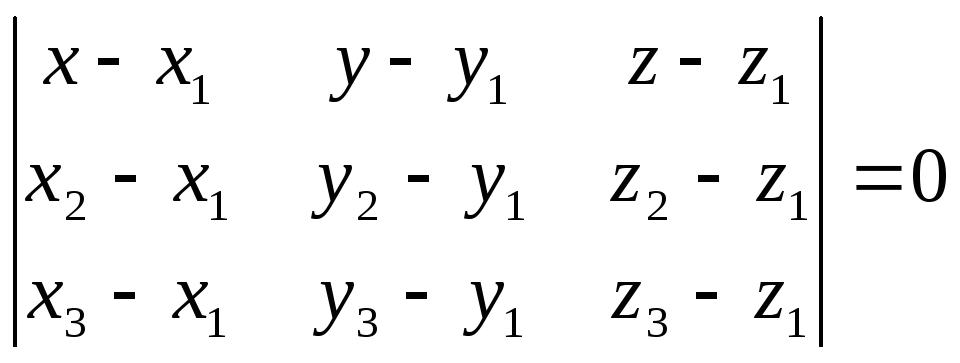- п-ть проход через 3 точки

- п-ть в отрезках на осях

-норм ур-ие п-ть;; Р-длина перпенд из нач координ на п-ть.

- нормирующий множитель

-касательная

-нормаль

Кривые 2-го порядка:

-кривая 2-го порядка

-канон ур-ние окружности

-канон ур-ние эллипса

-сопряжённая гипербола

- равнобочная гипербола

- парабола

Поверхности 2-го порядка:

-сфера

-парабол цилиндр

- круговой цилиндр

-элипсойд

-однополосный гиперболойд

-двухполосный гиперболойд

-эллиптический параболойд

-гиперболический параболойд

-конус 2-го порядка

Комплексные числа:

Алгебраически:

надо домнож на сопрежён

Тригонометрическая:

k=n-1

Показательная: