6.4 Определение изгибающих моментов

1 Изображают схему нагружения зубчатых колес и по формулам (см. рисунки 6.9 и 6.10) определяют силы, действующие в зацеплении. Для построения эпюр силы, действующие в зацеплении, переносятся на осевую линию вала. Схемы нагружения вала и эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях строятся раздельно.

2 Изображают схему сил, действующих на каждый вал в вертикальной и горизонтальной плоскостях.

3 Строят эпюры изгибающих моментов в вертикальной плоскости отдельно от всех действующих сил, а для получения общей эпюры наибольшего изгибающего момента все эпюры суммируют.

4 Выполняют то же, что и в п. 3, только уже в горизонтальной плоскости – .

5 Устанавливают опасное сечение вала и определяют общий изгибающий момент от действия сил в вертикальной и горизонтальной плоскостях:

6 С учетом крутящего момента определяют приведенный момент в опасных сечениях вала:

7 Определяют диаметры валов в опасных сечениях из условия

где– допускаемое напряжение изгиба, МПа, при расчете зубьев колеса или шестерни на выносливость (усталость).

Если опасное сечение вала ослаблено шпоночной канавкой, то диаметр вала нужно увеличить на 8 – 10 %.

8 Для подбора подшипников качения необходимо определить суммарные реакции в опорах подшипников

.

Ниже приводятся примеры построения эпюр изгибающих моментов для валов двухступенчатого цилиндрического редуктора с косозубой и прямозубой ступенями, а также для коническо-цилиндрического и червячно-цилиндрического редукторов.

6.4.1 Построение эпюр изгибающих моментов для валов двухступенчатого цилиндрического редуктора с косозубой и прямозубой ступенями (рисунок 6.11)

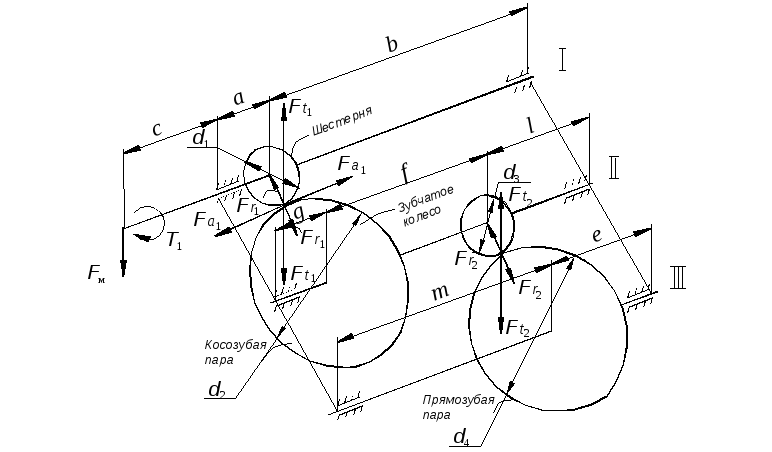
Косозубая пара: Прямозубая пара:

; ;;;

; ;.

Рисунок 6.11 – Схема нагружения зубчатых колес двухступенчатого цилиндрического редуктора с прямозубой и косозубой ступенями силами, действующими в зацеплении

Расчетная схема сил, действующих на вал I, и построение эпюр изгибающих моментов.

На валIдействуют (рисунок 6.12):

а) в вертикальной плоскости – силы F_ми;

б) в горизонтальной – силы и. Эти силы изгибают вал соответственно в вертикальной и горизонтальной плоскостях;

в) крутящий момент на участке от муфты до шестерни.

Рисунок 6.12 – Схема сил, действующих на вал I в вертикальной и горизонтальной плоскостях, и эпюра крутящих моментов

1

а) силы идействующие на валI в вертикальной плоскости

б) эпюра изгибающего момента от силы

в) эпюра изгибающего момента от силы

г) общая эпюра изгибающих моментов и. (Ординаты на эпюрах показаны ориентировочно, так как силыиданы в общем виде)

д) общая эпюра изгибающих моментов ипри

Построение эпюр изгибающих моментов валаI в вертикальной плоск ости(рисунок 6.13).

Рисунок 6.13 – Схема сил идействующих на валI в вертикальной плоскости (а), и эпюры изгибающих моментов от этих сил (б–д)

Так как силы и даны в общем виде, то построим эпюры изгибающих моментов в вертикальной плоскости отдельно от силы и от:

а) определяем опорные реакции от силы (рисунок 6.13,б):

Проверка:

Наибольший изгибающий момент будет в сечении вала на опоре А:

;

б) определяем опорные реакции от силы (рисунок 6.13,в):

Проверка:

Наибольший изгибающий момент будет в сечении вала, где приложена сила :

Для получения общей эпюры изгибающих моментов в вертикальной плоскости необходимо просуммировать две полученные эпюры (рисунок 6.13, г).

2 Построение эпюр изгибающих моментов вала I в горизонтальной плоскости(рисунок 6.14):

а) определяем опорные реакции от силы (рисунок 6.14,б):

Наибольший изгибающий момент будет в сечении вала, где посажена шестерня,

;

а) силы и, действующие на валI в горизонтальной плоскости

б) эпюра изгибающего момента от силы

в) эпюра изгибающего момента от силы

Рисунок 6.14 – Схема сил и, действующих на валI в горизонтальной плоскости (а), и эпюры изгибающих моментов от этих сил (б, в)

б) определяем реакции от силы (рисунок 6.14,в):

Наибольший изгибающий момент будет в сечении вала, где приложена сила ,

или

Имея конкретные значения сил и, а также расстоянияа,b иd₁, можно построить суммарную эпюру изгибающих моментов в горизонтальной плоскости. Наибольший изгибающий момент

Учитывая изгибающие моменты в вертикальной и горизонтальной плоскостях, найдем расчетный изгибающий момент в опасном сечении (в месте посадки шестерни):

Расчетная схема сил, действующих на вал II, и построение эпюр изгибающих моментов (рисунок 6.15).

На вал IIдействуют:

а) крутящий момент между зубчатым колесом 2 и шестерней 3;

б) изгибающий момент в вертикальной плоскости от окружных сил и;

в) изгибающий момент в горизонтальной плоскости от радиальных сил ии осевой силы.

1 Построение эпюр изгибающих моментов в вертикальной плоскости от сил и. Определение опорных реакций от сили:

.

.

Проверка:

Изгибающий момент в сечении вала в месте посадки зубчатого колеса 2

.

Изгибающий момент в сечении вала в месте посадки зубчатого колеса 3

2Построение эпюр изгибающих моментов в горизонтальной плоскостиот действия радиальных сил ии отдельно от действия осевой силы(рисунок 6.16):

Рисунок 6.15 – Схема сил, действующих на вал II, и эпюры изгибающих моментов от сил и, действующих в вертикальной плоскости

Рисунок 6.16 – Схема сил, действующих на вал II в горизонтальной плоскости, и эпюры изгибающих моментов от действия радиальных сил ии от осевой силы

а) определение опорных реакций от сил и:

Проверка:

Изгибающие моменты в сечениях 2 и 3 будут соответственно равны:

б) определение опорных реакций от силы :

Проверка:

При конкретных значениях ,,,d₂,g,fиlстроится суммарная эпюра изгибающих моментов в горизонтальной плоскости. Определяются суммарные реакции в горизонтальной плоскости в опорахСиD(в подшипниках):

Кроме того, на участке вала II между упорным подшипником и зубчатым колесом 2 действует продольная сжимающая сила, равная и– осевая реакция в упорном подшипнике (рисунок 6.17).

Анализируя полученные эпюры, находим, что опасными (наиболее нагруженными) для вала IIявляются сечения в местах посадки зубчатого колеса 2 и шестерни 3.

Расчетные изгибающие моменты в этих сечениях находим по формуле

С учетом крутящих моментов находим приведенные моменты в опасных сечениях:

Находим суммарные реакции в опорах подшипников вала II:

опора С(упорный подшипник) радиальная реакция;

опора D(опорный подшипник) радиальная реакция.

Расчетная схема сил, действующих на вал III, и построение эпюр изгибающих моментов(рисунок 6.18). На валIIIдействуют:

а) крутящий момент между зубчатым колесом 4 и подшипником ;

б) изгибающий момент в вертикальной плоскости от окружной силы ;

в) изгибающий момент в горизонтальной плоскости от радиальной силы .

1 Построение эпюр в вертикальной плоскостиот силы .Определение опорных реакций:

Проверка:

2 Построение эпюр в горизонтальной плоскости от силы .Определение опорных реакций:

Проверка:

Наибольший изгибающий момент в горизонтальной плоскости будет в сечении 4 – в месте посадки зубчатого колеса 4:

Анализируя полученные эпюры, находим, что опасным является сечение 4. Расчетный изгибающий момент в этом сечении

С учетом изгибающего и крутящего моментов определяем приведенный момент в опасном сечении 4:

Находим суммарные реакции в опорах подшипников ЕиF:

опора Е: опораF: