16.2 Пример расчета привода с цилиндрическим двухступенчатым соосным редуктором и цепной передачей

16.2.1 Исходные данные для проектирования

Рассчитать привод к цепному конвейеру по схеме, показанной на рисунке 16.7.

Исходные данные:окружное усилие на тяговых звездочкахокружная скорость этих звездочекшаг тяговых цепейчисло зубьев тяговых звездочек

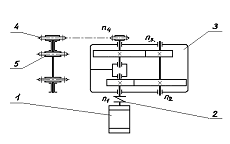
Привод включает цилиндрический двухступенчатый соосный редуктор (рисунок 16.8) и цепную передачу.

Рисунок 16.7 – Кинематическая схема привода цепного конвейера: 1 – электродвигатель; 2 – муфта упругая; 3 – редуктор зубчатый цилиндрический соосный; 4 – цепная передача; 5 – тяговые звездочки конвейера

Рисунок 16.8 – Кинематическая схема зубчатого цилиндрического двухступенчатого соосного редуктора

16.2.2 Расчет привода

Выбор электродвигателя.

Требуемая мощность электродвигателя определяется по формуле

где – общий КПД привода;

.

По данным, приведенным в таблице 4.2, принимаем:

– КПД зубчатой передачи с цилиндрическими колесами, работающей в масляной ванне (= 0,98);– КПД цепной передачи (= 0,92);– КПД, учитывающий потери в одной паре подшипников качения (= 0,99);– КПД, учитывающий потери в паре подшипников скольжения (вал барабана смонтирован на подшипниках скольжения (= 0,98)).

Тогда на основании полученных данных по приложению А.4 выбираем короткозамкнутый трехфазный асинхронный электродвигатель серии 4А90L4У3;

Примечание. Габаритные, установочные и присоединительные размеры и масса двигателей в зависимости от формы исполнения двигателей приведены в источнике [28, т. 3].

Определяем мощности на валах привода:

Кинематический расчет привода.

Определяем частоту вращения ведомого вала привода или ведущего вала ведомой звездочки:

Общее передаточное число

Производим разбивку передаточного числа по ступеням согласно рекомендациям таблицы 4.2. Так как редуктор является соосным, то принимаем предварительно тогда передаточное число редуктораа передаточное число цепной передачи

Определяем частоты вращения валов привода:

ведущего вала редуктора промежуточного вала редуктораведомого вала редуктора и одновременно вала ведущей звездочки вала ведомой звездочки

Определяем крутящие моменты на валах:

на ведущем валу редуктора

на промежуточном валу редуктора

на ведомом валу редуктора (он же и на валу ведущей звездочки)

на валу ведущей звездочки

Определяем ориентировочно диаметры всех валов привода:

или

или

или

или

16.2.3 Расчет редуктора

Выбор материалов для зубчатых колес. Желая получить сравнительно небольшие габариты и невысокую стоимость редуктора, выбираем для изготовления колес и шестерен сравнительно недорогую легированную сталь 40Х. По таблице 4.4 назначаем для колес термообработку: улучшение 230…260HB, = 850 МПа, = 550 МПа, для шестерни второй ступени – улучшение 260…280 НВ = 950 МПа, = 700 МПа; зубьям шестерни первой ступени – азотирование поверхности 50…59HRCпри твердости сердцевины 26…30HRC, = 1000 МПа, = 800 МПа. При этом обеспечивается приработка зубьев обеих ступеней [30, с. 164, 178].

Определение допускаемых контактных напряжений

Допускаемые контактные напряжения для второй ступени определяем по материалу колеса, как более слабому, по формуле

,

где – предел контактной выносливости, определяется по таблице 4.5;для шестерни первой ступени(азотирование);

K_HL – коэффициент долговечности при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора; принимаютK_HL = 1.

Определяем рабочее число циклов напряжений для колеса второй ступени по формуле

где – суммарный срок службы, называемый ресурсом передачи, или число часов работы передачи за расчетный срок службы;

n– частота вращения того из колес, по материалу которого определяют допускаемые напряжения;

с – число зацеплений зуба за один оборот колеса (сравно числу колес, находящихся в зацеплении с рассчитываемым).

Базовое число циклов определяем по графику (см. рисунок 4.6,б) в зависимости от твердости зубьев колеса. При твердости зубьев колеса НВ 240. Так как расчетное число цикловбольше базового, то коэффициент долговечности принимаем[32, с. 190]. Так как все другие колеса вращаются быстрее, то и для них >, а следовательно, для всех колес редуктора

Коэффициент безопасности (см. таблицу 4.5) для первой ступени, для второй ступени.

Допускаемые контактные напряжения для второй ступени определяем по материалу колеса как более слабому

Для колеса первой ступени также а для шестерни

Допускаемое контактное напряжение для первой ступени определяем по формуле

Так как поэтому принимаем

Определение допускаемых напряжений изгиба

Определяем допускаемые напряжения изгиба по формуле

где – предел выносливости зубьев по напряжениям изгиба; определяется по таблице 4.5: для колес обеих ступенейдля шестерни первой ступени при азотировании поверхностидля шестерни второй ступени

– коэффициент безопасности; выбираем по таблице 4.5,

– коэффициент, учитывающий влияние двустороннего приложения нагрузки (например, реверсивные передачи, сателлиты планетарных передач и т.д.). В данном случает.к. действует односторонняя нагрузка.

Коэффициент долговечности принимаем равным 1. Его расчет аналогичен расчету, но базовое число циклов рекомендуется приниматьдля всех сталей [30, с. 174].

Тогда для обоих колес

для шестерни второй ступени

для шестерни первой ступени

Определение опускаемых напряжений при кратковременной перегрузке

Предельные контактные напряжения для колес обеих ступеней

для шестерни второй ступени

для шестерни первой ступени .

Предельные напряжения изгиба для обоих колес определяем по таблице 4.5:

для шестерни второй ступени

для шестерни первой ступени при азотировании

Расчет второй тихоходной прямозубой пары (u= 3).

Расчет начинается со второй тихоходной прямозубой пары как более нагруженной и, в основном, определяющей габариты редуктора.

Определяем межосевое расстояние и другие параметры:

где – приведенный модуль упругости;

– коэффициент концентрации нагрузки [30, с. 127–130]; определяется по графику (см. рисунок 4.9) в зависимости от– коэффициента ширины шестерни;

– коэффициент ширины колеса относительно межосевого расстояния [30, с. 135]; принимается по рекомендациям таблицы 4.6,

Определяем для симметричного расположения колес относительно опор (см. рисунки 4.8, 4.9).

.

Округляем расчетное значение для нестандартных редукторов по ряду:40: …80, 85, 90, 95, 100, 105, 110, 120, 125, 130, далее через 10 до 260 и через 20 до 420…

Тогда принимаем

Находим ширину колеса:

По таблице 4.7 выбираем

Тогда модуль: .

По таблице 4.8, согласуясь со стандартом, назначаем модуль

Суммарное число зубьев:

Число зубьев шестерни:

Принимаем [30, с. 143].

Число зубьев колеса:

Фактическое передаточное число определим из соотношения

Делительные диаметры шестерни и колеса определяются по формулам:

Выполняем проверочный расчет на усталость по контактным напряжениям:

где – коэффициент расчетной нагрузки; определяется по формуле

Т₁ =Т₂;

– коэффициент динамической нагрузки; определяется по таблице 4.10.

По таблице 4.11 назначаем 8-ю степень точности. в зависимости от степени точности и окружной скорости колеса

.

Тогда [30, с. 116].

Тогда .

Примечание. Если значенияирасходятся более чем на4 %, то их можно сблизить путем изменения ширины колес по условию, которое следует из формулы.

Выполняем проверочный расчет по напряжениям изгиба:

где – коэффициент формы зуба. По графику (см. рисунок 4.10) принаходим: для шестернидля колеса

– коэффициент расчетной нагрузки;.

Расчет выполняем по тому из колес пары, у которого меньше

В нашем случае: ;

Расчет выполняем по колесу.

По графику (см. рисунок 4.9) По таблицепри окружной скорости колеса:При этом

Далее

Тогда

Выполняем проверочный расчет на заданную перегрузку по формулам

Условие прочности соблюдается.

Расчет первой быстроходной косозубой пары (u= 3).

Так как редуктор соосный, то межосевые расстояния для двух ступеней будут одинаковы. Таким образом, принимаем

Определяем параметры шестерни и колеса. Для определения ширины колес используем формулу

По таблице 4.6 принимаем , получим:

Ширину колеса принимаем

По таблице 4.7 выбираем Тогда модуль определяем по формуле.

По таблице 4.8, согласуясь со стандартом, назначаем модуль m = 1 мм.

Определяем угол наклона зубьев из формулы

,

где – коэффициент осевого перекрытия. Рекомендуют принимать. Принимаем.

Определяем .ТогдаВо избежание больших осевых сил в зацеплении рекомендуют приниматьдля шевронных колес допускают до 30 и даже до 40 [30, с. 146].

Определяем суммарное число зубьев

Число зубьев шестерни

Принимаем Число зубьев колеса определяем по формулеФактическое передаточное число определяется из соотношенияУточняем значениепо межосевому расстоянию по формуле

Тогда

Делительные диаметры шестерни и колеса получаем по формуле [30, с. 144]:

Выполняем проверочный расчет на усталость по контактным напряжениямпо формуле

где Т₁=Т_II;

– коэффициент повышения прочности косозубых передач по контактным напряжениям; определим по формуле

где – коэффициент, учитывающий ошибки при нарезании зубьев, выбирается по таблице 4.12 в зависимости от окружной скорости и степени точности;– коэффициент торцового перекрытия; определяется по формуле

;

Тогда .

Определяем окружную скорость колеса:

тогда

– коэффициент расчетной нагрузки;

– коэффициент динамической нагрузки; определяется по таблице 4.10.

По таблице 4.11 назначаем 8-ю степень точности. в зависимости от окружной скорости колеса и назначения передачи;

– коэффициент концентрации нагрузки [30, с. 127, 130]; определяется по графику (см. рисунок 4.9) в зависимости от– коэффициента ширины шестерни,что не превышает опускаемых максимальных значений (см. таблицу 4.6);

Тогда откуда

Такое расхождение типично для первой быстроходной ступени двухступенчатых редукторов [73, с. 257].

Выполняем проверочный расчет по напряжениям изгиба:

,

По графику рисунок 4.10 при находим: для шестернидля колеса– коэффициент расчетной нагрузки; определяется по формуле.

Расчет выполняем по тому из колес пары, у которого меньше

В нашем случае

Расчет выполняем по колесу.

По графику (см. рисунок 4.9) По таблице 4.10при окружной скорости колеса

При этом

Далее

– коэффициент повышения прочности косозубых передач по напряжениям изгиба; определяется по формуле

где – коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии к основанию зуба и неравномерного распределения нагрузки, определяется по формуле

,

в нашем случае

;

– коэффициент неравномерности нагрузки одновременно зацепляющихся пар зубьев, определяется по таблице 4.12 в зависимости от степени точности и окружной скорости колеса

Тогда

Выполняем проверочный расчет на заданную перегрузку

Условия прочности соблюдаются.