Группа 2 – больные.

Проведем оценку статистических совокупностей на принадлежность к нормальному закону распределения.

Переменная Дб1

Критерий хи-квадрат проверки распределения на нормальность

Объем выборки N=43. Число степеней свободы k=6. Chi-square=15,700, уровень значимости p=0,015

Распределение отличается от нормального на уровне значимости p=0,015

Переменная Кр1

Критерий хи-квадрат проверки распределения на нормальность

Объем выборки N=43. Число степеней свободы k=5. Chi-square=9,660, уровень значимости p=0,085

Распределение не отличается от нормального на уровне значимости, p=0,085

Переменная Тс1

Критерий хи-квадрат проверки распределения на нормальность

Объем выборки N=43. Число степеней свободы k=6. Chi-square=17,700, уровень значимости p=0,007

Распределение отличается от нормального на уровне значимости p=0,007

Проведем расчет описательной статистики:

Рассмотрим доверительный интервал:

График:

Построим гистограммы уровня гормонов кортизола (Кр) и тестостерона (Тс):

На основе выводов о нормальности распределения определим существование статистических различий длительности заболевания от показателей гормонов кортизола и тестостерона в группе больных. Воспользуемся критерием хи-квадрат:

Вывод:

Сравнение формы распределения двух выборок. Критерий хи-квадрат.

Переменные: Кр1, Тс1.

Хи-квадрат=37,27, число степеней свободы k=5.

Распределения отличаются на уровне значимости p<0,001.

Сравним переменные кортизола и тестостерона в группе больных людей, используя W-критерий Вилкоксона:

Сравнение центральных тенденций двух независимых выборок. W-критерий Вилкоксона. Двусторонняя критическая область.

Переменные: Кр1, Тс1.

W=946,0.

Центральные тенденции отличаются на уровне значимости p<0,001.

Воспользуемся коэффициентом Спирмена с целью статистического изучения связи между выборками: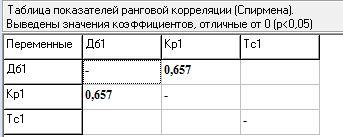

Определим взаимосвязь между выборками Кр и Тс, используя коэффициент корреляции Кендала:

Проверка значимости корреляционной связи для двух выборок. Коэффициент корреляции Кендалла.

Переменные: Дб1, Тс1.

Объем выборки: N=43.

Tau=0,045.

Корреляционная связь отсутствует, Tau=0, p>0,05.

Проверка значимости корреляционной связи для двух выборок. Коэффициент корреляции Кендалла.

Переменные: Дб1, Кр1.

Объем выборки: N=43.

Tau=0,503.

Существует корреляционная связь, Tau>0 (Tau=0,503) , на уровне значимости p<0,01.

Вывод: длительность болезни зависит от уровня кортизола, так как существует корреляционная связь, на уровне значимости p<0,01.Корелляционная связь длительности заболевания и уровнем тестостерона не обнаружена.

Выводы:

Знание медицинской статистики, будучи примененным в целях систематического критического анализа медицинских исследований, начинает давать нам новое, более научное понимание того, какие методы лечения полезны и экономически оправданы, а от каких можно отказаться безо всякого ущерба для наших пациентов. Медицинскую практику, основанную на таком новом знании, сегодня называют медициной, основанной на доказательствах. Она обещает повысить одновременно качество и экономическую эффективность медицинской помощи в экономически развитых странах.