3. Комплексный чертеж плоскости
Принадлежность прямой и точки плоскости. Взаимная параллельность прямой и плоскости, двух плоскостей
|
10. Достроить проекции произвольного плоского неправильного пятиугольника общего положения. В плоскости пятиугольника построить горизонталь h, фронталь f и профильную прямую p.
|
11. Через точку М провести плоскость∑', параллельно заданной плоскости ∑(ABCD), и равной половине площади заданной плоскости.
| ||
|
12. Достроить фронтальную проекцию отрезка [АВ], параллельного плоскости ∑(KLM).
| |||
|
13. Через прямую l провести: |
|
| |
|
а) горизонтально проецирующую плоскость ∑ под углом α=45° к П2
|
б)
фронтально проецирующую плоскость
|
в) профильно проецирующую плоскость Г под углом α=30° к П1
| |
|
14. Через точку О провести плоскость, заданную окружностью диаметром 40 мм с центром в точке О: а)
горизонтальную плоскость уровня ∑;
б) фронтальную плоскость уровня
| |||
.
;
в) профильную плоскость уровня
Г.
4. Комплексные чертежи гранных и кривых поверхностей.
ПРИНАДЛЕЖНОСТЬ ЛИНИИ И ТОЧКИ ПОВЕРХНОСТИ
Многогранники
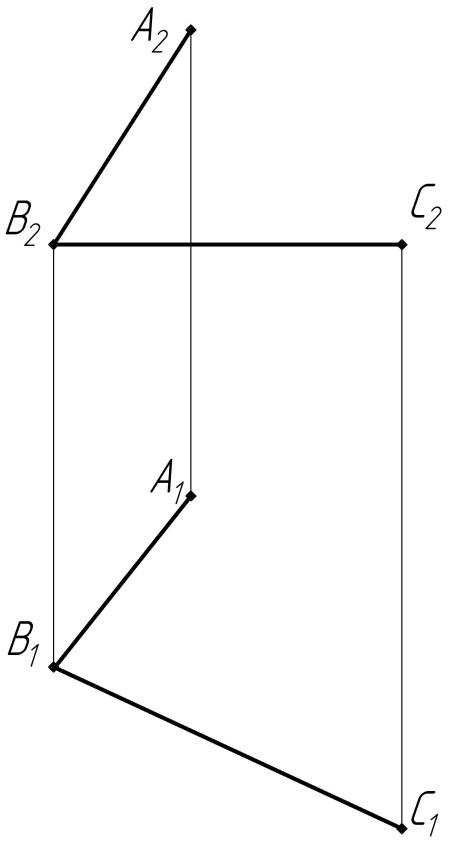
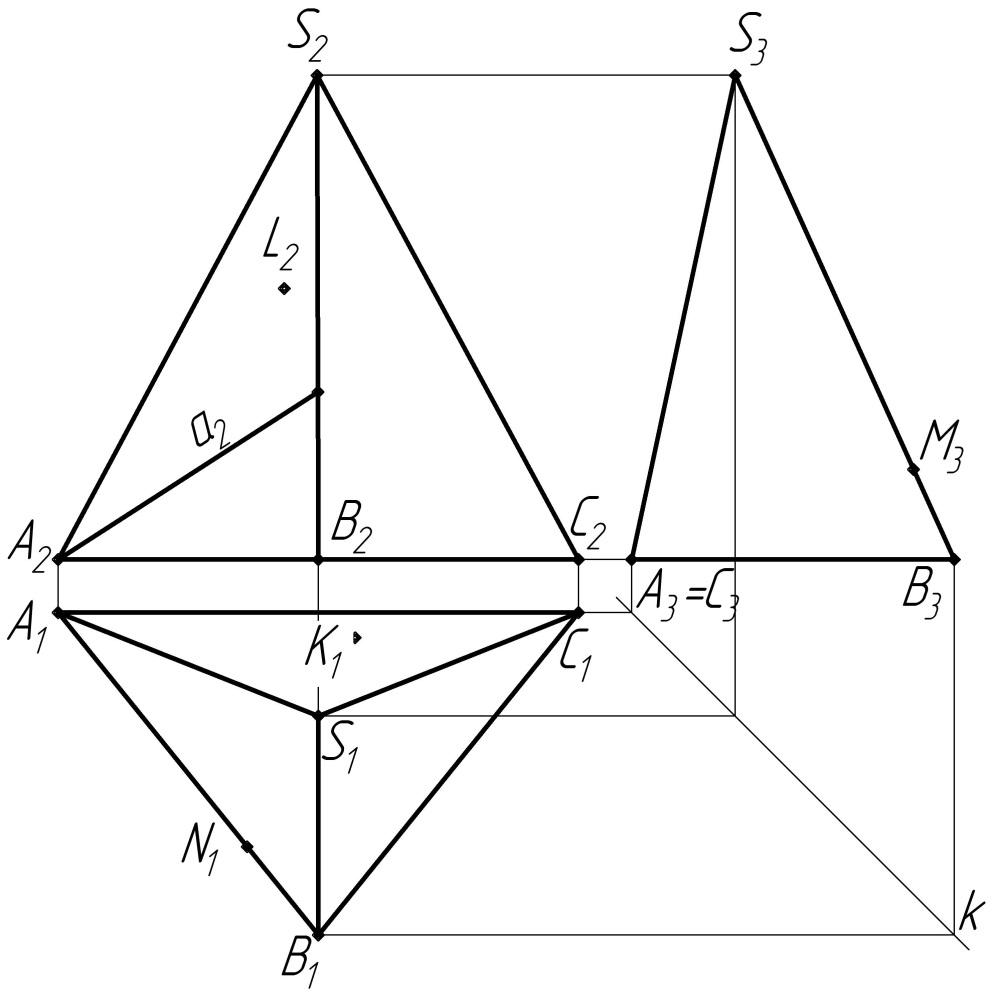
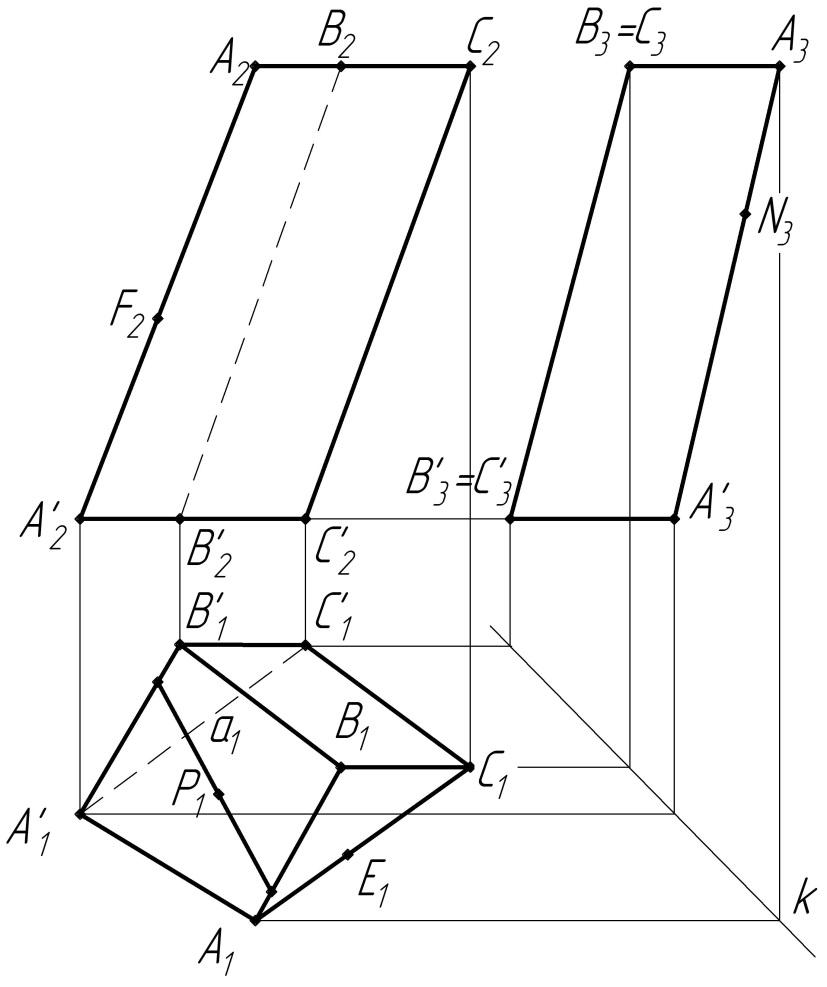
15. Построить недостающие проекции точек и линий, принадлежащих данным поверхностям. Заданные проекции точек и линии видимы.
|
1) Пирамиды
|
2) Призмы |
|
|
|
4.2. Кривые поверхности
16. Построить недостающие проекции точек и линий, принадлежащих данным поверхностям. Заданные проекции точек и линий видимые.
|
1) Конуса
|
2) Цилиндра |
|
|
|
|
3) Сферы
|
4) Тора |
|
|
|
5. ПОЗИЦИОННЫЕ ЗАДАЧИ. ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ПРЯМОЙ И ПОВЕРХНОСТИ;
ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ
5.1. Определение общих элементов простейших геометрических фигур из условия принадлежности
(Вспомогательные позиционные задачи)
При пересечении геометрических фигур с проецирующей плоскостью одна из проекций их общего элемента совпадает с проекцией проецирующей плоскости (которая вырождается в прямую линию). Поэтому решение этого типа задач сводится к построению второй проекции искомой геометрической фигуры.
|
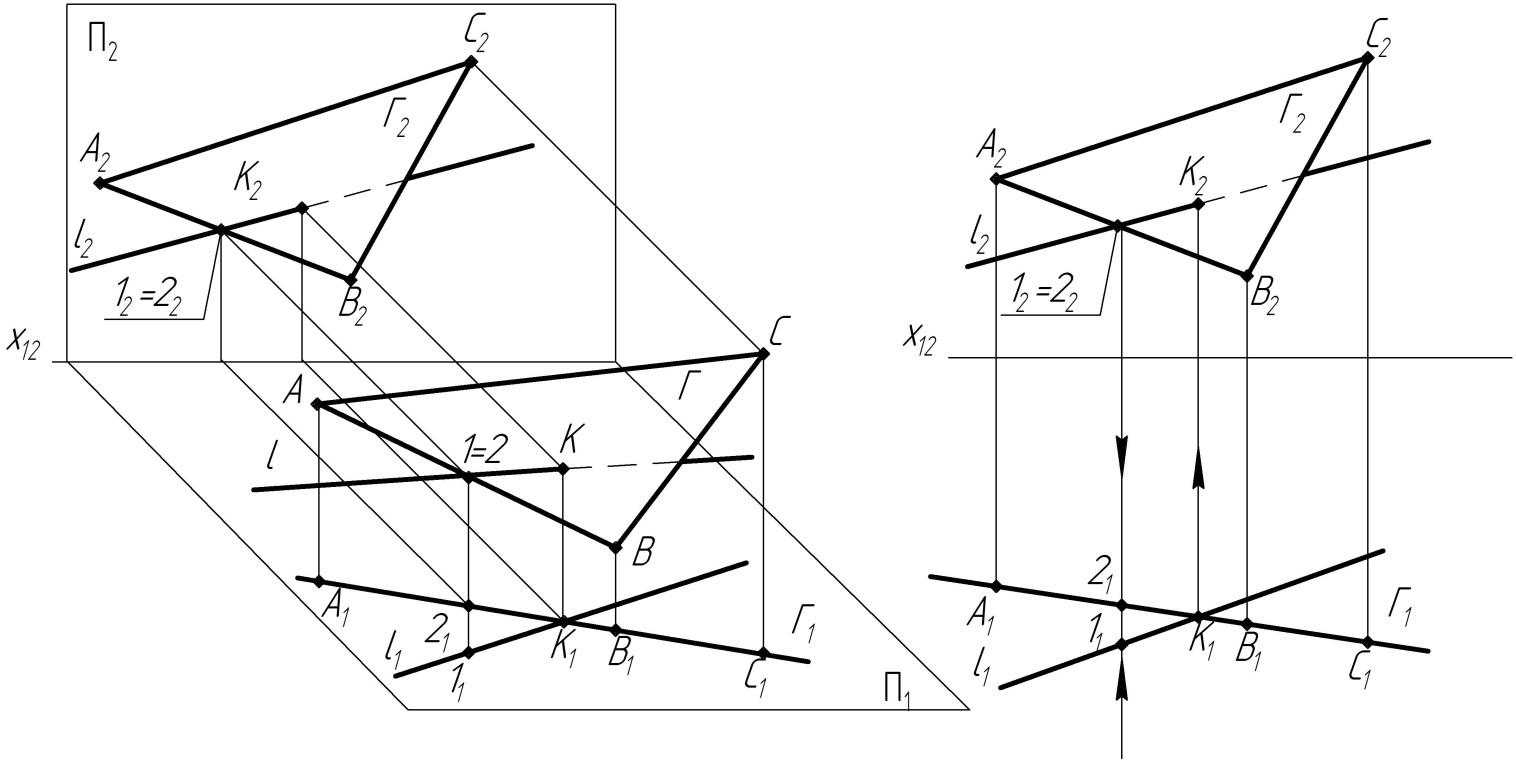
Задача. Построить точку К пересечения прямой общего положения l с горизонтально проецирующей плоскостью Г (рис. 3) |
| |
|
|
Решение
на комплексном чертеже представлено
на рис.4. Плоскость Г
пересекает линию l
в точке К,
горизонтальная проекция которой
определяется в пересечении горизонтальных
проекций проецирующей плоскости ∑
и прямой l.
Фронтальную проекцию точки К
определим по линиям связи по
принадлежности прямой l:
К2
| |
|
Рис.3 Рис.4 |
| |
|
17. Построить прямую k пересечения фронтально проецирующей
плоскости ∑
и плоскости Г(a
общего положения.
|
18. Построить прямую k пересечения двух фронтально проецирующих плоскостей.
| |
|
19. Построить линию k пересечения фронтально проецирующей плоскости ∑ и
плоскости Т(m
| ||
l2.
Видимость на П2
определим с помощью фронтально
конкурирующих точек 1
и 2.
Видим точку 1.
Принадлежащую прямой l.
Прямая l
видима до точки пересечения К,
в которой видимость меняется на
обратную.
b)
n).