
2_kurs / информатика / informatika_metodichka,2016
.pdfЗадачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых должен быть выяснен с помощью теоретического анализа) и оценки факторов, оказывающих наибольшее влияние на результативный признак.
Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчётных значений зависимой переменной (функции регрессии). Задача регрессионного анализа состоит в построении модели, позволяющей по значениям независимых показателей получать оценки значений зависимой переменной. Регрессионный анализ является основным средством исследования зависимостей между социально-экономическими переменными.
Более подробные теоретические сведения Вы можете получить, используя для подготовки указанную выше учебную литературу.
ЗАДАНИЯ ДЛЯ ДОСТИЖЕНИЯ КОНКРЕТНЫХ ЦЕЛЕЙ ОБУЧЕНИЯ ПО ТЕМЕ 16
ПРАКТИЧЕСКОЕ ЗАДАНИЕ № 1. С целью оценки влияния показателей обмена углеводов на состояние симпато-адреналовой системы у больных гипертонической болезнью, ассоциированной с иммунорезистентностью были проведены исследования показателей крови у 24 больных этой болезнью в возрасте 43
– 67 лет. Результаты исследования приведены в таблице.
Гликемия |
Уровень |
|
|
Уровень |
Уровень |
Уровень |
Уровень |
|
через 2 часа |
Уровень |
Уровень |
||||||
инсулина в |
альдостерона |
суточной |
липопротеидо |
липопротеидо |
||||
после |
общего |
триглицер |
||||||
плазме |
в плазме |
экскреции |
в высокой |
в низкой |
||||
нагрузки |
крови |
холестерина |
идов |
крови |
НА с мочой |
плотности |
плотности |
|
глюкозой |
(мМЕ/мл) |
(ммоль/л) |
(ммоль/л) |
(пкмоль/л) |
(нмоль) |
(ммоль/л) |
(ммоль/л) |
|
(ммоль/л) |
|
|
||||||
6,8 |
14,6 |
5,56 |
5,45 |
215 |
768 |
0,78 |
2,30 |
|
7,1 |
19,6 |
5,98 |
3,98 |
297 |
794 |
0,98 |
3,19 |
|
7,1 |
21,1 |
6,03 |
4,17 |
212 |
654 |
1,07 |
3,06 |
|
6,9 |
13,9 |
4,48 |
3,18 |
271 |
713 |
1,07 |
1,96 |
|
7,1 |
19,1 |
5,48 |
3,87 |
269 |
743 |
0,76 |
2,96 |
|
6,9 |
16,9 |
5,49 |
4,15 |
216 |
817 |
1,06 |
2,54 |
|
6,9 |
21,3 |
6,98 |
4,97 |
198 |
697 |
0,89 |
3,83 |
|
6,2 |
17,7 |
5,13 |
3,89 |
198 |
634 |
1,07 |
2,29 |
|
6,9 |
23,7 |
5,76 |
6,17 |
265 |
743 |
0,87 |
2,09 |
|
6,8 |
19,2 |
6,17 |
2,87 |
198 |
612 |
0,78 |
4,09 |
|
6,9 |
21,3 |
5,41 |
5,32 |
201 |
717 |
0,73 |
2,26 |
|
6,6 |
19,3 |
4,97 |
3,12 |
217 |
698 |
1,02 |
2,53 |
|
6,4 |
21,8 |
5,78 |
2,98 |
198 |
611 |
1,15 |
3,28 |
|
7,4 |
24,4 |
5,98 |
4,96 |
287 |
713 |
0,89 |
2,84 |
|
6,9 |
17,5 |
6,55 |
3,77 |
301 |
798 |
0,76 |
4,08 |
|
6,7 |
16,2 |
4,85 |
4,96 |
197 |
656 |
0,98 |
1,62 |
|
6,9 |
19,3 |
6,32 |
4,57 |
167 |
497 |
0,95 |
3,29 |
|
6,5 |
17,9 |
5,14 |
3,1 |
123 |
677 |
1,03 |
2,70 |
|
6,4 |
21,8 |
5,11 |
4,17 |
176 |
768 |
0,87 |
2,34 |
|
6,4 |
14,9 |
6,07 |
4,55 |
198 |
690 |
0,94 |
3,06 |
|
6,5 |
20,3 |
5,49 |
2,87 |
178 |
634 |
0,77 |
3,42 |
|
6,4 |
21,1 |
5,78 |
4,89 |
167 |
615 |
1,13 |
2,43 |
|
6,2 |
18,8 |
5,98 |
4,78 |
175 |
644 |
1,01 |
2,80 |
|
6,7 |
21,4 |
5,77 |
5,58 |
217 |
649 |
0,78 |
2,45 |
Выявить наличие корреляционной связи между анализируемыми признаками.
181

Используемые компьютерные программы:
1.Операционные системы: Linux
2.Прикладные программы общего назначения: O. Office Write, O. Office Calc.
3.Прикладные программы «StatMed», «MedStat».
Алгоритм выполнения практического задания 1:
Шаг -1. Представленные данные являются количественными – в программе MedStat
выберем пункт: Данные|Новые данные|Вариационный ряд и введем результаты.
Шаг -2. Проведем проверку распределения значений признаков на нормальность.
Шаг -3. Т. к. для всех анализируемых признаков распределение значений не отличается от нормального, p>0,05, то для проведения корреляционного анализа выберем параметрические критерии, соответствующий пункт – Линейная корреляция
(коэффициент Пирсона).
182

Шаг -4. Полученные результаты представим в виде отчета к практическому заданию.
Отчет.
Задание 1.
1)При проведении проверки распределения значений анализируемых признаков использовался критерий W Шапиро-Уилка.
Установлено, что для всех признаков распределение значений не отличается от нормального, p>0,05.
2)Т.к. распределение значений не отличается от нормального, то для проведения анализа используем параметрические критерии, для каждой пары признаков рассчитаем коэффициент линейной корреляции Пирсона.
Результат корреляционного анализа представим в таблице.
Таблица коэффициентов парной корреляции (Пирсона).
Переменные |
глюк |
инсулин |
ОХС |
ТГ |
альдосте |
НА |
ЛПВП |
ЛПНП |
|
2час |
рон |
||||||||
|
|
|
|
|
|
|
|||
глюк 2час |
- |
- |
- |
- |
0,669 |
- |
- |
- |
|
инсулин |
- |
- |
- |
- |
- |
- |
- |
- |
|
ОХС |
- |
- |
- |
- |
- |
- |
- |
0,774 |
|
ТГ |
- |
- |
- |
- |
- |
- |
- |
- |
|
альдостер |
0,669 |
- |
- |
- |
- |
0,583 |
- |
- |
|
НА |
- |
- |
- |
- |
0,583 |
- |
- |
- |
|
ЛПВП |
- |
- |
- |
- |
- |
- |
- |
- |
|
ЛПНП |
- |
- |
0,774 |
- |
- |
- |
- |
- |
*Выведены значения коэффициентов статистически значимо отличные от 0 (p<0,05)
3) На рисунке 1 представлено поле корреляции пары признаков для которых выявлена сильная корреляционная связь.
183

Рисунок 1. Поле корреляции показателей (r=0,774, отличен от нуля, p<0,001)
5) ВЫВОД.
При проведении корреляционного анализа значения показателей обмена углеводов и состояние симпато-адреналовой системы у больных гипертонической болезнью, ассоциированной с иммунорезистентностью выявлена положительная линейная корреляционная связь средней силы между показателем гликемии через 2 часа после нагрузки глюкозой и уровнем альдостерона в плазме крови (r=0,669, p<0,05), уровнем суточной экскреции НА с мочой и уровнем альдостерона в плазме крови
(r=0,583, p<0,05).
Выявлена также сильная положительная линейная корреляционная связь между уровнем общего холестерина и уровнем липопротеидов низкой плотности (r=0,774, p<0,05).
ПРАКТИЧЕСКОЕ ЗАДАНИЕ № 2. Построить и сравнить регрессионные зависимости частоты пульса от возраста в двух группах больных: 1 группа (возраст до 30 включительно) и 2 группа (возраст более 30). Выписать необходимые статистические показатели и коэффициенты корреляции. Сделать необходимые выводы. В табличном редакторе построить графики обнаруженных зависимостей. Данные представлены в файле ррр 1.mtv (ррр 1.ods).
Используемые компьютерные программы:
1.Операционные системы: Linux
2.Прикладные программы общего назначения: Open Office Write, Open Office
Calc.
3. Прикладные программы «StatMed», «MedStat».
Алгоритм выполнения практического задания № 1:
Шаг – 1. Включите компьютер. Дождитесь загрузки установленной операционной системы. Зайдите в меню “Start”.
184

Шаг – 2. В разделе учебные программы для студентов найдите и запустите программу
«StatMed».
Шаг – 3. Откройте директорию «Данные», выберите «Загрузить данные».
Шаг – 4. В открывшемся окне выберите файл ррр 1.mtv. Нажмите «Открыть».
185

Шаг – 5. Наведите курсор манипулятора «Мышь» на 1-й столбик «возраст», правой кнопкой «мыши» откройте меню и выберите позицию «Сортировать по возрастанию». Провести сортировку переменной “возраст” по возрастанию.
Шаг – 6. Сформируйте группу “до 30 лет”. Для этого поставьте курсор на строке данных с возрастом больше 30 лет и удалите все данные расположенные ниже.
186
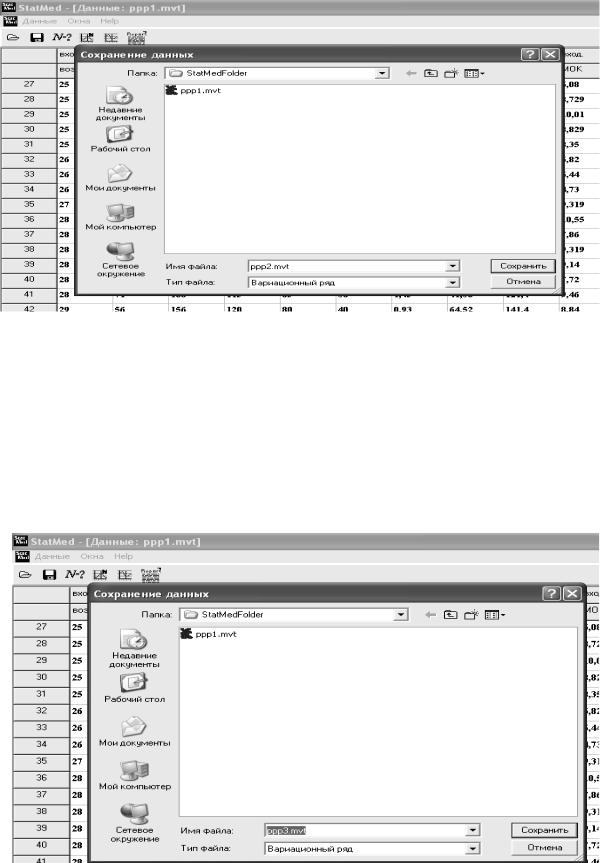
Шаг – 7. Сохранить полученные данные в файле под другим именем ррp2 (в папке
Documents / Student).
Шаг – 8. В программу «StatMed» повторно загрузить файл ррр 1.mtv. Наведите курсор «мыши» на 1-й столбик «возраст», правой кнопкой «мыши» откройте меню и выберите позицию «Сортировать по убыванию». Провести сортировку переменной “возраст” по убыванию. Наведите курсор «мыши» на 1-й столбик «возраст», правой кнопкой «мыши» откройте меню и выберите позицию «Сортировать по возрастанию». Провести сортировку переменной “возраст” по возрастанию и сформируйте группу лиц “старше 30 лет” по вышеприведенной методике (Шаг-5 …..Шаг - 7).
Шаг – 9. Сохранить полученные данные в файле под другим именем ррp 3 (в папке
Documents / Student).
187

Шаг –10. Откройте файлы ррр 2 и ррр 3. Скопируйте данные файла ррр 3 в файл ррр 2, установив показатели 2 группы справа от данных 1 группы. Для этого выделите данные в файле ррр 3, нажав клавиши «Shift» + «←», «→», «↓». Скопируйте выделенные данные в «буфер обмена», нажав сочетание клавиш «Ctrl» + «Insert». В случае необходимости переименуйте столбцы во 2-й группе.
Шаг – 11. Проведите статистические тесты на принадлежность совокупностей к нормальному закону распределения, рассчитайте в соответствии с этим описательные статистики для рядов частоты пульса (ЧП) в двух группах. Результаты сохраните и запишите в тетрадь.
188

Шаг – 12. Постройте график распределения совокупностей. Сохраните результаты в текстовый файл, запишите в тетрадь.
Шаг – 13. На основе выводов о нормальности распределения определите существование статистических различий показателя частоты пульса в двух возрастных группах.
189

Шаг – 14. Рассчитать коэффициенты корреляции в каждой группе и сравнить их.
Шаг – 15. Постройте графики простой линейной регрессии (зависимость частоты пульса от возраста) для каждой из двух групп.
190
