1) Кинематика сложного движения точки. Абсолютное, относительное и переносное движение.

Сложное движение точки (тела) – такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁).

Абсолютное - движение относительно неподвижной системы отсчета.

Относительное - движение точки отн подвижной системы отсчета.

Переносное - движение подвижной системы отсчета по отношению к неподвижной системе отсчета.

2) Теорема о сложении скоростей в сложном движении точки.

Абсолютноя скорость точки равна геометрической сумме ее переносной и относительной скоростей υ=υe+υr

Переносн скор-ть точки - линейн. Ск-ть т-ки основного звена с кот. в дан момент времени совпадает движущаяся т-ка. Относительная ск-ть т-ки в ее движении относительно основного звена Абсолют ск-ть- точки по отношению к сис-ме отсчета.

По правилу параллелограмма геом. прогрессии находится через теорему косинусов

Аналетическим способом спроецируем векторное равенство на оси координат:

3) Теорема о сложении ускорений в случае переносного поступательного движения.

Абсолютное ускорение точки равно геометрической сумме её переносного и относительного ускорений.

4) Теорема Кориолиса о сложении ускорений.

, где –ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: а) изменение модуля и направления переносной скорости точки из-за ее относительного движения; б) изменение направления относительной скорости точки из-за вращательного переносного движения.

Определение составляющих переносное и относительного ускорения : 1) В результ. вращ. Тела

h- расстояние от точки до оси вращения.

2) При криволинейном движ . p- радиус кривизны троектории.

5) Модуль и направление кориолисова ускорения.

Кореолисовым или повротным ускорением наз состовляющая обсолютного ускорения точки в сложном движении, равная удвоенному векторному произведению угловой скорости переносного вращения на относительную скорость точки

Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: а_с= 2|_ev_r|sin(_e^{^}v_r), направление вектора определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90^о в направлении вращения.

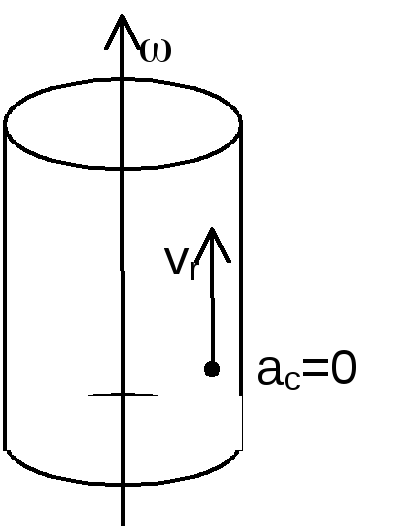
Кориолисово уск. = 0 в трех случаях: 1) _e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) v_r=0; 3) sin(_e^{^}v_r)=0, т.е. (_e^{^}v_r)=0, когда относительная скорость v_r параллельна оси переносного вращения. В случае движения в одной плоскости – угол между v_r и вектором _e = 90^о, sin90^o=1, а_с=2_ev_r