МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ

БЕЛАРУСЬ

Гомельский государственный технический университет

имени П.О.Сухого

Кафедра физики

Лабораторная работа № 2-5

Изучение температурной зависимости электрического сопротивления проводников и полупроводником.

Выполнил студент гр. Э-13 Колесников П.М.

Принял преподаватель

Курбатова Л.М.

г. Гомель, 2001

Лабораторная работа № 2-5

Тема: Изучение температурной зависимости электрического сопротивления проводников и полупроводником.

Цель работы: Изучить зависимость электрического сопротивления проводников и полупроводником от температуры, рассчитать величину энергии активации для полупроводников и величину термического коэффициента электросопротивления проводника.

Приборы и принадлежности: Сушильный шкаф, два электронных вольтметра В7-27, образцы проводов и полупроводников.

Теоретическая часть

1. Придвижении в металлах электроны проводимости испытывают соударения с ионами решетки. Между двумя последовательными соударениями, электроны движутся под действием поля с ускорением, приобретают определенную энергию. Эта энергия передается полностью или частично положительным ионам при соударениях и превращается в тепло. Причина электрического сопротивления заключается в соударениях электронов с положительными ионами решетки метала, с повышением температуры метала усиливается хаотическое движение ионов решетки, затрудняя упорядоченное движение электронов, что увеличивает сопротивление проводников. Для чистых металлов с ростом температуря сопротивление увеличивается линейно 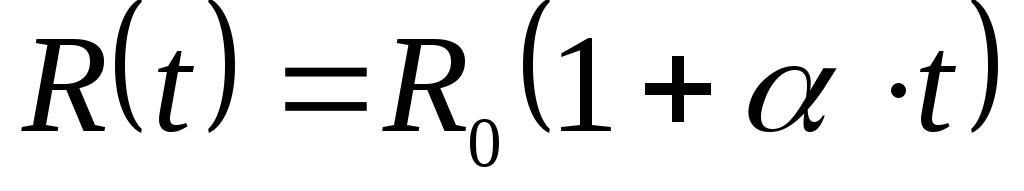, где - сопротивление при t=0⁰C; - сопротивление при t⁰С; - термодинамический коэффициент сопротивления, равный примерно 1/273.

2. При наложении внешнего электрического поля электроны приобретают дополнительное упорядоченное движение в направлении противоположном направлению поля, т. е. возникает ток.

3. Как известно, величина электропроводимости зависит от концентрации носителей заряда и их подвижности. Для полупроводников существуют такие пределы концентрации зарядов и их подвижности, что обуславливает изменение электропроводимости на 13-14 порядков выше, чем у проводников. Исследование температурной зависимости сопротивления полупроводников показало, что сопротивление полупроводников с ростом температуры резко уменьшается по экспоненциальному закону вида , где - сопротивление полупроводника при температуре T; - коэффициент, характеризующий зависимость подвижности носителя заряда от температуры; k – постоянная Больцмана; - энергия активизации полупроводника.

Ход работы.

1. Снимаем показания с электронных вольтметров (температуру и сопротивление проводника и полупроводника), все данные заносим в таблицу:

t, 0C	30	40	50	60	70	80	90	100
T, k	303	313	323	333	343	353	363	373
Rмет	1,14	1,14	1,15	1,16	1,18	1,2	1,23	1,25
Rп.п.	0,19	0,18	0,15	0,13	0,1	0,08	0,06	0,04
Ln(Rп.п.)	-1,66	-1,71	-1,9	-2,04	-2,32	-2,54	-2,81	-3,22
1/T	0,0033	0,0032	0,0031	0,003	0,0029	0,0028	0,0027	0,0026

2. Строим график температурной зависимости проводника:

По построенному графику находим сопротивления R₁ и R₂ при температуре T₁ и T₂ и по формуле определяем значение температурного коэффициента метала. При T₁=338 R₁=1,17 T₂=348 R₂=1,19

3. Строим график температурной зависимости полупроводника:

4. График зависимости сопротивления полупроводника от обратной температуры в полулогарифмическом масштабе ln(R_п.п)=f(1/T):

Выделяем на полученном графике прямолинейный участок. Определяем значение ln(R_п1) и ln(R_п2) для величин 1/T₁ и 1/T₂. По формуле находим величину энергии активации полупроводника: ln(R_п1)=-1,9, ln(R_п2)=-2,4, 1/T₁=0,00305, 1/T₂=0,002805

5. Вывод: В результате проделанной работы мы изучили температурную зависимость проводника, температурную зависимость полупроводника, определили значение температурного коэффициента метала () и величину энергии активации полупроводника ().