МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ
БЕЛАРУСЬ
Гомельский государственный технический университет
имени П.О.Сухого
Кафедра физики
Лабораторная работа № 1-4
Выполнил студент гр. Э14
Принял преподаватель
г. Гомель, 2001
Лабораторная работа № 1-4
Изучение законов сохранения импульса и энергии при ударе.
Цель работы: изучить законы сохранения импульса и энергии при упругом ударе шаров.
Теоретическая
часть:
Столкновение тел.
1.Абсолютно упругий удар, – удар при котором механическая энергия системы не изменяется (вып. Законы сохранения импульса и кинетической энергии).
Обозначим
скорости шаров с массами
и
до
удара через
и
,
после
удара – через
и
.
x
Законы сохранения имеют вид :
Решая систему, получаем:
2.Абсолютно неупругий удар – столкновение двух тел, в результате которого тела соединяются и движуться с общей скоростью (закон сохр. импульса).
x
Обозначим
скорости шаров с массами
и
до
удара через
и
,
тогда
закон сохранения импульса можно записать:
откуда получаем:
Кинетические энергии шаров до и после удара :
При абсолютно неупругом ударе происходит потеря кинетической энергии, но возрастает внутренняя энергия тела.
,
где
,
-- приведенная
масса шаров.
Ход работы:
Задание 1: Проверка закона сохранения импульса.
1.Определяем массы шаров:
2.Записываем
значение угла
,
на
который отклонился шар массой
:
|
№ |
|
|
|
|
1 |
9 |
2,25 |
7 |
|
2 |
9 |
1,75 |
6,75 |
|
3 |
9 |
2 |
7,25 |
где
,
--углы
на которые отклонялись шары после
соударений.
3.Замеряем длину подвеса шаров:
4.Определяем
скорости шаров
до
соударений,
,
--
после
соударений :
5.Определяем импульсы шаров до и после соударений и сравниваем значения:
В ходе сравнения , видим, что импульсы до и после ударов почти равны.
Задание 2: Определение коэффициента восстановления энергии и скорости для упругого удара:
1.Используя данные, полученные в задании 1, вычисляем коэффициент восстановления скорости:
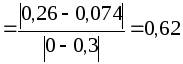
Вычисляем коэффициент восстановления энергии:
Вывод: В результате проделанной работы изучили законы сохранения импульса и энергии при упругом ударе шаров.