
3.10.1. Нормальное и тангенциальное ускорение
Направим
единичный вектор ![]() вдоль вектора скорости:
вдоль вектора скорости:

Тогда
![]()
(по правилу нахождения производной от произведения).
Первый член, нормальное ускорение,

показывает быстроту изменения направления скорости.
Второй, тангенциальное ускорение,
![]()
направлен вдоль скорости и показывает быстроту изменения ее модуля.
Направление и величину нормального ускорения найдем для частного случая равномерного движения материальной точки по окружности:

Направлен
![]() ,
при
,
при![]() ,
по вектору
,
по вектору![]() :
:
![]() .
.
 .
.
Нормальное ускорение направлено по нормали к скорости, его модуль:
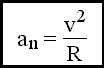 .
.
Для движения по произвольной кривой R - радиус кривизны траектории - не будет величиной постоянной.
 .
.
![]() .
.
4. Динамика материальной точки
4.1. Почему в кинематике вводят только две производные от радиус-вектора: первую - скорость
![]() .
.
и вторую - ускорение?
![]() .
.
А если
ввести некую
![]() ?
?
Можно,
но обычно не нужно. Основная задача
механики - предсказать положения тел в
любой момент времени, т.е. предсказать
вид функции
![]() для
всех изучаемых тел. Но в природе не
существует фундаментального закона,
что-либо утверждающего непосредственно
о радиус-векторе материальной точки.
для
всех изучаемых тел. Но в природе не
существует фундаментального закона,
что-либо утверждающего непосредственно
о радиус-векторе материальной точки.
Закон обнаруживается на более глубоком уровне - на уровне второй производной от радиус - вектора:
![]() -
нет закона;
-
нет закона;![]() -
нет закона;
-
нет закона;![]() -
есть закон! →
-
есть закон! → ,
см.(4.6).
Двигаясь по этой цепочке "обратным
ходом", мы можем, получив из закона
природы (второй закон Ньютона) ускорение
,
см.(4.6).
Двигаясь по этой цепочке "обратным
ходом", мы можем, получив из закона
природы (второй закон Ньютона) ускорение
![]() ,
найти сначала
,
найти сначала![]() ,
затем и
,
затем и![]() .
Поэтому обычно нет необходимости
дифференцировать
.
Поэтому обычно нет необходимости
дифференцировать![]() больше,
чем два раза.
больше,
чем два раза.
4.2. Инерциальные системы отсчета. Первый закон Ньютона Инерциальная система отсчета - это система отсчета (3.3), в которой тела, не подверженные воздействию других тел, движутся прямолинейно и равномерно. Первый закон Ньютона:
Всякое тело находится в состоянии покоя или равномерного прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
4.3.
Сила![]() - векторная величина, характеризующая
воздействие на данное тело других тел.
Величину силы можно определить опытным
путем, используя прибор для измерения
силы - динамометр.
- векторная величина, характеризующая
воздействие на данное тело других тел.
Величину силы можно определить опытным
путем, используя прибор для измерения
силы - динамометр.
4.4. Масса тела, m, - скалярная величина, являющаяся мерой инертности тела. Инертность - неподатливость действию силы, свойство тела сохранять величину и направление своей скорости, невозможность ее мгновенного изменения.
4.5. Импульс материальной точки - это вектор, равный, в механике Ньютона, произведению массы точки на ее скорость.

При v → с это определение импульса не годится. Импульс в этом случае (в теории относительности) :
 .
.
4.6. Второй закон Ньютона Скорость изменения импульса равна действующей на материальную точку результирующей силе: .
 ,
где
,
где

Из (4.5)
![]()
при m ≠ m(t)
![]() ,
,
т.к.
 (3.10),
то
(3.10),
то
![]() или
или
 .
.
4.6.1. Система си (System international)
В этой системе семь основных единиц, для них существуют эталоны.
Это единица длины - метр (м);
массы - килограмм (кг);
времени - секунда (с);
силы электрического тока - ампер (А);
температуры - Кельвин (К);
силы света - кандела (кд);
количества вещества - моль (моль).
Все остальные единицы являются производными, их размерности определяются из формул, связывающих производные величины с основными.
В механике используются первые три единицы: метр, килограмм, секунда. Отметим, что с точки зрения логики эти три единицы являются достаточными для введения производных от них величин не только в механике, но и во всей физике.
