Физика / ФИЗИКА / shpory / физика / физика_1 / Скорость

1. Скорость – это векторная величина которая определяется как быстрота движения.

Ускорение – это быстрота изменения скорости. ; ; ;

2. При криволинейном движении тело обладает двумя ускорениями : нормальным и тангенциальным. Нормальное –это движение к центру окружности. Оно показывает как меняется ускорение по направлению. ; полное ускорение

Тангенциальное – показывает как меняется скорость по величине. Если тело движется по криволинейной траектории оно обладает двумя ускорениями.

3. Вращательное движение – это движение при котором каждая точка тела движется по окружности, центры которой лежат на одной прямой, которые наз. осью врашения.

Основная характеристика вращательного движения угол поворота .Если за время t тело повернулось на угол ,то - средняя угловая скорость. Угловая скорость – это вектор (последовательность), её направление определяет правило буравчика (правило правой руки).

Мгновенная угловая скорость – это производная от угла . Угловое ускорение – производная по угловой скорости. .=рад/с². Угловое ускорение – это тоже вектор, оно направлено по оси в ту сторону, куда направлена изменение угловой скорости.

, .

4 . , продифференцировали - , еще продифференцируем - . Нормальное ускорение - .

5. Основы динамики составляют законы Ньютона, которые были сформированы в результате многочисленных экспериментов. 1 закон – Существует система отсчета , в которых тело сохраняет состояние покоя, или равномерного прямолинейного движения, если на него не действуют другие тела. Инерциальная система отсчета – система отсчетов в которой выполняется 1-вый закон Ньютона, если не выполняется неинерциальная.

6. Инертность – это все тела сопротивляются в попытке изменить своё состояние покоя или равномерного прямолинейного движения. Мерой инертности служит масса.

Сила – это мера механического воздействия одного тела на другое. 2 закон -

Ускорение приобретаемое телом, пропорционально силе действующей на него, и обратно пропорционально его массе. . Импульс – это масса умножить на скорость .

3 закон – это силы с которыми взаимодействуют два тела равные по величине и противоположны по направлению .

7. Гравитационные силы – (силы всемирного тяготения) две точки притягиваются друг другу с силой равной ,G=6,67*10^-11 Hм²/кг²- гравитационная постоянная.

Сила тяжести – сила с которой земля притягивает к себе другие тела. .

Вес тела – это сила с которой тело действует на гравитационную опору или вертикальный подвес .- если тело покоится , - если тело движется с ускорением вверх.

Невесомость – состояние тела при котором оно движется под действием силы тяжести.

Если а>g то р=0 состояние невесомости.

8. Сила упругости это сила возникшая в теле при его деформации. . k – коэффициент жесткости H/м. x – удлинение пружины.

9. Силы терния – это силы возникшие в результате движения одного тела, относительно другого. Трение бывает : внутреннее и внешнее. Внешнее – скольжение, качение, покоя. Внешнее- при движении разных тел относительно друг друга. Внутреннее – при относительном движении частиц одного и то гоже тела. Трение покоя – когда движение еще не началось. Скольжение и качение отличается типом движения. N- сила реакции опоры. - коэффициент трения скольжения.

10. Закон сохранения импульса – суммарный импульс замкнутой системы остается постоянным. .

11. Центром масс – система материальных точек наз точка С положения корой определяется формулой

12. Неинерциальные системы отсчета – это системы отсчета движущиеся относительно инерциальной системы с ускорением. Силы инерции . w – ускорение подвижной системы отсчета, относительно неподвижной.

13. Работа – физическая величина равная произведению силы на перемещение и на косинус угла между этими векторами. . Мощность это физ величина равная работе которая совершается за единицу времени. .

14. Кинетическая энергия – числена равна работе которую нужно сообщить в данную скорость. . Изменение кинетической энергии .

15. . Потенциальная энергия деформированной пружины к- коэффициент жесткости. x – удлинение пружины.

16. Консервативная сила – это сила, при которой работа совершаемая силами по перемещению тела из одной точки в другую не зависит от формы траектории, а зависит только от начального и конечного положения.(Сила тяжести, сила упругости)

Диссипативная сила: если работа зависит от формы траектории.(сила трения)

Закон сохранения механической энергии: полная механическая энергия в замкнутой системе остаётся постоянной, если внутри ее действуют только консервативные силы. ()

17. Если тело имеющее ось вращения приводится во вращение некоторой силой то моментом силы называется физическая величина равная: M=RFsin. Если l=Rsin, то M=Fl(l-плечо силы F).

Момент силы – это вектор который направлен по оси вращения: M=RF

Момент импульса – это физическая величина: L=mRsin; l=Rsin

Момент импульса – это вектор: L=Rp (p – импульс: p=m)

Если , то сделав замену: L=

Момент инерции:

Величина I=называется моментом инерции твердого тела. Он зависит от распределения массы в пространстве и является аналогом массы при вращательном движении. Тогда момент импульса твердого тела: L=I [I]=

18. Для некоторых тел(момент инерции):

Кольцо: I=m

Cтержень: I=; I=

Диск: I=

Теорема Штейнера: Если известен момент инерции , то момент инерции этого тела относительно параллельной оси, не проходящей через центр инерции равен:

=+ (где m – масса тела; x – расстояние между осями)

19. закон сохранения момента импульса(L): момент импульса замкнутой системы остаётся постоянным.(L=const; )

Основное уравнение вращательного движения: или

20.

Элементарная работа при движении по окружности: (т.к. P=A/t, то подставляем…)

21. Колебание – движение, характеризующееся повторяемостью во времени.

Собственные колебания: если они происходят без воздействия внешних сил.

Вынужденные – под действием внешних сил.

Гармонические – если колеблющаяся величина изменяется по закону sin, cos: x=Asin(), где A-амплитуда, () – фаза, - начальная фаза, - циклическая частота(=),

22. Пружинный маятник:

По 2 закону Ньютона: F=ma; ; a=x’’; Подставляем, значит: -kx=mx’’; mx’’+kx=0; x’’+kx/m=0;

23. Физический.

Тело, совершающее колебания под действием силы тяжести вокруг оси (под действием ) не проходит через центр масс. Если маятник отклонить на угол, то сила F возвратит его в исходное состояние: F=

Момент этой силы: ;

M=; значит: ; ; ; (обозначим, значит): - уравнение гармонического осциллятора.

- частота

T= ( если , то )

Математический:

Это материальная точка, с m, подвешенной на невесомой, нерастяжимой нити с длиной l;

Момент инерции:

;

T= - период

24. Если точка совершает гармонические колебания (по закону sin или cos), то скорость:

Кинетическая энергия:

Потенциальная:

Т.к. , то:

Полная энергия:

25. Сложим колебания одного направления. Точка участвует в 2 колебаниях.

№1 – с одинаковыми частотами.

(векторная диаграмма)(результат по теореме cos):

Значит фаза нового колебания: находим из треугольника:

№2 – с одинаковыми амплитудами и близкими частотами.

Значит:

x=.

26. Пусть точка участвует в 2 взаимно перпенд.колебаниях одинаковой частоты.

Преобразуем: , т.е. это основное уравнение эллипса

При

При

Если частоты колебаний не равны, но кратны друг другу, то получаются сложные кривые – фигуры Лиссажу.

27. Все реальные колебания затухают со временем. (r-коэф.сопрот.возд)

По 3 закону Ньютона:

, заменим , обозначим: . После преобразований:

Р-е:

,

где начальная амплитуда

- амплитуда затухающих колебаний

- коэф.затухания

- частота затухающих колебаний

- частота незатух.колебаний(при отсутствии сопротивления)

- декремент затухания

- логарифмический декремент затухания

- добротность

28. Вынужденные колебания – это колебания, происходящие под действием внешних сил.

Амплитуда:

Фаза:

Резонанс – явление разного возрастания A вынужденных колебаний при

29. Если в некоторой точке упругой среды возбудить колебания, то из-за связи между частицами они будут распределяться в среде. Процесс распространения – волна.

Свойства волны определяется свойствами вещества.

Поперечная – если частицы колеблются перпенд.направлению распространению волны.

Продольная – вдоль направления.Длина волны – расстояние, проходимое волной за 1 период колебаний.

Фронт волны – геометрическое место точек до которых дошли колебания.

Волновая поверхность – геометрическое место точек, колеблющихся в одной фазе.

По форме волновых поверхностей: сферические и плоские.

- уравнение плоской бегущей волны. Позволяет находить отклонение частиц в момент времени t в точке x.

29. Образование стоячих волн происходит при сложении 2 бегущих волн идущих навстречу друг другу.

= > - уравнение стоячей волны, где

- амплитуда С.В.

- длина ст.волны

Точки волны, амплитуда которых max – это пучности, а min=0.

29. Этот раздел изучат свойства и превращения тел при макроскопических процессах

(тепловых).

Статический метод: молярная физика изучает свойства и превращения тел, исходя из характера движения и взаимодействия составляющих их частиц.

Термодинамический: изучает свойства и превращения тел, не интересуясь их строение.

МКТ:

- все тела состоят из мельчайших частиц(молекулы, атомы, ионы)

- все частицы находятся в хаотическом движении

- они взаимодействуют друг с другом

32. - уравнение Клапейрона-Менд.(состояние идеального газа)

концентрация в-ва.

R – универсальная газовая постоянная:

(; постоянная Больцмана

33. Основное уравнение МКТ:

(n – концентрация; -среднеквадратичная: )

33. Функция распределения молекул по скоростям:

Закон о распределении молекул идеального газа по скоростям:

Чтобы найти max вычислим произв.и приравняем к 0:

Среднеквадрат. скор.малекул:

35. - Барометрическая формула (позволяет наход.зависимость P от h)

Если заменить => - распределение Больцмана

36. - длина свободного пробега

- среднее число столкновений молекул(где n-концентрация; V-объём; ; - площадь основания)

Физич.вакуум – такое состояние газа при котором <l> во много раз < размеров сосуда.

37. Явления переноса: явления связанные с переносом вещества, энергии и импульса(диффузия, теплопроводность, вязкость: внутреннее трение).

Диффузия – это выравнивание концентраций в смесе веществ(перенос массы)

- уравнение Фика ( - градиент(перепадов) концентрации;

D-коэф.диффузии: зависит от в-ва)

Для идеального газа:

38. Теплопроводность(перен.энергии): если в одной точке газа темп.выше, чем в другой, то молекулы, имеющие > скорости будут проникать в область, где скорость < и отдавать ; температура будет выравниваться.

Количество теплоты, перенесенное через площадь за время:

- уравнение Фурье(теплопроводности) K-коэф.теплопров.

Для газов:

39. Внутр.трение(перенос импульса):

Если 2 слоя жидкости газа движутся относительно друг друга с разными скор., то между ними возникает:

- уравнение Ньютона

S – площадь соприкосновения слоёв; - коэф.вязкости

Между слоями происходит перенос импульса.

Для газов(динамич.вязкость): ;

40. Число степеней свободы – число независимых переменных необходимых для задания положения системы в пространстве.(всего 3)

Средняя кинет.энергия молекул идеального газа:

Внутренняя энергия=сумме кинетич.и потенциальной, но у идеального газа молекулы не имеют потенц.энергии => внутр.энергия=сумме кинетических:

Изменение внутр.энергии:

41. Энергия переданная без совершения механической работы – Q-кол-во теплоты. [Дж]

1 начало термодинамики: если газ нагреть, то его внутренняя энергия увеличится, и газ расширяясь совершит работу. По закону сохр.энергии:

42. Теплоёмкость тела – кол-во теплоты, которое нужно сообщить телу, чтобы нагреть на 1 кельвин:

Удельная теплоёмкость – кол-во теплоты необходимое для нагревания 1кг. в-ва на 1кельвин: [C]=Дж/кг*к

Молярная теплоёмкость – кол-во теплоты необходимое для нагревания одного моля в-ва на 1к. [C]=Дж/моль*к

Различают:

- теплоёмкость при постоянном давлении:

- теплоёмкость при постоянном объёме

- уравнение Майера

43. Адиабатный – процесс перехода с-мы из одного состояния в другое, если он происходит без теплообмена с окружающей средой.

1 закон:

, ; преобразовав:

- уравнение Пуассона - показатель адиабаты

44. 1) - адиабатный процесс

2) - изотермический

3) - изобарный

4) () - политропический процесс

45. Процесс наз. обратимым если он происходит как прямом так и в обратном направлении, причём система проходит тоже состояние. В противном случае процесс необратимый. Процесс наз циклическим (циклом) если система возвращается в исходное состояние. Тепловой двигатель – это термодинамическая система работающая по циклу и превращающая теплоту в механическую работу. Циклом Карно наз цикл состоящий из двух изотерм и двух адиабат.

45. Физическая величина S, дифференциал которой равен dS= 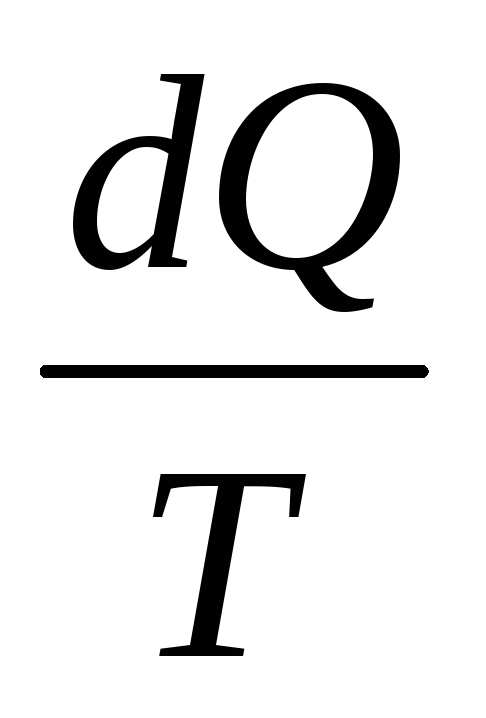наз энтропией. Изменение энтропии системы при любом переходе 12

Второе начало термодинамики : 1) Невозможен круговой процесс, единственным результатом которого является превращение теплоты , получаемой от нагревателя, в эквивалентную ей работу.