§ 3.4. Абсолютно упругий удар

Удар (соударение). Столкновение двух или более тел, при котором взаимодействие длится очень короткое время.

Центральный удар. Удар, при котором тела от удара движутся вдоль прямой, проходящей через их центры масс. Здесь рассматриваются только центральные удары.

Абсолютно упругий удар. Столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения кинетической энергии.

Прямой центральный удар. В случае прямого центрального удара векторы скоростей шаров до и после удара лежат на прямой, соединяющей их центры. Проекции векторов скорости на линию удара равны модулям скоростей. Их направления учтем знаками: положительное значение припишем движению вправо, отрицательное – движению влево. При указанных допущениях законы сохранения имеют вид

сохранение импульса , (3.17)

сохранение энергии 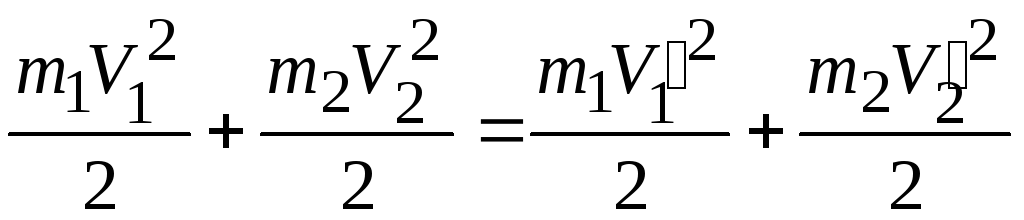. (3.18)

Решая эти уравнения, находим скорости тел после удара:

, (3.19)

, (3.20)

где – скорость центра масс шаров.

§ 3.5. Абсолютно неупругий удар

Абсолютно неупругий удар. Столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.

Согласно закону сохранения импульса,

(3.21)

(m₁ и m₂ – массы шаров, V₁ и V₂ – скорости шаров до удара, V – скорость шаров после удара). Тогда

.(3.22)

Если шары движутся навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае если массы шаров равны (m₁ = m₂), то

. (3.23)

Пример: шары из пластилина (или глины), движущиеся навстречу друг другу. В данном случае закон сохранения механической энергии не соблюдается. Вследствие деформации происходит “потеря” кинетической энергии, перешедшей в тепловую или другие формы энергии. Эту “потерю” можно определить по разности кинетической энергии тел до и после удара:

,

или с учетом (3.22) получим

, (3.24)

где – приведенная масса.

Если ударяемое тело было первоначально неподвижно (V₂ = 0), то

. (3.25)

Если m₂ >> m₁, то V << V₁ и почти вся кинетическая энергия при ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка.

§ 3.6. Графическое представление энергии

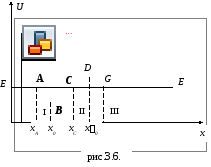
Потенциальная кривая. График зависимости потенциальной энергии от некоторого аргумента (например, координаты х: (U =U(x)). Рассматриваются только консервативные системы: в них взаимные превращения механической энергии в другие виды отсутствуют. Анализ потенциальной кривой. В общем случае потенциальная кривая может иметь довольно сложный вид, например с несколькими чередующимися максимумами и минимумами (см. рис.3.6.).

Если Е – заданная полная энергия частицы, то частица может находиться только там, где U(x)  E, т.е. в областях I и III. Переходить из области I в III и обратно частица не может, так как ей препятстсвует потенциальный барьер CDG, ширина которого равна интервалу значений х, при которых Е < U, а его высота определяется разностью U_max  E . Для того чтобы частица смогла преодолеть потенциальный барьер, ей необходимо сообщить дополнительную энергию. В области I частица с полной энергией Е оказывается «запертой» в потенциальной яме АВС и совершает колебания между точками с координатами х_А и х_С.

Так как действующая на частицу сила (U  функция только одной координаты), а условие минимума потенциальной энергии ,то в точке B – F_x = 0. При смещении частицы из положения х_о (и влево и вправо) она испытывает действие возвращающейся силы, поэтому положение х_о является положением устойчивого равновесия. Указанные условия выполняются и для точки (для U_max). Однако эта точка соответствует положению неустойчивого равновесия, так как при смещении частицы из положения появляется сила, стремящаяся удалить ее от этого положения.