Глава 3 Работа и энергия

§ 3.1. Работа и кинетическая энергия

 2 1 F ds рис.3.1. кривая L

Работой силы F на перемещении ds называется проекция FS этой силы на направление перемещения, умноженная на величину самого перемещения: dA = FS ds = Fds cos  , (3.1) где  – угол между векторами F и ds (Рис.3.1.).

Поскольку перемещение ds предполагается бесконечно малым, величина dA называется также элементарной работой в отличие от работы на конечном перемещении. Если воспользоваться понятием скалярного произведения, то можно сказать, что элементарная работа dA есть скалярное произведение силы F на перемещение ds :

dA = (F ds) . (3.2)

В общем случае, когда материальная точка, двигаясь по криволинейной траектории, проходит путь конечной длины, можно мысленно разбить путь на бесконечно малые элементы (рис.3.1.), на каждом из которых сила F может считаться постоянной, а элементарная работа может быть вычислена по формуле (3.1) или (3.2). Если сложить все эти элементарные работы и перейти к пределу, устремив к нулю длины всех элементарных перемещений, а число их – к бесконечности, то такой предел обозначается символом

(3.3)

и называется криволинейным интегралом вектора F вдоль траектории L. Этот интеграл, по определению, и дает работу силы F вдоль кривой L.

Единицей работы в системе СИ является джоуль (Дж). Джоуль есть работа силы в один ньютон на перемещение в один метр при условии, что направление силы совпадает с направлением перемещения.

Работа, отнесенная к единице времени, т.Е. Величина

, (3.4)

называется мощностью. Ее единицами является джоуль на секунду, или ватт (Вт).

Подставив в формулу (3.3) F ds = Vdt, придадим этой формуле вид

. (3.5)

Чтобы вычислить интеграл, надо знать связь между скоростью материальной точки V и ее импульсом р. По определению импульса р = mV, причем в нерелятивистской механике масса m не зависит от скорости, так что Vdp = mVdV. Итак, получим (V dV = V dV)

,

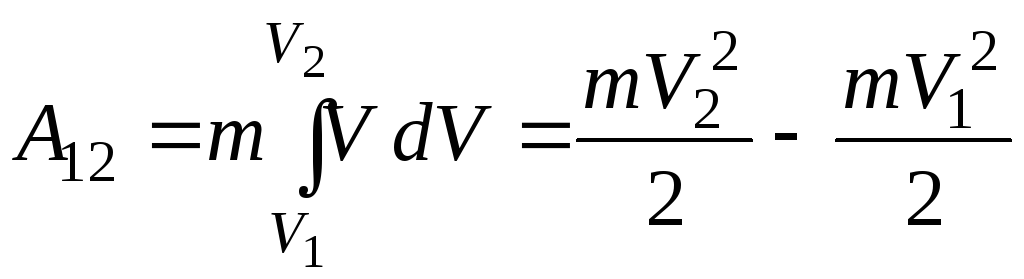где V₁ – начальная скорость, V₂ – конечная скорость точки.

Букву А мы снабдили индексами 1, 2, чтобы подчеркнуть, что речь идет о работе при перемещении материальной точки из начального положения 1 в конечное положение 2 (см. Рис.3.1.). Величина

(3.6)

называется кинетической энергиейматериальной точки. С помощью этого понятия полученный результат запишется в виде

А₁₂ = К₂ – К₁ . (3.7)

Таким образом, работа силы при перемещении материальной точки равна приращению кинетической энергии этой точки.

Полученный результат без труда обобщается на случай произвольной системы материальных точек. Кинетическая энергия системы называется сумма кинетических энергий материальных точек, из которых эта система состоит или на которые ее можно мысленно разделить.

Работа этих сил, действующих на систему материальных точек, равна приращению кинетической энергии этой системы.